Matematyka Klub 44 - Matematyka
Klub 44M - zadania VII 2012
Liga zadaniowa Wydziału Matematyki, Informatyki i Mechaniki, Wydziału Fizyki Uniwersytetu Warszawskiego i Redakcji Delty
Matematyka Klub 44 - Matematyka
Liga zadaniowa Wydziału Matematyki, Informatyki i Mechaniki, Wydziału Fizyki Uniwersytetu Warszawskiego i Redakcji Delty

Zastosowania matematyki Deltoid
Kryptografia wizualna to metoda komputerowego szyfrowania obrazów, w której do rozszyfrowania wystarczy... popatrzeć. Konkretniej, z obrazu, który chcemy zaszyfrować („obrazem” może być też napisany na kartce tekst), tworzymy dwa „pstrokate” obrazy, z których nic nie można odczytać.

Kryptografia wizualna to metoda komputerowego szyfrowania obrazów, w której do rozszyfrowania wystarczy... popatrzeć. Konkretniej, z obrazu, który chcemy zaszyfrować ("obrazem" może być też napisany na kartce tekst), tworzymy dwa "pstrokate" obrazy, z których nic nie można odczytać.
W poprzednim numerze Delty przedstawiłem trzy dowody V postulatu Euklidesa. Dla wszystkich Czytelników było jasne, że zawierają one błędy. Fakt, że mimo to każdy z nich przez pewien czas był uznany za poprawny, wskazuje na ogromny kłopot, jakim dla myślicieli – już niekoniecznie matematyków – było przyjęcie do wiadomości, że mogą istnieć dwie wykluczające się, ale poprawne, a więc w szczególności niesprzeczne teorie opisujące ten sam obiekt, w tym przypadku przestrzeń. A przecież przestrzeń, w której „odbywa się” Wszechświat, jest jedna.
Matematyka Klub 44 - Matematyka
Liga zadaniowa Wydziału Matematyki, Informatyki i Mechaniki, Wydziału Fizyki Uniwersytetu Warszawskiego i Redakcji Delty
W zawodach stopnia pierwszego wzięło udział
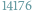 uczniów, do zawodów
stopnia drugiego zakwalifikowano 1403 uczniów, a do zawodów stopnia trzeciego –
214 uczniów.
uczniów, do zawodów
stopnia drugiego zakwalifikowano 1403 uczniów, a do zawodów stopnia trzeciego –
214 uczniów.
W zawodach stopnia pierwszego wzięło udział 1409 uczniów, do zawodów stopnia drugiego zakwalifikowano 622 uczniów, a do zawodów stopnia trzeciego – 104 uczniów. Komitet Główny Olimpiady Matematycznej na posiedzeniu w dniu 20 kwietnia br. postanowił przyznać 24 osobom tytuł laureata oraz nagrody pierwszego, drugiego, trzeciego i czwartego stopnia, zaś 3 osobom – wyróżnienie.
Matematyka Stowarzyszenie na rzecz Edukacji Matematycznej
W dniu 18 marca 2012 r. zakończyła się VII Olimpiada Matematyczna Gimnazjalistów. W zawodach pierwszego stopnia wzięło udział 14176 uczniów z 1312 szkół, w tym z kilku szkół polskich w Wilnie. Do zawodów drugiego stopnia zakwalifikowano 1403 uczniów z 627 szkół, a do zawodów trzeciego stopnia (finałowych) – 214 uczniów ze 111 szkół.
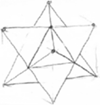
Wydaje się, że w czasach szybkich komputerów, programów graficznych i innych gadżetów nie ma sensu zajmowanie się rysunkiem odręcznym. Równie dobrze jednak można by zrezygnować z nauki pisania i tabliczki mnożenia – są przecież odpowiednie edytory i kalkulatory. Zdarza się jednak, że rozwiązując jakieś zadanie, dobrze byłoby podeprzeć naszą wyobraźnię właśnie rysunkiem, a nie ma pod ręką supernowoczesnych narzędzi.
Na IV Konferencji Stowarzyszenia Edukacji Matematycznej miałem przyjemność mówić o matematycznych zadaniach „o których nie wiedzieliście, że o nich nie wiedzieliście”. Sformułowanie to nawiązuje do niedawno przełożonej na język polski książki Johna Barrowa 100 essential things you didn’t know you didn’t know...
Od roku 2004, zwykle co dwa lata, Oddział Białostocki Polskiego Towarzystwa Matematycznego organizuje Dni Matematyki w Białymstoku. Ostatnie Dni, w roku 2011, nazywały się Podlaskie, bo kilka imprez wyszło poza Białystok.
Matematyka Klub 44 - Matematyka
Liga zadaniowa Wydziału Matematyki, Informatyki i Mechaniki, Wydziału Fizyki Uniwersytetu Warszawskiego i Redakcji Delty
Stereometria Stowarzyszenie na rzecz Edukacji Matematycznej
W zawodach I stopnia obecnej, LXIII Olimpiady Matematycznej wzięło udział 1409 uczniów, więc nieco mniej niż w poprzedniej. Jest to liczba bliska wieloletniej średniej. Do drugiego stopnia zakwalifikowano 622 uczniów. Zawody drugiego stopnia odbyły się 17 i 18 lutego.
Przemieszczając się na płaszczyźnie za pomocą ruchów „do przodu”, „do tyłu”, „w lewo” i „w prawo”, możemy w szczególności narysować kwadrat. Czy analogiczna sytuacja rozważana na zakrzywionej powierzchni zawsze pozwala na wygenerowanie kwadratu przez zakreślaną trajektorię? Rozważmy sferę, którą często wykorzystuje się w globalnym modelowaniu powierzchni Ziemi.
Oczywiście, V postulatu Euklidesa nie da się dowieść na podstawie poprzednich czterech. Niemniej jednak praktycznie każdy znaczący matematyk od V do XIX wieku taki dowód przeprowadził i dopiero jego koledzy wskazywali, w którym miejscu rozumowania użył przesłanki z czterech początkowych postulatów niewynikającej...
Planimetria Konkurs prac uczniowskich
Połączenie matematyki z religią może wydawać się nam, Europejczykom, dość zaskakujące. W Japonii jednak przez bardzo długi czas nie było niczym niezwykłym. Zjawisko to zostało zapoczątkowane w XVII wieku, kiedy władcy tego kraju podjęli decyzję o zamknięciu portów i odcięciu Japonii od reszty świata, szczególnie od Europy Zachodniej, a trwało do XIX wieku.
W fizyce szkolnej nieustannie przewijającym się motywem są dwa znane miasta: miasto A oraz miasto B. W kryptografii takimi gwiazdami są Alicja i Bob, którzy ciągle się komunikują, uwierzytelniają, a zwykle przeszkadza im w tym złowroga Ewa.

Od dwóch lat Fundacja Matematyków Wrocławskich oraz Instytut Matematyczny Uniwersytetu Wrocławskiego organizują konkurs matematycznego origami „Żuraw”. Mogą w nim startować uczniowie ze wszystkich typów szkół, a także dorośli amatorzy i profesjonalni matematycy. W odróżnieniu od innych konkursów origami w tym nie wystarczą zdolności manualne. W eliminacjach zawodnicy wykonują model matematyczny (płaski lub przestrzenny) w technice origami, natomiast w finale jest na odwrót – rozwiązują problemy dotyczące sztuki origami, używając technik matematycznych.
Matematyka Klub 44 - Matematyka
Liga zadaniowa Wydziału Matematyki, Informatyki i Mechaniki, Wydziału Fizyki Uniwersytetu Warszawskiego i Redakcji Delty
Sprawdź, Czytelniku, czy potrafisz...
Poprzedni deltoid poświęcony był osiom potęgowym, między innymi twierdzeniu, które w skrócie brzmi tak: osie potęgowe trzech okręgów przecinają się w jednym punkcie. Ciekawym jego zastosowaniem jest dowód twierdzenia Brianchona.
Planimetria Stowarzyszenie na rzecz Edukacji Matematycznej
7 stycznia 2012 roku około 1400 uczniów wzięło udział w drugim etapie VI Olimpiady Matematycznej Gimnazjalistów. Najciekawszym i jednocześnie najtrudniejszym zadaniem okazało się zadanie z planimetrii oznaczone numerem 5. Rozwiązało je niewielu uczniów, przy czym żaden z nich nie rozważył wszystkich możliwych konfiguracji. Poniżej postaramy się zadanie to dokładnie zanalizować.
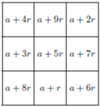
Zamieszczony w poprzednim numerze, jako zapowiedź tego numeru, widoczny obok
kwadrat magiczny jest dla
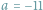 (lub
(lub
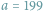 ) i
) i
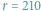 złożony
z samych liczb pierwszych.
złożony
z samych liczb pierwszych.