Małe Twierdzenie Fermata
Małe Twierdzenie Fermata ma również taki dowód...
Małe Twierdzenie Fermata ma również taki dowód...
Indukcja pozaskończona wykorzystywana jest w dowodach istnienia różnych obiektów matematycznych. Główną częścią tego typu dowodu jest definicja indukcyjna (inaczej: rekurencyjna) funkcji.
Sprawdzanie poprawności dowodów matematycznych często wymaga sporej wiedzy i ogromu nużącej pracy. O ile dochodzenie do zrozumienia istoty dowodu, czyli dlaczego dane twierdzenie matematyczne zachodzi, może sprawiać Czytelnikowi dużo satysfakcji, o tyle weryfikowanie wszystkich szczegółów dowodu jest zajęciem dość niewdzięcznym. Z tego powodu od wielu już lat trwają badania nad zaprzęgnięciem komputerów do tej żmudnej części pracy...
Twierdzenie Talesa dowieść można bez trudu...
Udowodnijmy lub obalmy twierdzenie: istnieją takie liczby niewymierne 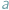 i
i 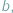 że
że 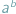 jest liczbą wymierną.
jest liczbą wymierną.
Metoda probabilistyczna gościła już na łamach Delty (np. w numerach 12/2006 i 4/2015), byłoby jednak nieprawdopodobnie głupio pominąć ją w numerze poświęconym dowodom.
Twierdzenie Pascala o równomiernym ciśnieniu gazu na ścianki naczynia pociąga za sobą twierdzenie Pitagorasa i jego uogólnienie, czyli twierdzenie kosinusów.
Zbiór wszystkich liczb rzeczywistych 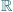 nie jest równoliczny ze zbiorem wszystkich liczb naturalnych
nie jest równoliczny ze zbiorem wszystkich liczb naturalnych 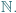

Paradoks Banacha-Tarskiego (1924 r.). Kulę można rozłożyć na skończenie wiele części, z których da się zbudować dwie takie same kule.
Matematyka Klub 44 - Matematyka
Liga zadaniowa Wydziału Matematyki, Informatyki i Mechaniki, Wydziału Fizyki Uniwersytetu Warszawskiego i Redakcji Delty
Styczniowy deltoid poświęcony był dwubarwnym mapom...
Podwojenie sześcianu to zadanie: skonstruuj odcinek 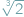 razy dłuższy od danego...
razy dłuższy od danego...
Grając w większość gier karcianych, musimy przetasować talię w taki sposób, aby ich kolejność była "jak najbardziej" losowa. Pierwszym pytaniem, na które odpowiemy sobie w tym artykule, jest pytanie o probabilistyczny sposób wyrażenia tej własności.
Tradycyjnie fraktale kojarzą nam się (często) z ładnymi rysunkami figur, które wykazują pewien zestaw cech odróżniających je od zwykłych obiektów. Nie precyzujemy tutaj uniwersalnego zestawu, gdyż sama definicja fraktala nie jest uniwersalna. W większości sytuacji chcemy, aby fraktal miał złożoną strukturę, spełniał pewne cechy samopodobieństwa oraz by nie dało się go zbyt prosto opisać geometrycznie. Mimo to często można go opisać względnie prosto pewnymi regułami rekurencyjnymi wykonywanymi na obiekcie startowym (lub zestawie takich obiektów).
Pętle na rysunku 1 przedstawiają ten sam sznurek...
Cytat z General Relativity Johna Archibalda Wheelera, który został umieszczony u góry marginesu artykułu Michała Bejgera, można przejrzyście zilustrować geometrycznie, gdy zajmiemy się przestrzenią dwuwymiarową.
Matematyka Klub 44 - Matematyka
Liga zadaniowa Wydziału Matematyki, Informatyki i Mechaniki, Wydziału Fizyki Uniwersytetu Warszawskiego i Redakcji Delty

Dlaczego w szkole tak dużo uczymy się o wielomianach? Są dwa podstawowe powody. Pierwszy z nich - całkiem zrozumiały - po prostu jest to niemal największa klasa funkcji, których wartości umiemy obliczać. Potrafimy jeszcze dzielić wartości wielomianów, ale z pozostałymi funkcjami, które występują w programie szkolnym, a później na studiach, w zasadzie mielibyśmy sporo problemów.
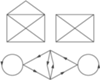
Rys. 1 (a), (b), (c). Linie oznaczone strzałkami można rysować tylko zgodnie z ich kierunkiem
Które z rysunków 1 (a), (b), (c) da się narysować bez odrywania ołówka od kartki i bez rysowania ponownie wzdłuż narysowanej już linii?
Matematyka Stowarzyszenie na rzecz Edukacji Matematycznej
W dniach 21-23 października 2016 roku w Sielpi koło Kielc odbyła się dziewiąta konferencja zorganizowana przez Stowarzyszenie na rzecz Edukacji Matematycznej. Konferencja była kolejną okazją do spotkań osób z różnych środowisk zaangażowanych w edukację matematyczną, popularyzację matematyki i pracę z młodzieżą uzdolnioną matematycznie. Do ośrodka wypoczynkowego "Łucznik" przyjechało około 160 nauczycieli matematyki i pracowników wyższych uczelni z całej Polski.
Rozważmy scenariusz, w którym wyborcy głosują na kandydatów w celu wyłonienia zwycięskiego komitetu (podzbioru kandydatów o ustalonej liczebności). Przykładami takiego scenariusza są wybory parlamentarne, wybory samorządowe, wybory do rad nadzorczych itp. W wielu przypadkach wynik takich wyborów zależy nie tylko od preferencji wyborców względem kandydatów, ale również od systemu wyborczego, czyli od metody używanej do wyłaniania zwycięzców. Różne systemy wyborcze mają także różny wpływ na późniejsze zachowanie członków wybranego komitetu.
Wojtek leżał na podłodze i czytał właśnie książkę o grafach, którą wypożyczył z biblioteki. Alicja, jego młodsza siostra, która przeglądała w tym czasie portal społecznościowy, spytała nagle...
Wyobraźmy sobie, że wewnątrz trójkąta 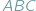 umieściliśmy trójkąt
umieściliśmy trójkąt 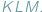 Wówczas pole
Wówczas pole 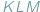 nie przekracza, oczywiście, pola
nie przekracza, oczywiście, pola 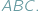 Czy możemy stwierdzić to samo o obwodach tych trójkątów? W tym przypadku słowo "oczywiście" również wydaje się uprawnione, Czytelnicy Delty z pewnością wiedzą jednak, jak łatwo o nadużycie tej formułki. Szczęśliwie w tej sytuacji nie pociągałoby to za sobą tragicznych konsekwencji, gdyż istotnie, również obwód trójkąta
Czy możemy stwierdzić to samo o obwodach tych trójkątów? W tym przypadku słowo "oczywiście" również wydaje się uprawnione, Czytelnicy Delty z pewnością wiedzą jednak, jak łatwo o nadużycie tej formułki. Szczęśliwie w tej sytuacji nie pociągałoby to za sobą tragicznych konsekwencji, gdyż istotnie, również obwód trójkąta 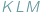 nie przekracza obwodu trójkąta
nie przekracza obwodu trójkąta 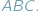
Matematyka Klub 44 - Matematyka
Liga zadaniowa Wydziału Matematyki, Informatyki i Mechaniki, Wydziału Fizyki Uniwersytetu Warszawskiego i Redakcji Delty
Dawno, dawno temu, za drugą górą, za trzecią rzeką żył sobie królewicz Leonardo pochodzący ze szlachetnego rodu Fibonaccich. No, może nie całkiem królewicz, ale piąty syn dyplomaty włoskiego. Może nie całkiem za trzecią rzeką, bo urodził się za ósmą doliną i trzynastoma bagnami, dokładniej w Pizie w 1175 roku. Zatem przynajmniej rzeczywiście żył dawno, dawno temu. Choć w pewnym sensie żyje do dzisiaj w swoich uczniach, bowiem wieść o liczbach Fibonacciego rozeszła się po świecie i szumi o nich niejeden las...