Co to jest?
Miara informacji
Jak wiadomo, komputery traktują wszystkie dane, na których działają, jako ciągi
bitów, z których każdy może mieć dwie wartości (0 lub 1). Przykładowo,
ten tekst jest zapisany w ten sposób, że każdej z liter i pozostałych znaków
odpowiada ciąg 8 bitów. Daje to
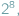 czyli 256 możliwości, co
w zupełności wystarcza do zapisania wszystkich potrzebnych znaków. Jednak
w rzeczywistości różnych znaków występujących w tekście jest mniej.
Problem jest więc taki: jak zapisać tekst tak, żeby na każdą jego literę
przypadało jak najmniej bitów?
czyli 256 możliwości, co
w zupełności wystarcza do zapisania wszystkich potrzebnych znaków. Jednak
w rzeczywistości różnych znaków występujących w tekście jest mniej.
Problem jest więc taki: jak zapisać tekst tak, żeby na każdą jego literę
przypadało jak najmniej bitów?

Załóżmy dla przykładu, że w naszym alfabecie są 3 litery: A, B i C. Najprostszy sposób kodowania jest następujący – każdą z liter kodujemy ciągiem dwóch bitów, powiedzmy A = 01, B = 10, C = 11. Ten sposób zapisu (nazwijmy go (1)) daje 2 bity na każdą literę.
Łatwo zauważyć, że powyższy kod da się poprawić: jeśli pierwszym
bitem kodu litery jest 0, to już nie musimy pisać drugiego bitu 1. Jeśli
założymy, że nasze litery występują tak samo często, to okaże się, że nasz
nowy sposób zapisu (2) używa
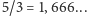 bitów na każdą
literę (co trzecia litera wymaga tylko jednego bitu). Są też możliwe
bardziej skomplikowane kody. Czytelnikowi zostawiamy kodowanie (3)
o „efektywności”
bitów na każdą
literę (co trzecia litera wymaga tylko jednego bitu). Są też możliwe
bardziej skomplikowane kody. Czytelnikowi zostawiamy kodowanie (3)
o „efektywności”
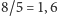 bitów na literę (podpowiedź: kodujemy
bloki 5 znaków).
bitów na literę (podpowiedź: kodujemy
bloki 5 znaków).
Teraz zwróćmy uwagę na powyższe założenie: litery występują tak samo
często. A co, jeśli, na przykład, litera A występuje z prawdopodobieństwem
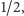 a B i C z prawdopodobieństwem
a B i C z prawdopodobieństwem
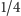 ? W sposobach
zapisu (1) i (3) nic się nie zmienia, ale sposób (2) jest teraz w stanie
używać średnio tylko
? W sposobach
zapisu (1) i (3) nic się nie zmienia, ale sposób (2) jest teraz w stanie
używać średnio tylko
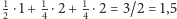 bitów na
literę!
bitów na
literę!
Jaka jest najmniejsza możliwa średnia liczba bitów potrzebnych do zapisania ciągu znaków, które występują (niezależnie) z podanym rozkładem prawdopodobieństwa? Odpowiedzi na to pytanie dostarcza teoria informacji Shannona: najmniejszą możliwą średnią liczbą bitów na jeden znak jest entropia rozkładu prawdopodobieństwa, zadana wzorem

gdzie
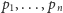 są prawdopodobieństwami kolejnych znaków.
są prawdopodobieństwami kolejnych znaków.
Przykładowo, entropia naszego pierwszego rozkładu (3 litery z równym
prawdopodobieństwem) wynosi
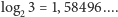 (Jeśli wymyślony
przez Czytelnika sposób kodowania 5 znaków w 8 bitach jest taki sam,
jak Autora, to łatwo go poprawiać, zbliżając się do granicy.) Entropia
naszego drugiego rozkładu ( A występuje 2 razy częściej) to
(Jeśli wymyślony
przez Czytelnika sposób kodowania 5 znaków w 8 bitach jest taki sam,
jak Autora, to łatwo go poprawiać, zbliżając się do granicy.) Entropia
naszego drugiego rozkładu ( A występuje 2 razy częściej) to
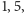 czyli nasz sposób kodowania jest optymalny. Czytelnikowi zostawiamy
obliczenie entropii rozkładu, w którym są dwie litery, A i B, przy czym
B występuje bardzo rzadko – powiedzmy, raz na
czyli nasz sposób kodowania jest optymalny. Czytelnikowi zostawiamy
obliczenie entropii rozkładu, w którym są dwie litery, A i B, przy czym
B występuje bardzo rzadko – powiedzmy, raz na
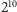 liter – i znalezienie
odpowiedniego sposobu kodowania, który pozwoli nam się zbliżyć do
otrzymanej entropii, np. wymagającego średnio 12 bitów na
liter – i znalezienie
odpowiedniego sposobu kodowania, który pozwoli nam się zbliżyć do
otrzymanej entropii, np. wymagającego średnio 12 bitów na
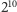 znaków.
znaków.
Entropię można rozumieć jako pewnego rodzaju miarę informacji, w naszym przypadku informacji niesionej przez 1 znak w naszym alfabecie. A teoria informacji, poza omówioną wyżej kompresją, ma również zastosowanie w innych dziedzinach informatyki (kryptografia – jak zaszyfrować tekst, by osoba podglądająca nie dostała na jego temat żadnej informacji; generowanie liczb pseudolosowych) i nie tylko (np. fizyka, badanie języka naturalnego)...