Rys. 1

Rys. 2

Rysunek 2 ukazuje (w różnych pozach) zajączka, utworzonego z tych klocków.

Oczywiście, pole kwadratu jest równe polu zajączka, ściślej, wielokąta w kształcie zajączka. Dlaczego? Ponieważ obie figury składają się z przystających części, które w każdej z nich stykają się tylko brzegami. Wiemy, że figury przystające mają równe pola, oraz że jeśli figura składa się z mniejszych figur, które stykają się tylko brzegami, to pole całej figury jest sumą pól owych mniejszych figur składowych.

Można ten fakt wyrazić inaczej: kwadrat i zajączek mają równe pola, gdyż pocięliśmy kwadrat na kawałki, z których ułożyliśmy zajączka. Nasuwa się w takim razie naturalne pytanie odwrotne: czy, mając dwie figury o równych polach, możemy pociąć jedną z nich na kawałki, tak aby można z nich było złożyć drugą figurę?

Rys. 3

Na początek spróbujmy naszych sił na dwóch prostokątach o równych polach, ale różnych bokach (rysunek 3): 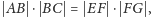przy czym 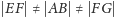(więc i 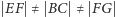 ). Poprowadźmy odcinek łączący lewy górny wierzchołek 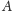pierwszego prostokąta z prawym dolnym wierzchołkiem 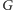drugiego prostokąta. Oznaczając odpowiednie punkty przecięcia tak jak na rysunku 3, stwierdzamy, że trójkąty 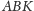i 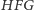 są przystające (Dlaczego? Tu może się przydać warunek równości pól, a nawet znajomość twierdzenia Talesa). Przesuwając zatem ten drugi wzdłuż odcinka 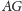(a trójkąt 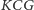na przystający do niego trójkąt 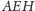), pokryjemy cały prostokąt 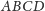kawałkami składającymi się na prostokąt

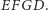
Rys. 4

Rys. 5

Jest tylko jeden szkopuł. Przecież nie zawsze odcinek 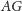przetnie dolny prostokąt z lewej strony punktu 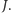Aby tak było, musi być spełniony warunek 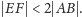Ale cóż prostszego, jak pociąć prostokąt, który tego warunku nie spełnia, na taki, który go spełnia! Wystarczy powtarzać cięcie pokazane na rysunku 4 aż do skutku.

Tak więc każdy prostokąt można tak pociąć, żeby z kawałków złożyć dowolny inny prostokąt o tym samym polu.

Możemy teraz zająć się dowolnymi wielokątami. Zapewne Czytelnik zgodzi się, że jeśli potrafimy pociąć każdy z dwóch wielokątów o tym samym polu na kawałki, z których można złożyć jeden (siłą rzeczy, taki sam dla obu) kwadrat, to potrafimy także pociąć jeden z tych wielokątów, tak by z otrzymanych kawałków złożyć drugi. Zajmiemy się zatem pocięciem wielokąta na kwadrat. Zauważmy, że:
1. każdy wielokąt można pociąć na trójkąty (rysunek 5);
2. każdy trójkąt można pociąć na kawałki, z których da się ułożyć prostokąt (rysunek 6)...
3. ...a każdy prostokąt można pociąć tak, by złożyć z niego dowolny inny prostokąt o tym samym polu – na przykład kwadrat (rysunek 7).

Rys. 6

Rys. 7

Rys. 8

W ten sposób udało nam się pokroić wielokąt, od którego zaczęliśmy zabawę, na pewną liczbę kwadratów o łącznym polu równym polu tego wielokąta. Chcieliśmy jednak otrzymać jeden kwadrat. Przywołajmy więc na pomoc twierdzenie Pitagorasa, które pozwala z dwóch kwadratów zrobić jeden o tym samym polu. Jak? Pokazuje to rysunek 8.

Mamy zatem brakujące ogniwo:
4. z otrzymanych kwadratów można złożyć jeden kwadrat, którego pole jest równe polu wyjściowego wielokąta.

Nazwijmy dwa wielokąty równoważnymi przez pocięcie, jeśli jeden z nich można pociąć na kawałki, z których można złożyć drugi. Udowodniliśmy następujące twierdzenie, znane od początków XIX wieku.

Chciałoby się powiedzieć: nic bardziej naturalnego. Jakże mogłoby być inaczej? Okazuje się jednak, że problem znacznie się komplikuje, gdy przejdziemy do przestrzeni trójwymiarowej. W początkach XX wieku wykazano, że istnieją bryły trójwymiarowe (na przykład, dwa czworościany) o równych objętościach, takie że żadnej z nich nie można otrzymać z drugiej przez pocięcie (tym razem, na „kawałki” trójwymiarowe). Ale to już zupełnie inna sprawa (patrz artykuł Pole i objętość).

---