Co to jest?
Pole i objętość
W numerze poświęconym mierze (8/2008) nie sposób pominąć tych pierwszych, czyli zwykłych miar geometrycznych (zważmy, że geometria ma miarę w swojej nazwie).Wydaje się, że wiemy o nich wszystko, bo przecież stykaliśmy się z nimi niemal od zerówki. Okazuje się jednak, że i na ich temat można postawić pytania o nieoczywistych odpowiedziach.
Rozważymy tu dwa takie pytania. Pierwsze z nich to:
Czy polem prostokąta musi być iloczyn długości jego boków?
Pisząc szerzej: czy można byłoby, bez rezygnacji z naturalnych własności miary, tak zdefiniować pole, by przyjmowało ono jakieś inne wartości? W oczywisty sposób to samo pytanie można postawić odnośnie objętości prostopadłościanu. Może od razu spiszmy te naturalne własności miary.
- I
- Figury przystające mają równe miary.
- II
- Jeśli dwie figury mają wspólny co najwyżej brzeg, to miara ich sumy jest równa sumie ich miar.
- III
- Miara kostki jednostkowej (kwadratu, sześcianu) jest równa 1.
- IV
- Miara każdej figury jest nieujemna.
W szkole poznajemy wzory na miary różnych figur płaskich i przestrzennych. Drugie pytanie to:
Czy do ścisłego obliczania pól wielokątów i objętości wielościanów konieczna jest jakaś wyższa matematyka?
Wyrażając się precyzyjniej: czy odpowiednie wzory można uzyskać elementarnie, to jest bez użycia jakichś pojęć związanych z nieskończonością (ciągu, szeregu, granicy itp.)?
Dla niedoceniających tych pytań dodajmy, że pełne odpowiedzi na nie matematycy uzyskali na początku XX wieku, czyli dopiero sto lat temu. Droga wiodła przez równania funkcyjne.
Znakomity artykuł o równaniach funkcyjnych autorstwa Marka Kuczmy zamieściliśmy w Delcie 1(37)1977; w tym tekście jest wiele zapożyczeń z tego artykułu.
Równanie Cauchy’ego
W badaniu problemów związanych z miarą kluczową rolę odgrywa równanie funkcyjne, zwane równaniem Cauchy’ego. Równanie funkcyjne to problem, w którym poszukujemy nie liczby, ale funkcji spełniającej określone warunki. W przypadku równania Cauchy’ego chodzi o następujący warunek:
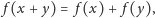 | (1) |
dla dowolnych rzeczywistych
 i
i
Oczywiście, każdy bez trudu wskaże rozwiązanie tego równania: są to
funkcje postaci
 dla dowolnej stałej
dla dowolnej stałej
 Augustyn Cauchy,
który odkrył znaczenie tego równania w teorii miary, zauważył, iż nie umie
odpowiedzieć na pytanie, czy jest to rozwiązanie jedyne. Odpowiedź na takie
pytanie przyszła dopiero w 1903 roku, a do jej sformułowania potrzebne były
nieistniejące w czasach Cauchy’ego (pierwsza połowa XIX wieku) pojęcia
matematyczne.
Augustyn Cauchy,
który odkrył znaczenie tego równania w teorii miary, zauważył, iż nie umie
odpowiedzieć na pytanie, czy jest to rozwiązanie jedyne. Odpowiedź na takie
pytanie przyszła dopiero w 1903 roku, a do jej sformułowania potrzebne były
nieistniejące w czasach Cauchy’ego (pierwsza połowa XIX wieku) pojęcia
matematyczne.
Zacznijmy rozwiązywać to równanie. Bez trudu stwierdzamy, że

Podobnie, indukcyjnie dowodzimy dla dowolnego
 że
że
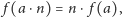 bo
bo

Dalej
 bo
bo

Wreszcie
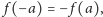 bo
bo

Podsumowując, dla dowolnej liczby wymiernej
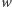 (i dowolnej liczby
rzeczywistej
(i dowolnej liczby
rzeczywistej
 ) mamy więc
) mamy więc
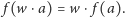 | (2) |
Oznaczając
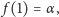 mamy
mamy
 | (3) |
Okazuje się jednak, że w tym miejscu trop się kończy – nie ma sposobu, by na
tej podstawie określić konkretną wartość
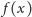 dla niewymiernego
dla niewymiernego
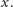
Możemy jednak myśleć tak: oznaczmy
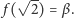 Wówczas na
mocy (2) otrzymamy
Wówczas na
mocy (2) otrzymamy
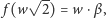 co więcej – wobec (1) – dla
dowolnych wymiernych
co więcej – wobec (1) – dla
dowolnych wymiernych
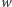 i
i


Oczywiście, dla
 otrzymamy zwykłą funkcję liniową, ale nie
musimy czynić takiego założenia –
otrzymamy zwykłą funkcję liniową, ale nie
musimy czynić takiego założenia –
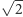 nie jest liczbą wymierną, więc
nie nastąpi kolizja w warunkiem (3). Co więcej, postępowanie to możemy
kontynuować, deklarując kolejno wartości funkcji
nie jest liczbą wymierną, więc
nie nastąpi kolizja w warunkiem (3). Co więcej, postępowanie to możemy
kontynuować, deklarując kolejno wartości funkcji
 dla nowych
wartości – nowych, to znaczy takich, których nie da się uzyskać przez
kombinację liniową liczb, dla których wartości funkcji zadeklarowaliśmy
już wcześniej (w powyższym przypadku kolejną liczbą, dla której
obierzemy dowolnie wartość funkcji
dla nowych
wartości – nowych, to znaczy takich, których nie da się uzyskać przez
kombinację liniową liczb, dla których wartości funkcji zadeklarowaliśmy
już wcześniej (w powyższym przypadku kolejną liczbą, dla której
obierzemy dowolnie wartość funkcji
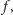 musi być liczba niedająca się
przedstawić w postaci
musi być liczba niedająca się
przedstawić w postaci
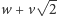 dla wymiernych
dla wymiernych
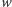 i
i
 np.
np.
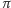 ).
).
Powstaje pytanie, czy postępowanie to daje się rozszerzyć tak, by określić
wartości
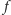 dla wszystkich liczb rzeczywistych. Odpowiedź nie jest
oczywista, bo przez kolejne przyłączanie coraz nowych liczb nie da się dojechać
„do końca” (liczb rzeczywistych jest nieprzeliczalnie wiele). Jednak silne środki
teorii mnogości (np. pewnik wyboru) pozwalają na taką operację – wykonał ją
jako pierwszy Georg Hamel (ciekawych odsyłam do hasła baza Hamela). Nam
jednak dalej wystarczą rozwiązania równania (1) uzyskane taką metodą, jak dla
liczb postaci
dla wszystkich liczb rzeczywistych. Odpowiedź nie jest
oczywista, bo przez kolejne przyłączanie coraz nowych liczb nie da się dojechać
„do końca” (liczb rzeczywistych jest nieprzeliczalnie wiele). Jednak silne środki
teorii mnogości (np. pewnik wyboru) pozwalają na taką operację – wykonał ją
jako pierwszy Georg Hamel (ciekawych odsyłam do hasła baza Hamela). Nam
jednak dalej wystarczą rozwiązania równania (1) uzyskane taką metodą, jak dla
liczb postaci
 użytą tylko skończoną liczbę razy, czyli
określone tylko dla niektórych liczb. Wspomnijmy, iż okazało się, że
wszystkie rozwiązania równania Cauchy’ego, poza liniowym, są bardzo
paskudnymi funkcjami: nie są ciągłe, ani w żadnym przedziale monotoniczne
itd.
użytą tylko skończoną liczbę razy, czyli
określone tylko dla niektórych liczb. Wspomnijmy, iż okazało się, że
wszystkie rozwiązania równania Cauchy’ego, poza liniowym, są bardzo
paskudnymi funkcjami: nie są ciągłe, ani w żadnym przedziale monotoniczne
itd.
Pole prostokąta

Rys. 1
Z podanej na początku własności I miary wynika, że pole prostokąta jest
funkcją długości jego boków (bo gdy dwa prostokąty mają równe boki, to są
przystające). Oznaczmy tę funkcję przez
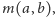 gdzie
gdzie
 i
i
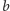 to długości boków. Ponieważ podział prostokąta odcinkiem równoległym do
jego boków (Rys. 1) daje nam dwa prostokąty, więc mamy – na mocy II –
równanie funkcyjne
to długości boków. Ponieważ podział prostokąta odcinkiem równoległym do
jego boków (Rys. 1) daje nam dwa prostokąty, więc mamy – na mocy II –
równanie funkcyjne

Ustalmy na pewien czas
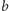 i oznaczmy
i oznaczmy
 Mamy
zatem
Mamy
zatem

– funkcja
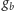 spełnia równanie Cauchy’ego. Wobec tego możemy
skorzystać z uzyskanych wyżej wzorów: mamy dla wymiernego
spełnia równanie Cauchy’ego. Wobec tego możemy
skorzystać z uzyskanych wyżej wzorów: mamy dla wymiernego
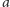

Powtarzając rozumowanie ze wspomnianego artykułu Marka Kuczmy,
rozważmy funkcję
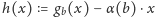 – wykażemy, że jest ona
stała i dla każdego
– wykażemy, że jest ona
stała i dla każdego
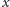 równa 0.
równa 0.
-

-
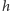 spełnia równanie Cauchy’ego:
spełnia równanie Cauchy’ego:
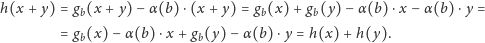
-
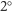
-
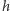 jest okresowa z okresem
jest okresowa z okresem
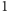 :
:
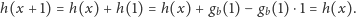
-
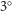
-
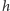 jest ograniczona z dołu; tu skorzystamy z niewykorzystanej dotąd
własności IV – w naszych oznaczeniach głosi ona, że dla
jest ograniczona z dołu; tu skorzystamy z niewykorzystanej dotąd
własności IV – w naszych oznaczeniach głosi ona, że dla
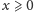 mamy
mamy
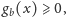 w szczególności
w szczególności
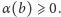 Na mocy
Na mocy
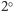 wystarczy rozpatrzyć wartości przyjmowane przez funkcję
w przedziale
wystarczy rozpatrzyć wartości przyjmowane przez funkcję
w przedziale
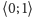 :
:
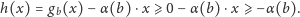
-
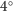
- Dla każdego
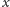 jest
jest
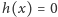 . Przypuśćmy, że znaleźliśmy
w przedziale
. Przypuśćmy, że znaleźliśmy
w przedziale
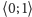 taką liczbę
taką liczbę
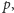 że
że
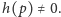 Zatem
Zatem
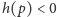 lub
lub
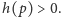 W pierwszym przypadku zauważamy,
że wobec
W pierwszym przypadku zauważamy,
że wobec
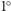 i (3) mamy
i (3) mamy
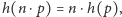 co pozwala przez
dobór odpowiednio dużego
co pozwala przez
dobór odpowiednio dużego
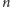 uczynić tę liczbę dowolnie
małą, co jest sprzeczne z
uczynić tę liczbę dowolnie
małą, co jest sprzeczne z
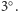 W drugim przypadku zauważmy,
że wówczas
W drugim przypadku zauważmy,
że wówczas
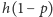 jest mniejsze od zera, bowiem, wobec
jest mniejsze od zera, bowiem, wobec

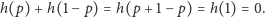
Powtarzając poprzednie rozumowanie, stwierdzamy, że teraz
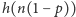 może być dowolnie małe. Zatem w każdej
sytuacji dochodzimy do sprzeczności, czyli nasze przypuszczenie
było błędne – funkcja
może być dowolnie małe. Zatem w każdej
sytuacji dochodzimy do sprzeczności, czyli nasze przypuszczenie
było błędne – funkcja
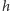 jest stale zerem, skąd mamy wniosek,
że
jest stale zerem, skąd mamy wniosek,
że

czyli dla dowolnego
 mamy
mamy
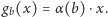

Rys. 2
Powróćmy do prostokąta. Wiemy teraz, że jego pole to

Skorzystajmy z tego, że prostokąt można podzielić na dwa prostokąty również odcinkiem równoległym do drugiej pary boków (Rys. 2). Wtedy będzie

czyli

Biorąc np.
 otrzymujemy
otrzymujemy

– funkcja
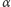 spełnia równanie Cauchy’ego! Wobec tego stosuje się do niej
przeprowadzone przed chwilą rozumowanie, co daje, dla pewnej stałej
spełnia równanie Cauchy’ego! Wobec tego stosuje się do niej
przeprowadzone przed chwilą rozumowanie, co daje, dla pewnej stałej
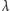

Ostatecznie więc wykazaliśmy, że musi być

Pole wielokąta, objętość wielościanu
W Małej Delcie jest dowód, że dowolny wielokąt można pociąć na części, z których ułoży się prostokąt (a nawet kwadrat) – mówimy, że dowolny wielokąt jest równoważny przez pocięcie z prostokątem. Stąd sposób obliczania pola dowolnego wielokąta jest wyznaczony jednoznacznie. Powstaje pytanie, czy można dowolny wielościan pociąć na skończoną liczbę mniejszych wielościanów, z których ułoży się prostopadłościan. Metody takiej nie przekazali nam Starożytni, ale i potem nie umieliśmy jej znaleźć, aż w 1900 roku David Hilbert umieścił pytanie, czy to w ogóle da się zawsze wykonać, w rzędzie 23 najważniejszych problemów na nadchodzący wiek XX. Odpowiedź przyszła szybko – jeszcze w tym samym 1900 roku Max Dehn udowodnił, że nie jest to możliwe.
Dokładniej, Dehn wskazał, które pary wielościanów nie są równoważne przez pocięcie. Pięćdziesiąt dziewięć lat później Jean Paul Sydler uzupełnił ten dowód, wskazując, że wszystkie inne pary już są równoważne przez pocięcie. Okazuje się, że również w tej sprawie interweniuje równanie Cauchy’ego.
Kluczem do sprawy jest niezmiennik Dehna. Dla dowolnego wielościanu
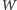 obliczamy go tak. Numerujemy wszystkie jego krawędzie
obliczamy go tak. Numerujemy wszystkie jego krawędzie
 (od 1
do
(od 1
do
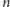 ) i tym samym numerem oznaczamy kąty dwuścienne
) i tym samym numerem oznaczamy kąty dwuścienne
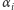 przy
tych ścianach. Bierzemy następnie jakąś funkcję
przy
tych ścianach. Bierzemy następnie jakąś funkcję
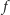 spełniającą
równanie Cauchy’ego i na dodatek spełniającą warunek
spełniającą
równanie Cauchy’ego i na dodatek spełniającą warunek
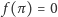 (a więc
także
(a więc
także
 dla dowolnej liczby wymiernej
dla dowolnej liczby wymiernej
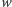 ) – taką funkcję
nazywamy funkcją Dehna. Niezmiennik Dehna dla funkcji
) – taką funkcję
nazywamy funkcją Dehna. Niezmiennik Dehna dla funkcji
 to
liczba
to
liczba

Twierdzenie (Dehna). Jeśli wielościany są równoważne przez pocięcie, to ich wszystkie niezmienniki Dehna są równe (wszystkie, to znaczy dla dowolnej funkcji Dehna).
Na pomysł takiego niezmiennika wpaść jest trudno, natomiast udowodnić twierdzenie Dehna już trudno nie jest.
Wystarczy wykazać, że wartość dowolnie ustalonego niezmiennika
Dehna dla wielościanu
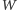 jest równa sumie tych samych
niezmienników wielościanów, na które go potniemy. W tym celu
rozważmy wszystkie krawędzie wszystkich wielościanów uzyskanych
z pocięcia. Niektóre z nich (niech taka będzie np. krawędź
jest równa sumie tych samych
niezmienników wielościanów, na które go potniemy. W tym celu
rozważmy wszystkie krawędzie wszystkich wielościanów uzyskanych
z pocięcia. Niektóre z nich (niech taka będzie np. krawędź
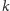 z wielościanów
z wielościanów
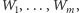 gdzie kąty dwuścienne przy niej to
odpowiednio
gdzie kąty dwuścienne przy niej to
odpowiednio
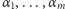 ) znajdowały się we wnętrzu wielościanu
) znajdowały się we wnętrzu wielościanu
 – jeśli tak, to teraz w sumie niezmienników
– jeśli tak, to teraz w sumie niezmienników
 nie wystąpi,
bo
nie wystąpi,
bo

– przecież ta krawędź była „otoczona” wielościanem
 Podobnie
nie wystąpi w sumie niezmienników żadna nowa krawędź, która leżała
we wnętrzu ścian wielościanu
Podobnie
nie wystąpi w sumie niezmienników żadna nowa krawędź, która leżała
we wnętrzu ścian wielościanu
 – tutaj kąty zsumują się do
– tutaj kąty zsumują się do
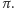 Tak więc w sumie niezmienników Dehna wielościanów, na jakie pocięliśmy
wielościan
Tak więc w sumie niezmienników Dehna wielościanów, na jakie pocięliśmy
wielościan
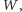 wystąpią tylko fragmenty krawędzi wielościanu
wystąpią tylko fragmenty krawędzi wielościanu
 przy czym (rozumujemy podobnie jak poprzednio) przy każdym
takim fragmencie
przy czym (rozumujemy podobnie jak poprzednio) przy każdym
takim fragmencie
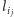 (gdzie, powiedzmy,
(gdzie, powiedzmy,
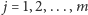 ) krawędzi
) krawędzi
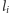 wystąpi po zsumowaniu funkcja całego kąta
wystąpi po zsumowaniu funkcja całego kąta
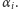 Będziemy więc
mieli
Będziemy więc
mieli

Ale przecież niezmiennik Dehna wielościanu
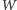 to właśnie suma
takich wyrażeń.
to właśnie suma
takich wyrażeń.

Rys. 3
Tak więc, jeśli znajdziemy taki niezmiennik Dehna, który przyjmuje inną
wartość dla wielościanu
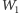 niż dla wielościanu
niż dla wielościanu
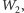 będzie to dowód, że nie są one równoważne przez pocięcie. A oto
przykład: czworościan
będzie to dowód, że nie są one równoważne przez pocięcie. A oto
przykład: czworościan
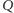 z rysunku 3 (naroże sześcianu) nie jest
równoważny przez pocięcie z żadnym prostopadłościanem. Udowodnimy
to.
z rysunku 3 (naroże sześcianu) nie jest
równoważny przez pocięcie z żadnym prostopadłościanem. Udowodnimy
to.
Najpierw zauważmy, że wszystkie niezmienniki Dehna dla prostopadłościanu
są równe 0 – istotnie, wszystkie kąty dwuścienne prostopadłościanu są
proste, czyli równe
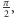 a dla każdej funkcji Dehna
a dla każdej funkcji Dehna
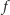 mamy
mamy
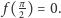 Wystarczy więc wskazać taki niezmiennik, który dla
Wystarczy więc wskazać taki niezmiennik, który dla
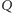 przyjmuje wartość niezerową. Niezmienniki
przyjmuje wartość niezerową. Niezmienniki
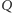 mają
postać
mają
postać

gdzie
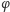 to kąt dwuścienny przy dłuższych krawędziach czworościanu.
Powstaje wobec tego pytanie, czy istnieje taka funkcja Dehna, która dla
to kąt dwuścienny przy dłuższych krawędziach czworościanu.
Powstaje wobec tego pytanie, czy istnieje taka funkcja Dehna, która dla
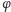 jest różna od zera.
jest różna od zera.
W części poświęconej równaniu Cauchy’ego stwierdziliśmy, że
wartość funkcji
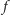 możemy obrać dowolnie wtedy i tylko wtedy,
gdy
możemy obrać dowolnie wtedy i tylko wtedy,
gdy
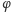 nie jest wymierną wielokrotnością
nie jest wymierną wielokrotnością
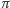 (bo na razie
tylko dla wymiernych wielokrotności
(bo na razie
tylko dla wymiernych wielokrotności
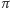 mamy zadane wartości
mamy zadane wartości
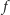 ).
).
Okazuje się, że spostrzeżenie (które zapewne nie sprawi kłopotu
Czytelnikowi), iż
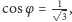 wystarcza, aby to udowodnić. Najpierw
zauważmy, że:
wystarcza, aby to udowodnić. Najpierw
zauważmy, że:
Fakt.
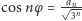 , gdzie
, gdzie
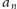 jest liczbą całkowitą niepodzielną
przez
jest liczbą całkowitą niepodzielną
przez
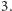
Dowód. Dowód jest indukcyjny. Dla
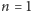 zgadza się:
zgadza się:
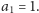 Dla
Dla
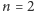 mamy
mamy

czyli też dobrze:
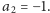 Teraz krok indukcyjny: ze znanego wzoru
mamy
Teraz krok indukcyjny: ze znanego wzoru
mamy

a wobec tego

a więc też dobrze – mianownik się zgadza, a liczba
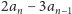 nie
dzieli się przez 3, skoro
nie
dzieli się przez 3, skoro
 się nie dzieli.
się nie dzieli.
Teraz już łatwo dowodzimy, że
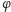 nie jest wymierną wielokrotnością
nie jest wymierną wielokrotnością
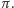 Gdyby bowiem było przeciwnie, to znaczy gdyby dla całkowitych
Gdyby bowiem było przeciwnie, to znaczy gdyby dla całkowitych
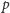 i
i
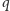 było
było

to mielibyśmy

co jest niemożliwe, bo
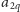 przez 3 się nie dzieli.
przez 3 się nie dzieli.

Rys. 4
Zatem możemy wybrać sobie funkcję Dehna
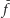 przyjmującą dowolnie
obraną przez nas wartość dla
przyjmującą dowolnie
obraną przez nas wartość dla
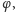 np. 1. Otrzymamy wówczas
np. 1. Otrzymamy wówczas
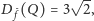 co wobec twierdzenia Dehna dowodzi, że nie da
się pociąć
co wobec twierdzenia Dehna dowodzi, że nie da
się pociąć
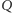 na takie wielościany, z których da się uskładać
prostopadłościan.
na takie wielościany, z których da się uskładać
prostopadłościan.
Morał z tego taki, że jeśli ktoś nam pokazuje sposób na uzyskanie wzoru
na objętość czworościanu
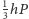 bez jakiegoś przejścia graniczmego,
to nas oszukuje (choć, być może, robi to bardzo sprytnie).
bez jakiegoś przejścia graniczmego,
to nas oszukuje (choć, być może, robi to bardzo sprytnie).
Twierdzenie (Sydlera). Jeśli wielościany mają wszystkie niezmienniki Dehna równe, to są równoważne przez pocięcie.
Nie będziemy go dowodzili, ale proponujemy Czytelnikowi wynikające z niego zadania.
- 1.
- Wykazać, że czworościan z rysunku 4 jest równoważny przez pocięcie z prostopadłościanem.
- 2.
- Znaleźć odpowiedni rozkład.
- 3.
- Wykazać, że każdy graniastosłup jest równoważny przez pocięcie z prostopadłościanem (można analitycznie, ale można też sprytnie wykorzystać twierdzenie Bolyaia–Gerwiena z Małej Delty).