Mała Delta
Równanie Pitagorasa
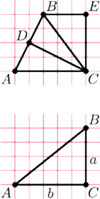
Pomysł tego artykułu powstał na lekcji matematyki w I klasie gimnazjum.
Rozwiązywałem z uczniami zadanie z podręcznika wydanego przez Gdańskie
Wydawnictwo Oświatowe: który z narysowanych trójkątów jest przystający
do trójkąta
 ?
?


Odpowiedź, że trójkąt III, była oczywista. Trochę mniej oczywiste było to, że
pozostałe trójkąty nie są przystające. Wtedy zadałem sobie pytanie: jak bez
twierdzenia Pitagorasa (a jeszcze go nie było!) przekonać moich uczniów, że
jakieś odcinki narysowane na papierze w kratkę są lub nie są równe? Weźmy
najprostszy przykład. Jak pokazać, że przeciwprostokątna trójkąta
prostokątnego o przyprostokątnych długości 3 i 4 ma długość 5? Inaczej
mówiąc, jak pokazać, że trójkąt
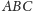 na rysunku obok jest
równoramienny? Okazało się to dość łatwe. Potrzebne były trzy rysunki
pomocnicze. Z lewej strony mamy pierwszy z nich. Jak pokazać, że punkty
na rysunku obok jest
równoramienny? Okazało się to dość łatwe. Potrzebne były trzy rysunki
pomocnicze. Z lewej strony mamy pierwszy z nich. Jak pokazać, że punkty
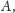
 i
i
 są współliniowe? Uczniowie szybko dostrzegli
przystające trójkąty
są współliniowe? Uczniowie szybko dostrzegli
przystające trójkąty
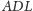 i
i
 (rys. z prawej strony). Zatem
kąty
(rys. z prawej strony). Zatem
kąty
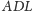 i
i
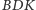 są równe, więc z twierdzenia o kątach
wierzchołkowych (nikt nie zawracał tu sobie głowy czymś takim, jak
twierdzenie odwrotne…) wynika, że punkty
są równe, więc z twierdzenia o kątach
wierzchołkowych (nikt nie zawracał tu sobie głowy czymś takim, jak
twierdzenie odwrotne…) wynika, że punkty

 i
i
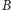 są
współliniowe. A więc punkty
są
współliniowe. A więc punkty
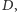
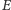 i
i
 na następnym
rysunku też są współliniowe. Potrzebny był jeszcze kąt
na następnym
rysunku też są współliniowe. Potrzebny był jeszcze kąt
 Narysowałem trzeci rysunek i zapytałem, jak dowieść, że kąt
Narysowałem trzeci rysunek i zapytałem, jak dowieść, że kąt
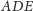 jest
prosty? Uczniowie zaproponowali kilka rozwiązań. Najprostsze z nich polegało
na zauważeniu, że trójkąty
jest
prosty? Uczniowie zaproponowali kilka rozwiązań. Najprostsze z nich polegało
na zauważeniu, że trójkąty
 i
i
 są przystające, zatem
„to, co z kąta prostego zabraliśmy kątem
są przystające, zatem
„to, co z kąta prostego zabraliśmy kątem
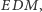 oddaliśmy z powrotem
kątem
oddaliśmy z powrotem
kątem
 ”. Mogliśmy teraz powrócić do pierwszego rysunku, na
którym dorysowaliśmy odcinek
”. Mogliśmy teraz powrócić do pierwszego rysunku, na
którym dorysowaliśmy odcinek
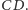 Uczniowie już natychmiast
dostrzegli, że trójkąty
Uczniowie już natychmiast
dostrzegli, że trójkąty
 i
i
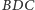 są przystające, więc
są przystające, więc
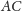 =
=
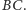
Niektórzy uczniowie byli nieco zdziwieni tym, że taki odcinek „ukośny” okazał się być równy „prostemu” (tzn. poziomemu). Trochę mnie zastanowiła pełna zdegustowania mina jednej uczennicy, zdająca się mówić: i po co to wszystko? Zrozumiałem po najbliższej klasówce, na której dałem zadanie podobne z trójkątem o przyprostokątnych 5 i 12. Rozwiązanie tej uczennicy było krótkie:

Te proste dowody geometryczne nie odwołujące się do twierdzenia Pitagorasa, skłoniły mnie do zastanowienia się nad geometrycznym rozwiązaniem równania Pitagorasa w liczbach całkowitych. Przedstawię teraz to rozwiązanie. Mamy więc równanie

i zakładamy, że
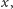
 i
i
 są całkowite. Łatwo pokazujemy,
że co najmniej jedna z liczb
są całkowite. Łatwo pokazujemy,
że co najmniej jedna z liczb
 i
i
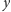 jest parzysta. Gdyby
bowiem
jest parzysta. Gdyby
bowiem

to

więc liczba
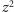 byłaby parzysta i niepodzielna przez 4, co jest niemożliwe.
Załóżmy zatem, że liczba
byłaby parzysta i niepodzielna przez 4, co jest niemożliwe.
Załóżmy zatem, że liczba
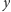 jest parzysta. Zauważmy, że wtedy liczby
jest parzysta. Zauważmy, że wtedy liczby
 i
i
 są tej samej parzystości. Narysujmy teraz trójkąt prostokątny
są tej samej parzystości. Narysujmy teraz trójkąt prostokątny
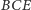 o bokach
o bokach
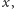
 i
i
 na papierze kratkowanym tak
jak na rysunku obok. Wierzchołki
na papierze kratkowanym tak
jak na rysunku obok. Wierzchołki
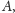
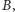
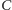 i
i
 leżą
w punktach kratowych, przy czym:
leżą
w punktach kratowych, przy czym:

Ponieważ liczby
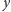 i
i
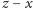 są parzyste, więc środek
są parzyste, więc środek
 odcinka
odcinka
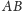 też leży w punkcie kratowym. Zastanówmy się teraz, jakie
punkty kratowe mogą leżeć na przeciwprostokątnej trójkąta prostokątnego
położonego w taki sposób, że przyprostokątne leżą na liniach tworzących
kratki.
też leży w punkcie kratowym. Zastanówmy się teraz, jakie
punkty kratowe mogą leżeć na przeciwprostokątnej trójkąta prostokątnego
położonego w taki sposób, że przyprostokątne leżą na liniach tworzących
kratki.
Lemat 1. Jeśli w trójkącie
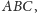 takim jak na rysunku obok,
takim jak na rysunku obok,
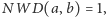 gdzie
gdzie
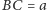 i
i
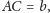 to jedynymi
punktami kratowymi leżącymi na przeciwprostokątnej
to jedynymi
punktami kratowymi leżącymi na przeciwprostokątnej
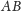 są jej
końce
są jej
końce
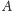 i
i
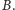
Dowód lematu wynika dość łatwo z twierdzenia Talesa, ale poradzimy sobie bez niego.
Dowód. Przypuśćmy, że
na przeciwprostokątnej leżą inne punkty kratowe i niech
 będzie
takim punktem leżącym najbliżej wierzchołka
będzie
takim punktem leżącym najbliżej wierzchołka
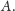 Niech
Niech
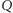 będzie rzutem punktu
będzie rzutem punktu
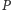 na bok
na bok
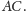 Niech
Niech
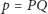 i
i
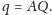 Odłóżmy następnie odcinek
Odłóżmy następnie odcinek
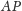 w odcinku
w odcinku
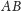 tyle razy, ile się da. Niech punkt
tyle razy, ile się da. Niech punkt
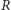 będzie
ostatnim z otrzymanych tak punktów przed wierzchołkiem
będzie
ostatnim z otrzymanych tak punktów przed wierzchołkiem
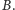 Niech wreszcie punkt
Niech wreszcie punkt
 będzie rzutem punktu
będzie rzutem punktu
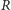 na bok
na bok
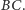 Podobnie jak na lekcji w gimnazjum pokazujemy, że wszystkie
punkty na przeciwprostokątnej, otrzymane w wyniku odkładania odcinka
Podobnie jak na lekcji w gimnazjum pokazujemy, że wszystkie
punkty na przeciwprostokątnej, otrzymane w wyniku odkładania odcinka
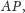 są kratowe. W szczególności punkty
są kratowe. W szczególności punkty
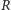 i
i
 są
kratowe. Przypuśćmy najpierw, że
są
kratowe. Przypuśćmy najpierw, że
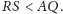 Weźmy taki punkt
Weźmy taki punkt
 na odcinku
na odcinku
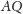 taki, że
taki, że
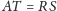 i weźmy punkt
i weźmy punkt
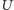 przeciwprostokątnej, że
przeciwprostokątnej, że
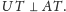 Oczywiście trójkąty
Oczywiście trójkąty
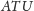 i
i
 są przystające, więc
są przystające, więc
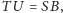 skąd wynika,
że punkt
skąd wynika,
że punkt
 jest punktem kratowym, co przeczy wyborowi punktu
jest punktem kratowym, co przeczy wyborowi punktu
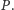 Zatem
Zatem
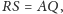 czyli odcinek
czyli odcinek
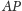 został odłożony
w odcinku
został odłożony
w odcinku
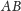 całkowitą liczbę razy, powiedzmy
całkowitą liczbę razy, powiedzmy
 razy.
Oczywiście
razy.
Oczywiście
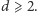 Wtedy
Wtedy
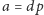 i
i
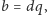 co przeczy
temu, że liczby
co przeczy
temu, że liczby
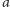 i
i
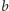 są względnie pierwsze.
są względnie pierwsze.
Wniosek. Jeśli
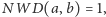 punkt
punkt
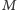 leży
na półprostej
leży
na półprostej
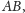
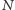 jest rzutem punktu
jest rzutem punktu
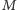 na prostą
na prostą
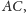
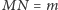 oraz
oraz
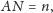 to istnieje liczba całkowita
to istnieje liczba całkowita
 taka, że
taka, że
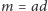 i
i
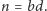
Lemat 2. Zachowajmy oznaczenia z lematu 1. Jeśli
 i
i
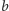 mają
wspólny dzielnik większy od 1, to na przeciwprostokątnej
mają
wspólny dzielnik większy od 1, to na przeciwprostokątnej
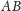 istnieją
inne punkty kratowe poza jej końcami.
istnieją
inne punkty kratowe poza jej końcami.
Dowód. Niech
 i
i
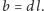 Narysujmy trójkąt prostokątny
Narysujmy trójkąt prostokątny
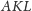 o przyprostokątnych
o przyprostokątnych
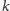 i
i
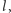 a następnie odłóżmy
a następnie odłóżmy
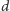 razy odcinek
razy odcinek
 w odcinku
w odcinku
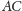 i
i
 razy odcinek
razy odcinek
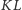 w odcinku
w odcinku
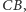 otrzymując punkty
otrzymując punkty

Niech następnie punkt kratowy
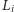 (dla
(dla
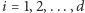 )
będzie punktem, którego rzutami na proste
)
będzie punktem, którego rzutami na proste
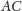 i
i
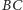 są
odpowiednio punkty
są
odpowiednio punkty
 oraz
oraz
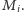 Pokazujemy, że punkty
Pokazujemy, że punkty

są współliniowe, a więc punkty
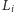 dla
dla
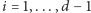 leżą
na przeciwprostokątnej
leżą
na przeciwprostokątnej
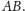
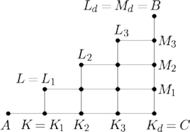
Powróćmy do naszego trójkąta prostokątnego o bokach długości

 i
i
 Niech
Niech
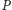 będzie punktem kratowym leżącym
na odcinku
będzie punktem kratowym leżącym
na odcinku
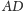 najbliżej punktu
najbliżej punktu
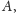 a
a
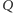 jego rzutem na
jego rzutem na
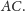
Niech następnie
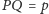 i
i
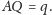 Z lematu 2 wynika, że
Z lematu 2 wynika, że
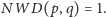 Z wniosku wynika, że istnieje liczba całkowita
Z wniosku wynika, że istnieje liczba całkowita
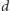 taka, że
taka, że

gdzie
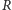 jest rzutem
jest rzutem
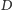 na
na
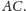 Odłóżmy następnie odcinek
Odłóżmy następnie odcinek
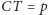 na półprostej
na półprostej
 i niech
i niech
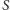 będzie takim punktem
półprostej
będzie takim punktem
półprostej
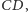 że
że
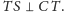 Ponieważ
Ponieważ
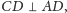 więc
kąty
więc
kąty
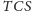 i
i
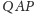 są równe, a zatem trójkąty
są równe, a zatem trójkąty
 i
i
 są przystające. Stąd wynika, że
są przystające. Stąd wynika, że
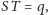 więc punkt
więc punkt
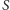 jest punktem kratowym. Z lematu 1 wynika, że istnieje liczba całkowita
jest punktem kratowym. Z lematu 1 wynika, że istnieje liczba całkowita
 taka, że
taka, że

Zatem

skąd wynika, że
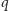 jest dzielnikiem
jest dzielnikiem
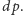 Ponieważ liczby
Ponieważ liczby
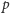 i
i
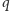 są względnie pierwsze, więc
są względnie pierwsze, więc
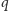 jest dzielnikiem
jest dzielnikiem
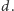 Istnieje więc liczba całkowita
Istnieje więc liczba całkowita
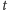 taka, że
taka, że
 Mamy
teraz
Mamy
teraz

czyli
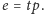 Zatem
Zatem

skąd ostatecznie dostajemy
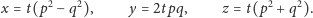 | (1) |
Dla każdego rozwiązania
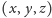 równania
równania

istnieją liczby całkowite
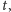
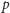 i
i
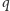 takie, że spełnione są
równości
takie, że spełnione są
równości
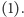 Z drugiej strony, łatwo sprawdzić, że jeśli
Z drugiej strony, łatwo sprawdzić, że jeśli
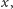
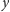 i
i
 są określone wzorami
są określone wzorami
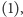 to spełniają równanie
Pitagorasa.
to spełniają równanie
Pitagorasa.