Jak pięknie. Niestety, mniej więcej 90 lat temu Bertrand Russell wpadł na pomysł, by rozważyć zbiór (nazwijmy go 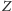), do którego ma należeć każdy taki zbiór, który nie jest sam swoim własnym elementem, i tylko takie zbiory. Inaczej mówiąc,

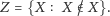
I oto okazało się, że coś jest nie tak jak trzeba. Mianowicie, czy 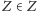? Jeśli tak, to 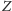nie może należeć 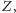do bo nie spełnia wymaganego warunku. Jeśli nie, to musi należeć do 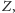bo spełnia wymagany warunek. Ta sprzeczność każe wnioskować, że taki zbiór 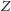nie może istnieć.

Mamy tu pierwszy przykład zbioru, który nie jest zbiorem, bo go nie ma. Przykład okazał się zresztą bardzo przydatny, bo matematycy zajęli się budową takich podstaw teorii mnogości, by podobne sprzeczności nie mogły wystąpić.

Swego czasu Georg Cantor udowodnił, że każdy zbiór ma mniej elementów niż podzbiorów. Mówiąc nieco dokładniej, jeśli w jakikolwiek sposób przyporządkujemy każdemu elementowi (dowolnego) zbioru 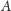pewien podzbiór zbioru 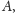to na pewno zostanie jeszcze sporo podzbiorów „bez przydziału”. (Mówiąc jeszcze dokładniej, moc zbioru 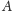jest ostro mniejsza od mocy zbioru 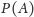wszystkich podzbiorów zbioru 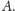) Z tego twierdzenia Cantora (spytajcie dowolnego studenta matematyki po I semestrze studiów, czy słyszał o twierdzeniu Cantora!) wynika kilka ciekawych wniosków pozytywnych, ale także wiele negatywnych, czyli takich, które mówią o tym, że coś nie istnieje.

Po pierwsze, nie istnieje „zbiór wszystkich zbiorów”, czyli taki zbiór, do którego należy każdy zbiór. Istotnie, przypuśćmy, że 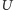jest takim zbiorem. Wtedy każdy jego podzbiór – będąc zbiorem – jest jednocześnie jego elementem, a zatem 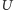ma nie więcej podzbiorów niż elementów – sprzeczność z twierdzeniem Cantora.

Widać mieliśmy za duże wymagania. Może uda się utworzyć zbiór wszystkich zbiorów jednoelementowych?

Takich jest przecież dużo mniej niż wszystkich zbiorów... Niestety. Gdyby taki zbiór, powiedzmy 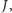istniał, to dla dowolnego zbioru 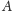elementem zbioru 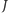byłby jednoelementowy zbiór 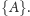Ale wtedy wzięlibyśmy sumę zbiorów należących do 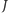(czyli zbiór złożony ze wszystkich takich elementów, które należą do choćby jednego elementu zbioru 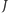) – a zgodnie z aksjomatami teorii mnogości, suma zbiorów należących do jednego zbioru jest znowu zbiorem – i okazałoby się, że elementem owej sumy jest każdy zbiór. Rzeczywiście, zbiór 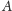jest elementem zbioru 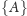należącego do 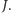A przecież już wiemy, że taki zbiór nie istnieje! Zatem nie istnieje także zbiór wszystkich zbiorów jednoelementowych.

A czy istnieje zbiór ze 149 podzbiorami? Znów pudło. Nie istnieje też zbiór, który miałby dokładnie 196 albo 245 280 podzbiorów. Uzasadnienie tej tezy nie wymaga sprawdzenia każdego zbioru i policzenia jego podzbiorów. Po prostu liczba podzbiorów skończonego zbioru -elementowego (oczywiście, żaden zbiór nieskończony nie ma dokładnie 149 podzbiorów!) jest równa 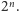Co więcej, ten fakt powinien być znany wielu uczniom szkoły średniej, a w każdym razie tym, którzy widzieli kiedyś następującą równość:

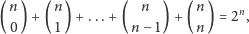
traktowaną jako własność kombinatoryczna. A przecież 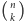to nic innego jak liczba
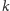-elementowych podzbiorów zbioru -elementowego! Zatem 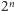 jest liczbą wszystkich (a więc i 0-elementowego i 1-elementowych, … i 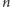-elementowego) podzbiorów zbioru 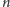-elementowego.

Dobrze, jeśli nie 149 i nie 196, i nie 245 280, to może da się znaleźć zbiór, który miałby tyle podzbiorów, ile jest liczb naturalnych (czyli przeliczalnie wiele)? Nie wątpię, że nie spodziewasz się już, drogi Czytelniku, odpowiedzi pozytywnych w tym artykule. I rzeczywiście. Żaden zbiór skończony nie ma tylu podzbiorów, bo ma ich tylko skończenie wiele. Jeśli natomiast 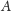jest zbiorem nieskończonym, to ma co najmniej tyle elementów, ile jest liczb naturalnych, bo po wyjęciu 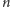 elementów z 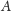– dla dowolnej liczby naturalnej – możemy jeszcze znaleźć w nim kolejny, 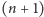-szy element. 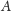Jeśli tak, to z twierdzenia Cantora wynika, że musi mieć więcej podzbiorów niż jest liczb naturalnych!

Po tym wszystkim można zapytać, czy w ogóle istnieją jakieś zbiory. Tak. Na pewno istnieje zbiór pusty.