A jednak się da!

O łganiu w żywe oczy

W poprzednim odcinku naszej sagi przedstawiliśmy miłosną historię Aldony i Bogumiła. Poniżej prezentujemy jej dość dramatyczną kontynuację, widzianą oczami Aldony...

Problem. Aldona ma problem sercowy. Na dyskotece z okazji ostatniego dnia kolonii poznała chłopaka, Bogumiła. Był całkiem sympatyczny, więc nawet ucieszyła się, gdy zadzwonił do niej kilka dni po zakończeniu wyjazdu. Umówili się na ciastka, przyniósł jej bardzo ładne kwiatki i tak zaczęli się spotykać. Bogumił wydaje się bardzo porządny, jednak jakaś część serca Aldony wciąż tęsknie wzdycha do innego poznanego na koloniach chłopaka, Dobromira, z którym od pewnego czasu koresponduje. Aldona nie jest jeszcze pewna swoich uczuć i nie chciałaby zamykać się na żadną z możliwości, co jest zupełnie zrozumiałe. Problem w tym, że Bogumił zdaje się wiedzieć o jej kontakcie z Dobromirem i być może lada chwila będzie się od niej domagał ujawnienia korespondencji. Aldona jest wielką miłośniczką kryptografii, w związku z czym do komunikacji z Dobromirem używa protokołu szyfrowania RSA. Niestety, Bogumił nie jest w ciemię bity i wie, że w tym protokole Aldona nie może udawać, że zaszyfrowała inną wiadomość niż w rzeczywistości. Czy istnieje sposób, dzięki któremu Aldona mogłaby wmawiać Bogumiłowi, że przesyłane przez nią do Dobromira listy mają treść inną niż naprawdę?

Protokół, którego potrzebuje Aldona, nosi nazwę szyfrowania wypieralnego (jest to dość karkołomna próba autora tłumaczenia angielskiego terminu deniable encryption). Zanim mu się przyjrzymy, wyjaśnijmy najpierw, na czym polega wspomniana w powyższej historii wada szyfrowania RSA. Temu szyfrowaniu poświęcony był pierwszy odcinek sagi, zamieszczony w 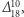$10 ∆ 18,$ poniżej przedstawiamy skrótowe przypomnienie:

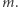Zauważmy, że oszalały z zazdrości Bogumił, który nakrył Aldonę na wysyłaniu szyfrogramu (czyli zaszyfrowanej wiadomości) $c$ do Dobromira, mógłby próbować wymusić na niej ujawnienie treści wiadomości $m.$ Niestety, Aldona nie mogłaby udać, że chciała wysłać inną wiadomość 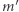$m ′$ niż w rzeczywistości. 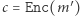Bogumił ma dostęp do klucza publicznego $e$ i wie, na czym polega szyfrowanie, w związku z czym wystarczy, że sprawdzi, czy $c = Enc(m ′)$ - jeśli nie, dowiaduje się, że 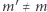$|m′ ≠m$ i Aldona próbowała go oszukać, co czyni go jeszcze bardziej sfrustrowanym. Można odnieść wrażenie, że nie sposób skonstruować protokołu szyfrowania z kluczem publicznym, który byłby pozbawiony tego mankamentu - rzecz jasna, gdyby to była prawda, nie pisalibyśmy o tym w ramach naszego cyklu: A jednak się da!

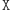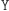Naturalnie, wystarczy nam umiejętność wypieralnego szyfrowania pojedynczego bitu - wszak dowolnie długą wiadomość można rozbić na bity i osobno zaszyfrować każdy z nich. 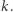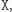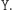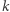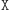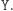Takie szyfrowanie można przedstawić w postaci dwóch czynności: $X$ i $|Y$ oraz klucza $k.$ Dobromir informuje Aldonę, że jeśli chce ona wysłać do niego bit 0, powinna wykonać czynność $X,$ a jeśli chce wysłać 1 - wykonuje $|Y.$ Klucz $|k$ powinien pozwalać Dobromirowi na rozstrzygnięcie, czy Aldona wykonała $|X$ czy $|Y.$ Oczywiście, aby to szyfrowanie miało sens, bez znajomości 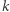$|k$ to rozstrzygnięcie powinno być bardzo trudne. Rozważane szyfrowanie będzie wypieralne, jeśli dla żadnej z tych czynności nie istnieje dowód (niewymagający klucza 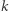$k$ ), że wykonało się właśnie tę czynność. Istotnie, gdyby dla którejś z nich istniał taki dowód (powiedzmy dla 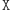$|X$ ), to po wykonaniu 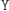$Y$ Aldona nie mogłaby udawać przed Bogumiłem, że uczyniła 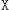$|X$ (gdyż wówczas Bogumił wie, że może domagać się dowodu, a jeśli go nie dostanie, dowiaduje się, że Aldona ma przed nim jakieś sekrety).

Najpierw przedstawimy protokół, w którym tylko czynność 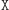$X$ będzie pozbawiona wspomnianego "dowodu wykonania" (czyli Aldona może udawać, że przesłała 0, gdy przesłała 1, ale nie odwrotnie). W tym wypadku 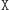$|X$ będzie oznaczać przesłanie Dobromirowi losowego elementu ze zbioru 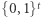$|{0,1}t$ (tzn. zbioru ciągów binarnych długości 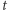$t$ ) dla pewnej (dużej) liczby naturalnej 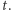$t.$ Czynnością 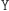$|Y$ będzie z kolei wysłanie losowego elementu z pewnego podzbioru 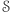$𝒮$ zbioru 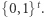${0, 1}t.$ Pojawia się tutaj pewien szkopuł - przecież element z 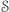$|𝒮$ jest również elementem z 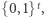$t |{0,1},$ zatem po wykonaniu 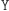$Y$ Dobromir nie jest w stanie stwierdzić ze stuprocentową pewnością, że nie zostało wykonane 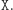$X.$ Sto procent to faktycznie za dużo, ale jeśli zbiór 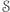$𝒮$ jest dostatecznie mały w stosunku do 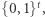$|{0,1}t,$ to szansa na wybór elementu z 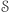$𝒮$ przy losowaniu z 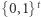$t {0,1}$ jest pomijalnie mała (mniejsza niż, powiedzmy, 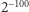$2−100$ ), w związku z tym czynności 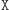$X$ i $|Y$ 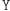mają praktycznie rozłączne skutki. Pojawiło się nam w ten sposób pierwsze naturalne wymaganie wobec zbioru $𝒮$ :

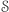(a): stosunek 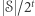$| 𝒮 /2t$ jest bardzo mały.

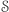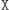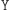Kolejne wymagania wobec zbioru $|𝒮$ są bezpośrednimi konsekwencjami sformułowanych wcześniej własności czynności $X$ i $|Y$ prowadzących do uzyskania protokołu szyfrowania ( "połowicznie") wypieralnego:

(b): łatwo generować losowe elementy zbioru 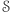$|𝒮$ bez znajomości klucza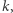 $k,$
(c): bez znajomości klucza 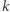$|k$ trudno stwierdzić, czy dany 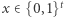$x ∈ {0,1}t$ należy do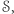 $𝒮,$
(d): znając klucz 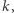$k,$ łatwo stwierdzić, czy dany 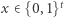$x ∈ {0,1}t$ należy do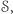 $𝒮,$
(e): bez znajomości klucza 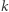$|k$ praktycznie nie sposób udowodnić, że dany 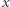$x$ nienależący do 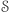$𝒮$ faktycznie nie należy do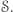 $𝒮.$

Uff, pozostaje nam teraz "tylko" wskazać taki magiczny (można poetycko napisać: przezroczysty) zbiór 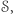$|𝒮,$ spełniający własności (a)-(e). Zwrócimy najpierw uwagę na pewną charakterystyczną własność funkcji 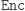$|Enc$ przy szyfrowaniu z kluczem publicznym. Jej obliczenie jest proste, natomiast jej odwrócenie bardzo trudne, o ile nie znamy klucza prywatnego. 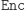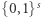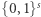Jeśli potraktować $|Enc$ jako funkcję z ${0,1}s$ do $s |{0,1}$ dla pewnej liczby naturalnej $s$ (możemy tak zrobić, zapisując argumenty i wartości w postaci binarnej), takie funkcje zwykło się nazywać funkcjami jednokierunkowymi z zapadką - łatwo obliczać ich wartości i trudno je odwracać (jednokierunkowość) bez podpowiedzi (zapadki).

Okazuje się, że dla każdej funkcji jednokierunkowej 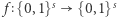$f {0,1}s {0, 1}s$ można wskazać "funkcję trudnego bitu", tzn. funkcję 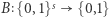$s |B {0,1} {0,1}$ taką, że 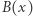$|B(x)$ jest trudne do obliczenia, jeśli znamy tylko wartość 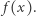$f (x).$ Mówi o tym twierdzenie Goldreicha-Levina. Odpowiednie definicje "trudności" są w tym kontekście dość skomplikowane - na potrzeby artykułu ograniczymy się do stwierdzenia, że dla odpowiednio dużych wartości $|s$ z omawianymi tutaj trudnymi zadaniami nie poradzi sobie żaden ziemski komputer.

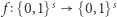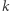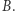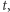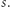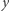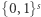Ustalmy pewną funkcję jednokierunkową $f {0,1}s {0,1}s$ z zapadką $|k$ oraz odpowiadającą jej funkcję trudnego bitu $B.$ Ustalmy liczbę naturalną $|t,$ (dużo) większą od $|s.$ Dla dowolnego ciągu $|y$ z $s {0,1}$ rozważmy ciąg z 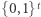$t |{0,1}$ powstały przez dołączenie do 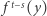$| ft− s(y)$ (gdzie "potęgowanie" funkcji oznacza krotność iteracji) "trudnych bitów" z 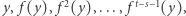$y, f (y), f2(y),..., ft−s− 1(y),$ a zbiór tak powstałych ciągów oznaczmy przez 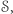$|𝒮,$ to znaczy

𝒮 = { ft−s(y) B(y) B( f(y)) B( f 2(y)) ... B(f t−s− 1(y)) y ∈{0,1}s},

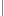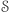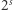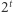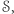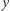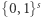gdzie znak " $\text{[math]}$ " oznacza łączenie ciągów. Zbiór $𝒮$ ma wszystkie pożądane własności! Istotnie, jego rozmiar to $2s$ (co w porównaniu z $t |2$ jest bardzo małe, więc spełnione jest (a)), a sposób generowania elementów z $𝒮,$ wychodzący od dowolnego elementu $|y$ z $|{0,1}s$ (i niewymagający klucza 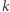$k$ ), został przedstawiony wyżej (własność (b)). Jeśli dostaniemy dowolny 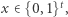$|x∈ {0,1}t,$ to aby stwierdzić, czy jest to element z 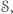$|𝒮,$ musielibyśmy sprawdzić, czy jego ostatnie 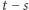$t− s$ bity są "trudnymi bitami" dla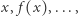 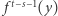$x, f (x),...,$ $f t− s−1(y)$ dla pewnego 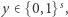$y ∈{0,1}s,$ o którym wiemy jedynie, ile wynosi 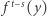$| ft− s(y)$ (jest to pierwsze $s$ bitów $x$ ). 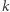Zgodnie z definicją "trudnego bitu", bez znajomości $k$ jest to zadanie trudne (zatem spełniona jest własność (c)), a znając 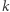$|k$ - łatwe (co oznacza (d)). 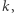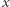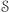Ponadto, nie znając $k,$ praktycznie nie można udowodnić, że dany $|x$ spoza $𝒮$ faktycznie do niego nie należy - ponownie, jak poprzednio, należałoby obliczyć odpowiednie "trudne bity" i uzasadnić, że się nie zgadzają z "ogonem" 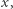$x,$ a tego bez klucza zrobić nie umiemy, co uzasadnia ostatnią własność (e). Przypomnijmy jednak, że nasz sukces jest niestety połowiczny - Aldona może udawać tylko "w jedną stronę".

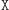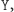Teraz czas na przedstawienie czynności $X$ i $|Y,$ z których obie są pozbawione "dowodu wykonania" (no dobrze - tak szczerze mówiąc, jedna z nich będzie go pozbawiona z dużym prawdopodobieństwem). Polega on na odpowiednim "zamaskowaniu" kłopotliwej sytuacji, której doświadczyliśmy poprzednio. Teraz Aldona wybiera liczbę naturalną 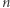$|n$ i losuje 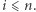$i⩽ n.$ Następnie losuje 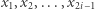$|x1,x2,...,x2i−1$ ze zbioru 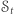$|𝒮t$ oraz (jeśli 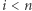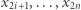$|i < n$ ) $|x2i+1,...,x2n$ ze zbioru 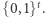$|{0,1}t.$ Czynność 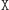$|X$ polega na wylosowaniu 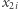$x 2i$ ze zbioru 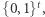${0,1}t,$ a czynność 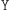$Y$ - na wylosowaniu 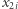$|x2i$ ze zbioru 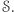$𝒮.$ Oczywiście Dobromir - podobnie jak poprzednio - może bez problemu sprawdzić, co chciała przesłać Aldona. Ponadto, jeśli Aldona zrobiła 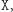$X,$ może śmiało wmawiać Bogumiłowi, że zrobiła 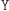$Y$ - wystarczy, że będzie twierdzić, że 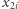$|x 2i$ było wylosowane z 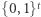$t |{0,1}$ (czego i tak nie byłaby w stanie udowodnić), oraz pokaże mu, jak wygenerowała 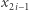$|x2i−1$ (co będzie dowodem, że należy ono do 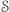$|𝒮$ ). 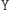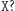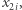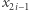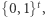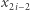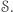Co, jeśli Aldona zrobiła $Y$ i chce przekonać Bogumiła, że było to $|X?$ Wtedy może mu powiedzieć, że zarówno $x , 2i$ jak i $x 2i− 1$ były wylosowane z $t {0, 1} ,$ i pokaże, jak wygenerowała $x2i−2$ z $𝒮.$ W takim przypadku Bogumił również nie jest w stanie wykryć szwindlu. Czy aby na pewno? Zauważmy, że Aldona może nieszczęśliwie wylosować 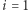$|i = 1$ i wówczas, jeśli zrobiła 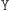$Y$ i chce wmówić Bogumiłowi, że było inaczej, to twierdziłaby, że wszystkie liczby 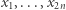$x1,...,x2n$ były wylosowane z 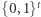$|{0,1}t$ - taka sytuacja nie jest jednak dopuszczalna przez protokół. Wydawać by się mogło, że nie jest to problem - przecież to Aldona jest "stroną losującą", więc jeśli wylosuje 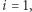$i = 1,$ może śmiało powtórzyć losowanie. Dla jednego bitu takie oszustwo mogłoby przejść, ale (jak to w kryptografii) zakładamy, że przeciwnik (tutaj, niestety, Bogumił) "zna system" i w końcu zorientowałby się, że protokół nie jest taki, jak mówimy (tzn. nigdy nie wylosowaliśmy 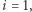$i = 1,$ chociaż po dłuższym czasie powinno to się zdarzyć). W tej sytuacji należy po prostu uznać, że nasze rozwiązanie nie jest idealne i z grubsza "raz na 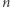$n$ ", niestety, próba oszustwa wychodzi na jaw.

Rzecz jasna, opisane tu uczuciowe rozterki miały jedynie dodać całej historii kolorytu. Mamy jednak nadzieję, że Czytelnikom łatwo będzie uwierzyć w znaczenie przedstawionej idei dla bezpieczeństwa w cyberprzestrzeni.