Drobiazgi
Od Pascala do Pitagorasa i dalej
Twierdzenie Pascala o równomiernym ciśnieniu gazu na ścianki naczynia pociąga za sobą twierdzenie Pitagorasa i jego uogólnienie, czyli twierdzenie kosinusów.
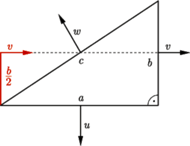
Rys. 1
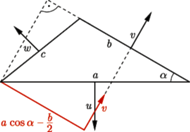
Rys. 2
Wyobraźmy sobie pudełko w kształcie trójkąta prostokątnego i o głębokości 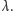 Pudełko to jest położone poziomo i przymocowane w jednym z wierzchołków doskonałym łożyskiem do pionowej osi. Pudełko wypełniamy gazem, który prze na każdą ściankę. Parcie na górną i dolną jest jednakowe, więc one się znoszą. Jednak znosić się muszą i parcia na ścianki boczne. Przyjrzyjmy się im. Zgodnie z prawem Pascala mamy (Rys. 1)
Pudełko to jest położone poziomo i przymocowane w jednym z wierzchołków doskonałym łożyskiem do pionowej osi. Pudełko wypełniamy gazem, który prze na każdą ściankę. Parcie na górną i dolną jest jednakowe, więc one się znoszą. Jednak znosić się muszą i parcia na ścianki boczne. Przyjrzyjmy się im. Zgodnie z prawem Pascala mamy (Rys. 1)

Równość momentów tych sił to

czyli 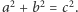
Dla trójkąta nieprostokątnego otrzymujemy (Rys. 2)

czyli 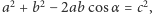 a więc twierdzenie kosinusów.
a więc twierdzenie kosinusów.
Na tym przykładzie widać przewagę fizyki nad matematyką, bo z twierdzenia Pitagorasa, a nawet kosinusów, twierdzenia Pascala wyprowadzić się raczej nie da.