Klub 44M - zadania III 2016»Zadanie 718
o zadaniu...
- Zadanie pochodzi z artykułu Klub 44M - zadania III 2016
- Publikacja w Delcie: marzec 2016
- Publikacja elektroniczna: 29 lutego 2016
- Artykuł źródłowy w wersji do druku [application/pdf]: (84 KB)
-
Zadanie 718 zaproponował pan Tomasz Ordowski.
Dowieść, że dla dowolnych dodatnich liczb całkowitych 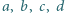 zachodzi równość
zachodzi równość
![[a, b,c,d] =-a⋅b-⋅c⋅d- ⋅--(a,-b,c)⋅(a,b,d)-⋅(a,c,d)-⋅(b,c,d)---. (a, b,c,d) (a,b) ⋅(a,c)⋅(a,d) ⋅(b,c) ⋅(b,d) ⋅(c,d)](/math/temat/matematyka/teoria_liczb/zadania/2016/02/29/zm-k44-718/2x-f64cd4667e200cae0b647d7a1c3170835ae3432d-dm-2C,6B,73-FF,FF,FF.gif)
Nawias kwadratowy oznacza najmniejszą wspólną wielokrotność, zaś nawias okrągły - największy wspólny dzielnik liczb ujętych w ów nawias.
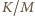 (licznik
(licznik 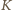 to iloczyn ośmiu czynników, mianownik
to iloczyn ośmiu czynników, mianownik 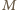 to iloczyn siedmiu czynników). Lewa strona to
to iloczyn siedmiu czynników). Lewa strona to ![|L = [a,b,c,d].](/math/temat/matematyka/teoria_liczb/zadania/2016/02/29/zm-k44-718/4x-3ae01d082f06ba518fa4af60a10f4ff5720e5299-im-66,57,43-FF,FF,FF.gif) Wystarczy pokazać, że dowolna liczba pierwsza wchodzi do rozkładów liczb
Wystarczy pokazać, że dowolna liczba pierwsza wchodzi do rozkładów liczb 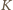 oraz
oraz 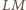 w jednakowej potędze (być może zerowej).
w jednakowej potędze (być może zerowej).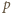 i przyjmijmy, że liczby
i przyjmijmy, że liczby  są podzielne odpowiednio przez
są podzielne odpowiednio przez 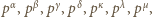 ale nie przez
ale nie przez 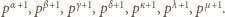 Wówczas
Wówczas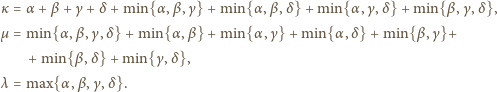

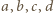 ) nie tracimy ogólności zakładając, że
) nie tracimy ogólności zakładając, że  Napisane równości uzyskują postać
Napisane równości uzyskują postać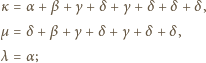
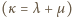 gotowa.
gotowa. Wykazać, że zbiór wszystkich liczb całkowitych nieujemnych może być przedstawiony jako suma rozłącznych zbiorów trójelementowych, przy czym w każdym z tych zbiorów liczba środkowa (co do wielkości) różni się od jednej z dwóch pozostałych liczb o
Wykazać, że zbiór wszystkich liczb całkowitych nieujemnych może być przedstawiony jako suma rozłącznych zbiorów trójelementowych, przy czym w każdym z tych zbiorów liczba środkowa (co do wielkości) różni się od jednej z dwóch pozostałych liczb o 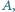 zaś od drugiej o
zaś od drugiej o 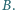
 Wskażemy indukcyjną konstrukcję ciągu zbiorów
Wskażemy indukcyjną konstrukcję ciągu zbiorów 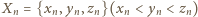 o wymaganych własnościach. Zaczniemy od trójki
o wymaganych własnościach. Zaczniemy od trójki  Załóżmy, że zbiory
Załóżmy, że zbiory 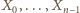 zostały już określone. Wówczas definiujemy
zostały już określone. Wówczas definiujemy  jako najmniejszą liczbę naturalną jeszcze niewykorzystaną (tzn. nieobecną w zbiorze
jako najmniejszą liczbę naturalną jeszcze niewykorzystaną (tzn. nieobecną w zbiorze 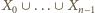 ) - to już gwarantuje, że w wyniku całej konstrukcji wszystkie liczby naturalne zostaną użyte oraz że ciąg
) - to już gwarantuje, że w wyniku całej konstrukcji wszystkie liczby naturalne zostaną użyte oraz że ciąg 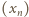 będzie rosnący.
będzie rosnący.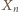 (gdy
(gdy  już mamy), patrzymy na liczbę
już mamy), patrzymy na liczbę 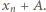 Jeżeli jest ona jeszcze niewykorzystana, przyjmujemy ją jako
Jeżeli jest ona jeszcze niewykorzystana, przyjmujemy ją jako 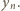 Jeżeli jest wykorzystana, bierzemy jako
Jeżeli jest wykorzystana, bierzemy jako  liczbę
liczbę 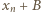 ; i z konieczności przyjmujemy
; i z konieczności przyjmujemy  (tak więc jedna z różnic
(tak więc jedna z różnic 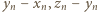 będzie równa
będzie równa  a druga
a druga 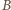 ). Tak określona liczba
). Tak określona liczba 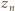 jest większa od liczb
jest większa od liczb 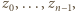 więc nie została wcześniej wykorzystana.
więc nie została wcześniej wykorzystana.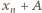 została już wykorzystana, wówczas liczba
została już wykorzystana, wówczas liczba 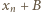 pozostała niewykorzystana (i może być użyta jako
pozostała niewykorzystana (i może być użyta jako  ). Przypuśćmy, że liczba
). Przypuśćmy, że liczba  znalazła się w którymś zbiorze
znalazła się w którymś zbiorze  o numerze
o numerze 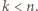 Skoro
Skoro 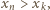 to
to 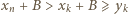 ; musiałaby zajść równość
; musiałaby zajść równość 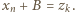 Ale
Ale  więc mielibyśmy
więc mielibyśmy 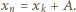 Liczba
Liczba 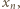 niewykorzystana aż do
niewykorzystana aż do 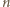 -tego kroku konstrukcji, tym bardziej nie była jeszcze wykorzystana w momencie konstrukcji zbioru
-tego kroku konstrukcji, tym bardziej nie była jeszcze wykorzystana w momencie konstrukcji zbioru 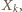 więc na mocy przyjętego algorytmu powinna była zostać użyta jako
więc na mocy przyjętego algorytmu powinna była zostać użyta jako 
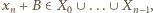 i uzasadnia poprawność określenia
i uzasadnia poprawność określenia 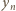 ; powstały zbiór
; powstały zbiór 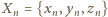 jest rozłączny ze zbiorami
jest rozłączny ze zbiorami 
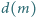 oznacza liczbę dodatnich dzielników liczby naturalnej
oznacza liczbę dodatnich dzielników liczby naturalnej 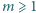
 spełniających równanie
spełniających równanie 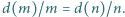
 spełniających równanie
spełniających równanie 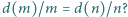
 gdzie
gdzie 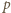 jest nieparzystą liczbą pierwszą, ma wymaganą własność, bowiem
jest nieparzystą liczbą pierwszą, ma wymaganą własność, bowiem 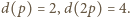
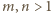 spełnia podane równanie:
spełnia podane równanie: 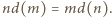 Skoro liczby
Skoro liczby  są względnie pierwsze, wynika stąd, że
są względnie pierwsze, wynika stąd, że  jest dzielnikiem liczby
jest dzielnikiem liczby 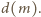 Wobec tego
Wobec tego 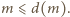 Taka nierówność zajść może (w formie równości) tylko wtedy, gdy każda liczba ze zbioru
Taka nierówność zajść może (w formie równości) tylko wtedy, gdy każda liczba ze zbioru 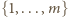 jest dzielnikiem liczby
jest dzielnikiem liczby  W szczególności
W szczególności  musi dzielić się przez
musi dzielić się przez 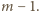 To zaś ma miejsce jedynie dla
To zaś ma miejsce jedynie dla 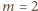 (rozważamy, z założenia, tylko
(rozważamy, z założenia, tylko 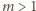 ).
).
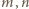 są symetryczne; to samo rozumowanie pokazuje, że także
są symetryczne; to samo rozumowanie pokazuje, że także 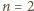 ; sprzeczność z założeniem, że
; sprzeczność z założeniem, że 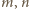 są względnie pierwsze. Nie istnieje więc para, o jakiej mowa w pytaniu (b).
są względnie pierwsze. Nie istnieje więc para, o jakiej mowa w pytaniu (b).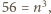 to
to 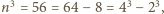 czyli
czyli 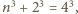 sprzecznie z Wielkim Twierdzeniem Fermata.
sprzecznie z Wielkim Twierdzeniem Fermata. które tworzą ciąg arytmetyczny.
które tworzą ciąg arytmetyczny. o wyrazach całkowitych dodatnich, w którym każda dodatnia liczba całkowita występuje jednokrotnie, przy czym dla każdego
o wyrazach całkowitych dodatnich, w którym każda dodatnia liczba całkowita występuje jednokrotnie, przy czym dla każdego  suma
suma 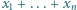 jest podzielna przez
jest podzielna przez 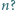
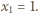 Będziemy przedłużać zdefiniowany odcinek ciągu, dołączając po dwa wyrazy.
Będziemy przedłużać zdefiniowany odcinek ciągu, dołączając po dwa wyrazy. i przyjmijmy, że wyrazy
i przyjmijmy, że wyrazy 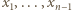 są już określone. Najmniejsza dodatnia liczba całkowita, różna od
są już określone. Najmniejsza dodatnia liczba całkowita, różna od 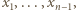 będzie wyrazem
będzie wyrazem  (to gwarantuje, że w budowanym ciągu znajdą się wszystkie liczby całkowite dodatnie).
(to gwarantuje, że w budowanym ciągu znajdą się wszystkie liczby całkowite dodatnie).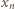 wzorem
wzorem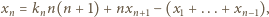
 jest liczbą całkowitą tak dobraną, by uzyskana liczba
jest liczbą całkowitą tak dobraną, by uzyskana liczba 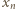 była dodatnia oraz różna od liczb
była dodatnia oraz różna od liczb 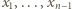 i różna od
i różna od 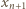 (powstający ciąg będzie więc miał wszystkie wyrazy różne). Przy tym
(powstający ciąg będzie więc miał wszystkie wyrazy różne). Przy tym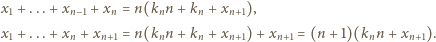
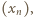 jakiego szukamy.
jakiego szukamy.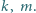 Niech
Niech 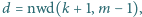
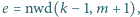
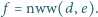 Dowieść, że liczba
Dowieść, że liczba 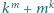 dzieli się przez
dzieli się przez 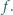
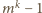 dzieli się przez
dzieli się przez 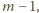 więc i przez
więc i przez 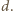 Wobec nieparzystości
Wobec nieparzystości 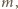 liczba
liczba 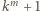 dzieli się przez
dzieli się przez 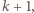 więc i przez
więc i przez 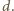 Zatem suma tych dwóch liczb, czyli
Zatem suma tych dwóch liczb, czyli  dzieli się przez
dzieli się przez 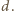 Z symetrii warunków zadania wynika, że
Z symetrii warunków zadania wynika, że 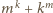 dzieli się także przez
dzieli się także przez 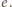 W takim razie dzieli się przez liczbę
W takim razie dzieli się przez liczbę 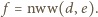
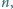 dla których liczba
dla których liczba
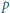 i
i 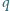 mają tę własność, że liczba
mają tę własność, że liczba 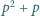 jest podzielna przez
jest podzielna przez 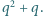 Udowodnij, że liczba
Udowodnij, że liczba 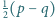 jest złożona.
jest złożona.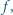 odwzorowująca zbiór liczb całkowitych dodatnich w siebie, jest niemalejąca i spełnia równość
odwzorowująca zbiór liczb całkowitych dodatnich w siebie, jest niemalejąca i spełnia równość 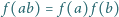 dla dowolnych liczb względnie pierwszych
dla dowolnych liczb względnie pierwszych 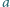 i
i 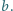 Udowodnić, że
Udowodnić, że
 wynika prawdziwość dwóch nierówności:
wynika prawdziwość dwóch nierówności: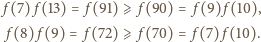
 ] wykazał, że funkcja
] wykazał, że funkcja 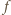 spełniająca podane warunki musi być postaci
spełniająca podane warunki musi być postaci 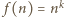 dla pewnego
dla pewnego 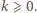
 będzie ustaloną dodatnią liczbą nieparzystą. Wyznaczyć największą możliwą liczność zbioru złożonego z liczb całkowitych dodatnich, mniejszych od
będzie ustaloną dodatnią liczbą nieparzystą. Wyznaczyć największą możliwą liczność zbioru złożonego z liczb całkowitych dodatnich, mniejszych od 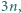 w którym każde dwa różne elementy mają i różnicę, i sumę różną od
w którym każde dwa różne elementy mają i różnicę, i sumę różną od 
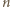 jest nieparzysta, zatem zbiór wszystkich liczb parzystych, mniejszych od
jest nieparzysta, zatem zbiór wszystkich liczb parzystych, mniejszych od 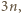 ma własność, o którą chodzi. Jest ich
ma własność, o którą chodzi. Jest ich  Wykażemy, że jest to największa możliwa liczność.
Wykażemy, że jest to największa możliwa liczność. na rozłączne pary:
na rozłączne pary: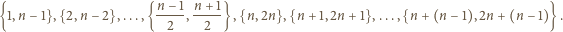
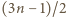 par liczb. Zbiór o większej liczności (zawarty w
par liczb. Zbiór o większej liczności (zawarty w 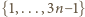 ) musi zawierać jedną z wymienionych par. Ale w każdej parze albo suma, albo różnica elementów jest równa
) musi zawierać jedną z wymienionych par. Ale w każdej parze albo suma, albo różnica elementów jest równa 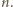 Stąd nasza teza.
Stąd nasza teza.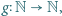 spełniającej warunek
spełniającej warunek 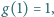 istnieje funkcja
istnieje funkcja 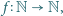 spełniająca warunki
spełniająca warunki 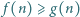 dla
dla 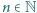 oraz
oraz 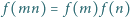 dla każdej pary liczb względnie pierwszych
dla każdej pary liczb względnie pierwszych 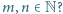 (
(  to zbiór wszystkich liczb całkowitych dodatnich).
to zbiór wszystkich liczb całkowitych dodatnich).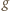 łatwo wskazać funkcję
łatwo wskazać funkcję  o wymaganych własnościach. Niech
o wymaganych własnościach. Niech 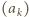 będzie rosnącym ciągiem wszystkich potęg liczb pierwszych:
będzie rosnącym ciągiem wszystkich potęg liczb pierwszych: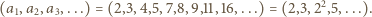
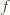 (o własności
(o własności 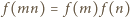 gdy
gdy  ) jest wyznaczona przez ciąg wartości
) jest wyznaczona przez ciąg wartości 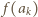 ; zaś podany warunek multyplikatywności nie stawia na owe wartości żadnych ograniczeń. Wobec tego konstruujemy taki ciąg indukcyjnie. Niech
; zaś podany warunek multyplikatywności nie stawia na owe wartości żadnych ograniczeń. Wobec tego konstruujemy taki ciąg indukcyjnie. Niech  będzie dowolną liczbą naturalną większą od
będzie dowolną liczbą naturalną większą od 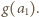
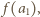 …,
…, 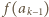 zostały już określone. Patrzymy na zbiór wszystkich liczb postaci
zostały już określone. Patrzymy na zbiór wszystkich liczb postaci 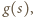 gdzie
gdzie  jest iloczynem różnych liczb ze zbioru
jest iloczynem różnych liczb ze zbioru 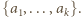 Określamy
Określamy 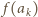 jako dowolną liczbę naturalną większą od wszystkich takich liczb
jako dowolną liczbę naturalną większą od wszystkich takich liczb 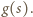
 wraz z warunkiem multyplikatywności, jednoznacznie generuje funkcję
wraz z warunkiem multyplikatywności, jednoznacznie generuje funkcję 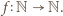 Spełnia ona także pozostały z zadanych warunków; jeśli bowiem liczba
Spełnia ona także pozostały z zadanych warunków; jeśli bowiem liczba 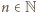 zostanie zapisana jako iloczyn
zostanie zapisana jako iloczyn 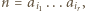 gdzie
gdzie 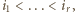 wówczas
wówczas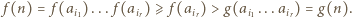
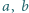 i
i  różne od zera, że liczba
różne od zera, że liczba 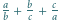 jest całkowita. Wykazać, że iloczyn
jest całkowita. Wykazać, że iloczyn  jest sześcianem liczby całkowitej.
jest sześcianem liczby całkowitej.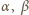 i
i 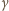 są niepodzielne przez liczbę pierwszą
są niepodzielne przez liczbę pierwszą 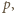 oraz że dla pewnej trójki liczb całkowitych nieujemnych
oraz że dla pewnej trójki liczb całkowitych nieujemnych 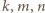 zachodzą równości
zachodzą równości 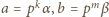 i
i 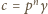 (w dalszym ciągu myślę, że zadanie nie jest trudne). Aby wykazać, że iloczyn
(w dalszym ciągu myślę, że zadanie nie jest trudne). Aby wykazać, że iloczyn 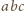 jest sześcianem pewnej liczby całkowitej, wystarczy przecież wykazać, iż każdy czynnik pierwszy występuje w rozkładzie tej liczby z wykładnikiem podzielnym przez
jest sześcianem pewnej liczby całkowitej, wystarczy przecież wykazać, iż każdy czynnik pierwszy występuje w rozkładzie tej liczby z wykładnikiem podzielnym przez 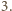 Mamy
Mamy 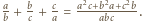 Mianownik tego ułamka jest podzielny przez liczbę
Mianownik tego ułamka jest podzielny przez liczbę 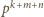 i niepodzielny przez
i niepodzielny przez 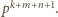 Zastąpienie uporządkowanej trójki liczb
Zastąpienie uporządkowanej trójki liczb 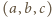 trójką
trójką 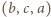 lub
lub 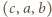 powoduje, że liczba
powoduje, że liczba 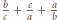 lub
lub 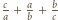 - więc ta z treści zadania - ma być całkowita (trójka
- więc ta z treści zadania - ma być całkowita (trójka 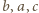 to jednak coś innego, bo na ogół
to jednak coś innego, bo na ogół 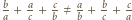 ). Można więc założyć, że
). Można więc założyć, że 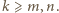 Mamy
Mamy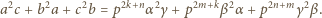
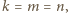 to
to 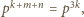 więc
więc 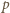 występuje w rozkładzie iloczynu
występuje w rozkładzie iloczynu 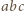 na czynniki pierwsze z wykładnikiem
na czynniki pierwsze z wykładnikiem 
 to
to 
 i
i 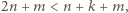 więc dwa z trzech składników licznika dzielą się przez
więc dwa z trzech składników licznika dzielą się przez 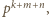 a trzeci nie, co oznacza, że liczba
a trzeci nie, co oznacza, że liczba 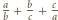 nie jest całkowita, wbrew założeniu.
nie jest całkowita, wbrew założeniu.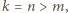 to
to 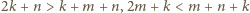 i
i 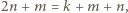 więc znów liczba
więc znów liczba 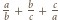 nie jest całkowita.
nie jest całkowita.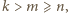 to
to 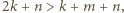
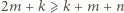 i
i 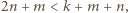 więc znów liczba
więc znów liczba 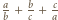 nie jest całkowita.
nie jest całkowita.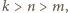 to
to 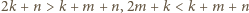 i
i  to teraz dwa składniki nie dzielą się przez
to teraz dwa składniki nie dzielą się przez  Ich suma może dzielić się przez
Ich suma może dzielić się przez 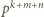 tylko wtedy, gdy
tylko wtedy, gdy 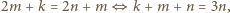 więc w tym wypadku liczba
więc w tym wypadku liczba 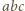 jest podzielna przez
jest podzielna przez 
 jest całkowita, to liczba pierwsza
jest całkowita, to liczba pierwsza  wchodzi w rozkład liczby
wchodzi w rozkład liczby 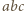 na czynniki pierwsze z wykładnikiem podzielnym przez
na czynniki pierwsze z wykładnikiem podzielnym przez 
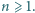 Niech
Niech  będzie ustalonym zbiorem
będzie ustalonym zbiorem 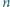 reszt z dzielenia przez
reszt z dzielenia przez  Udowodnić, że istnieje zbiór
Udowodnić, że istnieje zbiór 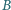 złożony z
złożony z 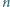 reszt z dzielenia przez
reszt z dzielenia przez 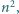 który spełnia następujący warunek: co najmniej połowa reszt z dzielenia przez
który spełnia następujący warunek: co najmniej połowa reszt z dzielenia przez 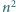 przystaje do liczby postaci
przystaje do liczby postaci 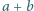 dla
dla  oraz
oraz 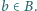
 niezależnych losowań ze zbioru reszt z dzielenia przez
niezależnych losowań ze zbioru reszt z dzielenia przez 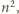 zakładając przy tym, że prawdopodobieństwo wylosowania dowolnej z reszt jest równe
zakładając przy tym, że prawdopodobieństwo wylosowania dowolnej z reszt jest równe 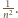 Z uzyskanych reszt tworzymy zbiór
Z uzyskanych reszt tworzymy zbiór  Ponieważ losowania są niezależne, może on składać się z mniej niż
Ponieważ losowania są niezależne, może on składać się z mniej niż 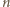 reszt, gdyż pewna reszta mogła zostać wylosowana więcej niż jeden raz. Jeżeli spełniony jest jednak warunek, w którym co najmniej połowa reszt może być zapisana w postaci
reszt, gdyż pewna reszta mogła zostać wylosowana więcej niż jeden raz. Jeżeli spełniony jest jednak warunek, w którym co najmniej połowa reszt może być zapisana w postaci 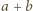 dla
dla 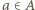 oraz
oraz 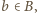 to możemy dopełnić zbiór
to możemy dopełnić zbiór  do zbioru
do zbioru  -elementowego w dowolny sposób i warunek ten pozostanie spełniony.
-elementowego w dowolny sposób i warunek ten pozostanie spełniony.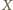 będzie liczbą reszt, które przystają do liczby postaci
będzie liczbą reszt, które przystają do liczby postaci 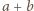 dla
dla 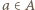 oraz
oraz  Wystarczy udowodnić, że wartość oczekiwana zmiennej losowej
Wystarczy udowodnić, że wartość oczekiwana zmiennej losowej  wynosi co najmniej
wynosi co najmniej 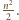 Ustalmy dowolną resztę
Ustalmy dowolną resztę 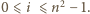 Ponieważ zbiór
Ponieważ zbiór 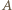 składa się z
składa się z  elementów, więc istnieje dokładnie
elementów, więc istnieje dokładnie  takich reszt
takich reszt 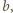 że
że  dla pewnego
dla pewnego 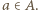 Prawdopodobieństwo tego, że ustalona reszta
Prawdopodobieństwo tego, że ustalona reszta 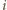 nie może być zapisana w żądanej postaci, wynosi zatem
nie może być zapisana w żądanej postaci, wynosi zatem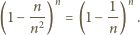
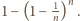 Korzystając z definicji wartości oczekiwanej oraz nierówności
Korzystając z definicji wartości oczekiwanej oraz nierówności 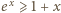 dla
dla 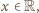 dostajemy
dostajemy![n2 ]=n2(1−(1−1))⩾n2(1−e−1)>n2(1−1)=n. E[X n22](/math/temat/matematyka/teoria_liczb/zadania/2015/03/29/zm-15_04-metody-4/19x-a985e63156cd220a3019db9f29340e69c1657a0c-dm-66,57,43-FF,FF,FF.gif)
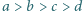 spełniają równanie
spełniają równanie
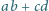 nie jest liczbą pierwszą.
nie jest liczbą pierwszą. Rozważmy taki czworokąt
Rozważmy taki czworokąt 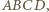 że
że 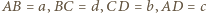 oraz
oraz 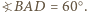 Z twierdzenia cosinusów zastosowanego do trójkątów
Z twierdzenia cosinusów zastosowanego do trójkątów 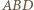 oraz
oraz 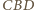 otrzymujemy wówczas
otrzymujemy wówczas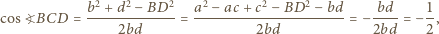
 miarę kąta
miarę kąta 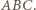 Wówczas
Wówczas 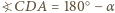 i korzystając z twierdzenia cosinusów tym razem w trójkątach
i korzystając z twierdzenia cosinusów tym razem w trójkątach  i
i 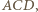 dostajemy
dostajemy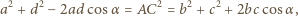
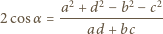
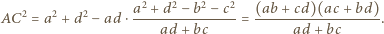
 jest wpisany w okrąg, to z twierdzenia Ptolemeusza wynika równość
jest wpisany w okrąg, to z twierdzenia Ptolemeusza wynika równość 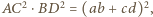 którą - korzystając z wcześniejszych obserwacji - możemy przepisać w postaci
którą - korzystając z wcześniejszych obserwacji - możemy przepisać w postaci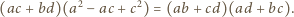
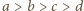 wynikają zależności
wynikają zależności 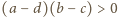 oraz
oraz  z których otrzymujemy ciąg nierówności
z których otrzymujemy ciąg nierówności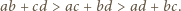
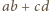 jest pierwsza, to biorąc pod uwagę powyższe nierówności, widzimy, że jest ona względnie pierwsza z liczbami
jest pierwsza, to biorąc pod uwagę powyższe nierówności, widzimy, że jest ona względnie pierwsza z liczbami 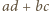 oraz
oraz  Z otrzymanej przez nas równości otrzymujemy więc podzielność
Z otrzymanej przez nas równości otrzymujemy więc podzielność 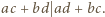 To jednak przeczy drugiej z powyższych nierówności i w efekcie dowodzi, że liczba
To jednak przeczy drugiej z powyższych nierówności i w efekcie dowodzi, że liczba  jest złożona.
jest złożona.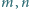 będą takimi dodatnimi liczbami całkowitymi, że w zbiorze
będą takimi dodatnimi liczbami całkowitymi, że w zbiorze 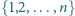 znajduje się dokładnie
znajduje się dokładnie 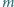 liczb pierwszych. Dowieść, że wśród dowolnych
liczb pierwszych. Dowieść, że wśród dowolnych 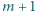 różnych liczb z tego zbioru można znaleźć liczbę, która jest dzielnikiem iloczynu pozostałych
różnych liczb z tego zbioru można znaleźć liczbę, która jest dzielnikiem iloczynu pozostałych  liczb.
liczb. oznacza sumę cyfr liczby całkowitej
oznacza sumę cyfr liczby całkowitej  w zapisie dziesiętnym. Dowieść, że istnieje nieskończenie wiele takich dodatnich liczb całkowitych
w zapisie dziesiętnym. Dowieść, że istnieje nieskończenie wiele takich dodatnich liczb całkowitych  że
że 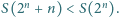
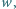 niebędąca liczbą całkowitą, że potęga
niebędąca liczbą całkowitą, że potęga 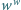 jest liczbą wymierną.
jest liczbą wymierną.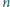 nazwiemy dobrą, jeżeli istnieje taka liczba pierwsza
nazwiemy dobrą, jeżeli istnieje taka liczba pierwsza 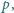 że liczba
że liczba  jest podzielna przez
jest podzielna przez 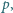 ale nie przez
ale nie przez 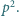 Wykazać, że wśród liczb
Wykazać, że wśród liczb 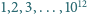 liczby dobre stanowią co najmniej
liczby dobre stanowią co najmniej 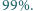
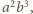 przy czym, oczywiście,
przy czym, oczywiście, 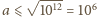 i
i 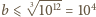 - jest tak ponieważ jeśli
- jest tak ponieważ jeśli 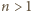 jest liczbą parzystą, to
jest liczbą parzystą, to 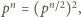 a jeśli
a jeśli 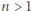 jest liczbą nieparzystą, to
jest liczbą nieparzystą, to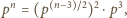
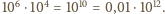
 będzie dowolną liczbą co najmniej dwucyfrową, której ostatnią cyfrą jest zero, a przedostatnią cyfrą nie jest dziewiątka. Wówczas w ciągu dwudziestu kolejnych liczb
będzie dowolną liczbą co najmniej dwucyfrową, której ostatnią cyfrą jest zero, a przedostatnią cyfrą nie jest dziewiątka. Wówczas w ciągu dwudziestu kolejnych liczb 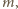
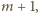 …,
…, 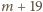 znajduje się liczba o sumie cyfr podzielnej przez 11; jeśli bowiem suma cyfr liczby
znajduje się liczba o sumie cyfr podzielnej przez 11; jeśli bowiem suma cyfr liczby  wynosi
wynosi 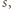 to sumy cyfr liczb
to sumy cyfr liczb  …,
…,  wynoszą
wynoszą 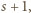 …,
…, 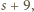 zaś liczba
zaś liczba  ma sumę cyfr równą
ma sumę cyfr równą 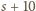 ; rzecz jasna, któraś z wartości
; rzecz jasna, któraś z wartości 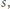
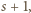 …,
…,  dzieli się przez 11.
dzieli się przez 11. postaci, jak wyżej.
postaci, jak wyżej. dla których równanie
dla których równanie 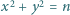 nie ma rozwiązań w liczbach całkowitych
nie ma rozwiązań w liczbach całkowitych 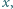
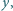 różnych od zera, ale ma rozwiązania w liczbach wymiernych
różnych od zera, ale ma rozwiązania w liczbach wymiernych 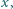
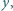 różnych od zera.
różnych od zera.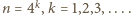 Żadna z nich nie jest sumą dwóch niezerowych kwadratów; przypuśćmy bowiem, że
Żadna z nich nie jest sumą dwóch niezerowych kwadratów; przypuśćmy bowiem, że  ; liczby
; liczby 
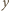 nie mogą być obie nieparzyste (bo wówczas
nie mogą być obie nieparzyste (bo wówczas 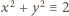 (mod 4)); muszą więc być parzyste, co daje przedstawienie liczby
(mod 4)); muszą więc być parzyste, co daje przedstawienie liczby 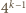 w postaci sumy dwóch niezerowych kwadratów. Dalsze zstępowanie prowadzi do konkluzji, że 4 jest sumą dwóch niezerowych kwadratów - a to absurd.
w postaci sumy dwóch niezerowych kwadratów. Dalsze zstępowanie prowadzi do konkluzji, że 4 jest sumą dwóch niezerowych kwadratów - a to absurd.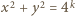 łatwo uzyskamy, biorąc dowolną trójkę pitagorejską liczb naturalnych
łatwo uzyskamy, biorąc dowolną trójkę pitagorejską liczb naturalnych  i przyjmując
i przyjmując 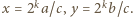
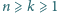 liczba
liczba

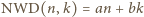 dla pewnych liczb całkowitych
dla pewnych liczb całkowitych
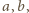 to
wystarczy udowodnić, że liczba
to
wystarczy udowodnić, że liczba
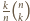 jest całkowita. Wynika to
z równości
jest całkowita. Wynika to
z równości
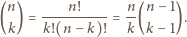
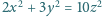 w zbiorze
liczb całkowitych jest
w zbiorze
liczb całkowitych jest
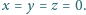
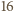 może dać tylko resztę 0 lub
może dać tylko resztę 0 lub
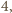 a kwadrat liczby
nieparzystej – resztę
a kwadrat liczby
nieparzystej – resztę
 lub
lub

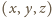 jest niezerowym rozwiązaniem.
Oczywiście,
jest niezerowym rozwiązaniem.
Oczywiście,
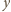 musi być parzyste, powiedzmy
musi być parzyste, powiedzmy
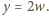 Wtedy
Wtedy
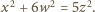 Możemy bez utraty ogólności założyć, że
Możemy bez utraty ogólności założyć, że
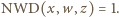 Ponieważ
Ponieważ
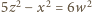 jest parzyste, to
mamy dwa przypadki:
jest parzyste, to
mamy dwa przypadki:
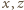 są parzyste;
są parzyste;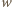 musi być nieparzyste (inaczej
musi być nieparzyste (inaczej
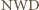 byłoby co najmniej 2).
Mamy
byłoby co najmniej 2).
Mamy
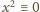 lub
lub
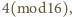
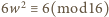 oraz
oraz
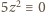 lub
lub
 Wtedy jednak liczby
Wtedy jednak liczby
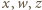 nie mogą spełniać równania
nie mogą spełniać równania
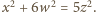
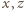 są nieparzyste;
są nieparzyste;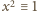 lub
lub
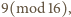
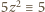 lub
lub
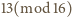 oraz
oraz
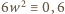 lub
lub
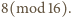 Nietrudno
sprawdzić, że ponownie liczby
Nietrudno
sprawdzić, że ponownie liczby
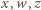 nie mogą spełniać
równania
nie mogą spełniać
równania
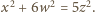
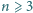 zachodzi
podzielność
zachodzi
podzielność
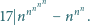
 zachodzi
zachodzi
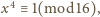 ponieważ
ponieważ
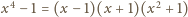 oraz
oraz
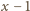 lub
lub
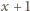 jest podzielne przez
jest podzielne przez
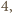 a pozostałe
czynniki są parzyste. Ponadto na mocy małego twierdzenia Fermata
a pozostałe
czynniki są parzyste. Ponadto na mocy małego twierdzenia Fermata
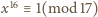 dla
dla
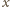 niepodzielnych przez
niepodzielnych przez
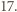 Zauważmy
jeszcze, że
Zauważmy
jeszcze, że
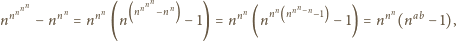
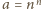 i
i

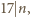 to teza jest oczywista. Niech więc
to teza jest oczywista. Niech więc
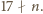 Jeśli
Jeśli
 jest parzyste, to
jest parzyste, to
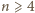 i mamy
i mamy
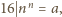 więc
więc

 jest nieparzyste, to
jest nieparzyste, to
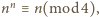 więc możemy
zapisać
więc możemy
zapisać
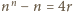 i wówczas
i wówczas
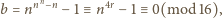
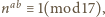 co daje tezę.
co daje tezę.
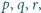 że liczba
że liczba
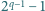 dzieli się przez
dzieli się przez
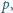 liczba
liczba
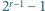 dzieli się przez
dzieli się przez
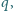 zaś liczba
zaś liczba
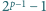 dzieli się przez
dzieli się przez
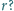
 liczba
liczba
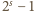 ma co
najmniej trzy różne dzielniki pierwsze
ma co
najmniej trzy różne dzielniki pierwsze
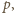
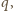
 Wykażemy,
że wówczas trójka
Wykażemy,
że wówczas trójka

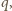
 spełnia postulowane
warunki.
spełnia postulowane
warunki.
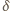 będzie najmniejszym wykładnikiem naturalnym, większym
od 1, dla którego
będzie najmniejszym wykładnikiem naturalnym, większym
od 1, dla którego
 (mod
(mod
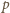 ). Z założenia także
). Z założenia także
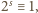 więc
więc
 dzieli się przez
dzieli się przez
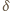 ; a skoro
; a skoro
 jest
liczbą pierwszą, to
jest
liczbą pierwszą, to
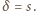 W myśl małego twierdzenia Fermata
W myśl małego twierdzenia Fermata
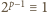 (mod
(mod
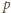 ), zatem
), zatem
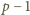 dzieli się przez
dzieli się przez
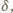 czyli
przez
czyli
przez
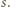
 jest dzielnikiem liczb
jest dzielnikiem liczb
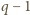 oraz
oraz
 Podnosząc kongruencję
Podnosząc kongruencję
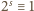 (mod
(mod
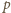 ) do potęgi
) do potęgi
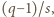 widzimy, że
widzimy, że
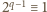 (mod
(mod
 ). Tak samo,
cyklicznie,
). Tak samo,
cyklicznie,
 (mod
(mod
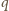 ),
),
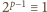 (mod
(mod
 ), czyli
mamy to, o co chodzi (a nawet więcej: okazuje się, że każda z liczb
), czyli
mamy to, o co chodzi (a nawet więcej: okazuje się, że każda z liczb
 dzieli się przez iloczyn
dzieli się przez iloczyn
 ).
).
 o podanej na wstępie własności.
Przeglądając tablicę liczb Mersenne’a znajdujemy w niej liczbę złożoną
o podanej na wstępie własności.
Przeglądając tablicę liczb Mersenne’a znajdujemy w niej liczbę złożoną
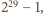 z rozkładem na czynniki pierwsze
z rozkładem na czynniki pierwsze
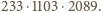 Zatem
liczby
Zatem
liczby

 tworzą jedną z trójek, jakich
szukamy.
tworzą jedną z trójek, jakich
szukamy.
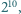 jest kwadratem liczby całkowitej? Podać wszystkie
rozwiązania (jeśli istnieją).
jest kwadratem liczby całkowitej? Podać wszystkie
rozwiązania (jeśli istnieją).
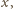
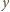 równania
równania
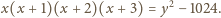
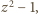 gdzie
gdzie
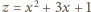 (skoro
(skoro
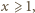 to
to
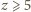 ) i rozwiązujemy równanie
) i rozwiązujemy równanie
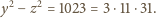
 w którym pierwszy
czynnik jest dodatni, więc drugi też. Musi to być iloczyn jednej z czterech
postaci:
w którym pierwszy
czynnik jest dodatni, więc drugi też. Musi to być iloczyn jednej z czterech
postaci:
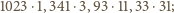
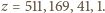 Jedynie
Jedynie
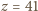 jest
wartością trójmianu
jest
wartością trójmianu
 dla naturalnego
dla naturalnego
 mianowicie
mianowicie
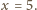 Otrzymujemy jedyne rozwiązanie zadania:
Otrzymujemy jedyne rozwiązanie zadania:
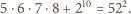
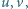 dla których liczba
dla których liczba

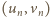 możemy uzyskać na przykład
biorąc ciąg Fibonacciego
możemy uzyskać na przykład
biorąc ciąg Fibonacciego
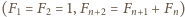 i określając
i określając
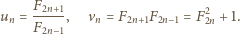
 mamy wówczas
mamy wówczas
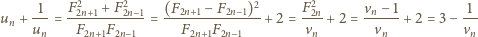
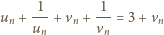
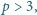 taka, że
taka, że
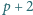 też jest pierwsza.
Na tablicy napisano liczby
też jest pierwsza.
Na tablicy napisano liczby
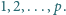 W każdym kroku wybieramy
jedną z nich, powiedzmy
W każdym kroku wybieramy
jedną z nich, powiedzmy
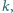 po czym zmazujemy wszystkie dzielniki
liczby
po czym zmazujemy wszystkie dzielniki
liczby
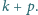 Udowodnić, że w ten sposób nigdy nie zmażemy
wszystkich liczb napisanych na tablicy.
Udowodnić, że w ten sposób nigdy nie zmażemy
wszystkich liczb napisanych na tablicy.
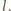 Skoro została ona zmazana, to
Skoro została ona zmazana, to
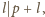 czyli również
czyli również
 a zatem
a zatem
 lub
lub

 i
i
 będą odpowiednio liczbami wybranymi w pierwszym i drugim kroku.
Ponieważ liczba 1 zniknęła z tablicy po pierwszym kroku, więc
będą odpowiednio liczbami wybranymi w pierwszym i drugim kroku.
Ponieważ liczba 1 zniknęła z tablicy po pierwszym kroku, więc
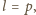 co oznacza, że po pierwszym kroku na tablicy były wyłącznie liczby
co oznacza, że po pierwszym kroku na tablicy były wyłącznie liczby
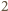 i
i
 lub tylko
lub tylko
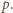 Ponieważ
Ponieważ
 więc
więc
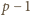 zmazaliśmy w pierwszym kroku, a zatem
zmazaliśmy w pierwszym kroku, a zatem
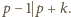 Natomiast z nierówności
Natomiast z nierówności
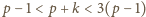 wynika, że
wynika, że
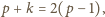 czyli
czyli
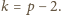 Ale
Ale
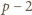 też musiało
zostać zmazane w pierwszym kroku, więc
też musiało
zostać zmazane w pierwszym kroku, więc
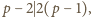 co jest
niemożliwe.
co jest
niemożliwe.
 Ta liczba nie została zmazana w tym
kroku, gdyż
Ta liczba nie została zmazana w tym
kroku, gdyż
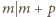 oznacza, że
oznacza, że
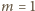 lub
lub
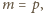 ale 1
zniknęła w pierwszym kroku, a
ale 1
zniknęła w pierwszym kroku, a
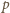 musi być wybrane w ostatnim. Zatem
musi być wybrane w ostatnim. Zatem
 zmazujemy w ostatnim kroku, czyli
zmazujemy w ostatnim kroku, czyli
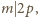 więc
więc
 Wobec tego w przedostatnim kroku mogliśmy wymazać tylko dzielniki liczby
Wobec tego w przedostatnim kroku mogliśmy wymazać tylko dzielniki liczby
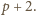 Ale ta liczba jest pierwsza, więc nie wymazaliśmy nic, co daje
sprzeczność.
Ale ta liczba jest pierwsza, więc nie wymazaliśmy nic, co daje
sprzeczność.
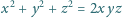
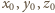 to liczby całkowite dodatnie, takie
że
to liczby całkowite dodatnie, takie
że
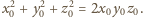 Ponieważ prawa strona jest liczbą parzystą, to
dokładnie dwie z liczb
Ponieważ prawa strona jest liczbą parzystą, to
dokładnie dwie z liczb
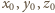 są nieparzyste lub żadna nieparzysta nie
jest. Pierwszy przypadek nie może mieć miejsca, gdyż wówczas lewa strona
przy dzieleniu przez
są nieparzyste lub żadna nieparzysta nie
jest. Pierwszy przypadek nie może mieć miejsca, gdyż wówczas lewa strona
przy dzieleniu przez
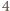 dałaby resztę
dałaby resztę
 zaś prawa
zaś prawa
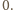 Dlatego
Dlatego
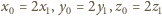 dla pewnych liczb całkowitych dodatnich
dla pewnych liczb całkowitych dodatnich
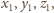 mniejszych od
mniejszych od
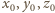 odpowiednio. Po wstawieniu do
równania otrzymujemy zależność
odpowiednio. Po wstawieniu do
równania otrzymujemy zależność
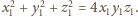 Powtarzając
całe rozumowanie, dostajemy malejące ciągi liczb całkowitych dodatnich
Powtarzając
całe rozumowanie, dostajemy malejące ciągi liczb całkowitych dodatnich
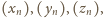 przy czym
przy czym
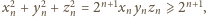 co jest
niemożliwe.
co jest
niemożliwe.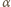 oraz prawdziwa jest implikacja
oraz prawdziwa jest implikacja
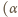 to
to
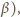 to
prawdziwe jest też zdanie
to
prawdziwe jest też zdanie
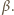 Można sobie przecież wyobrazić, że
długość dowodu formuły
Można sobie przecież wyobrazić, że
długość dowodu formuły
 jak i długość dowodu implikacji
jak i długość dowodu implikacji
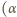 to
to
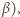 są dostępnymi liczbami naturalnymi, a ich suma już
nie.
są dostępnymi liczbami naturalnymi, a ich suma już
nie.
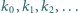 taki, że dla każdego
taki, że dla każdego
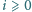 iloczyn
iloczyn
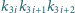 jest
podzielny przez każdą z liczb
jest
podzielny przez każdą z liczb
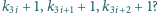
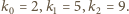 Przyjmijmy, że wyrazy
Przyjmijmy, że wyrazy
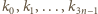 są
już określone i tworzą ciąg rosnący długości
są
już określone i tworzą ciąg rosnący długości
 spełniający
wymagany warunek. Oznaczmy dla wygody:
spełniający
wymagany warunek. Oznaczmy dla wygody:
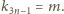 Określamy
kolejne trzy wyrazy:
Określamy
kolejne trzy wyrazy:

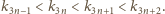 Pozostaje sprawdzić, że iloczyn
trzech wypisanych liczb, równy
Pozostaje sprawdzić, że iloczyn
trzech wypisanych liczb, równy
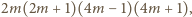 dzieli się
przez każdą z tych liczb, powiększoną o 1, czyli przez liczby
dzieli się
przez każdą z tych liczb, powiększoną o 1, czyli przez liczby
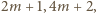
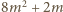 ; a to jest oczywiste. Kontynuując, otrzymujemy nieskończony
ciąg
; a to jest oczywiste. Kontynuując, otrzymujemy nieskończony
ciąg
 o żądanych własnościach.
o żądanych własnościach.