Zadanie ZM-1307
o zadaniu...
- Publikacja w Delcie: marzec 2011
- Publikacja elektroniczna: 02-03-2011
Udowodnić, że spośród dowolnych
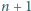 liczb ze zbioru
liczb ze zbioru
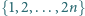 można wybrać dwie, tak żeby jedna była
dzielnikiem drugiej.
można wybrać dwie, tak żeby jedna była
dzielnikiem drugiej.
Udowodnić, że spośród dowolnych
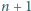 liczb ze zbioru
liczb ze zbioru
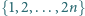 można wybrać dwie, tak żeby jedna była
dzielnikiem drugiej.
można wybrać dwie, tak żeby jedna była
dzielnikiem drugiej.
Dane są liczby całkowite dodatnie
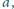
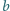 o następującej własności:
o następującej własności:
dla każdej liczby całkowitej dodatniej
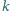 liczby
liczby
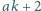 oraz
oraz
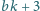 nie są względnie pierwsze. Udowodnić, że
nie są względnie pierwsze. Udowodnić, że
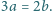
Rozwiązać równanie
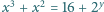 w liczbach całkowitych
w liczbach całkowitych
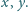
Udowodnij, że nie istnieją liczby nieparzyste
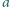 i
i
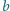 spełniające
równanie
spełniające
równanie
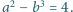
Czy istnieją różne liczby pierwsze
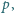
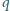 i
i
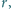 dla których
liczba
dla których
liczba
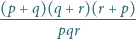
jest liczbą całkowitą? Odpowiedź uzasadnij.
Zadanie 610 zaproponował pan Michał Kieza z Warszawy.
Ciąg
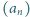 jest określony rekurencyjnie:
jest określony rekurencyjnie:
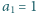 ,
,
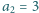 ,
,
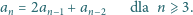
Dowieść, że żaden wyraz tego ciągu nie ma dzielnika dodatniego
postaci
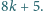
Niech
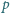 będzie liczbą pierwszą postaci
będzie liczbą pierwszą postaci
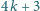 . Dowieść, że
zbioru złożonego z
. Dowieść, że
zbioru złożonego z
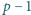 kolejnych liczb całkowitych nie da się
podzielić na dwa podzbiory w taki sposób, aby iloczyn liczb w jednym
podzbiorze był równy iloczynowi liczb w drugim podzbiorze.
kolejnych liczb całkowitych nie da się
podzielić na dwa podzbiory w taki sposób, aby iloczyn liczb w jednym
podzbiorze był równy iloczynowi liczb w drugim podzbiorze.
Wyznaczyć wszystkie liczby całkowite dodatnie
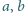 , dla których liczba
, dla których liczba
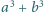 jest czwartą potęgą liczby pierwszej.
jest czwartą potęgą liczby pierwszej.
Niech
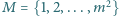 , gdzie
, gdzie
 jest ustaloną liczbą naturalną.
jest ustaloną liczbą naturalną.
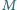 podzbiorów niezawierających pary liczb,
których różnica dzieli się przez
podzbiorów niezawierających pary liczb,
których różnica dzieli się przez
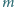 ?
?
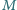 podzbiorów niezawierających pary liczb,
których różnica jest
równa
podzbiorów niezawierających pary liczb,
których różnica jest
równa
 ?
?Zadanie zaproponował pan Paweł Kubit z Krakowa.
Dowieść, że dla każdej liczby naturalnej
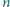 istnieje taki ciąg
arytmetyczny liczb naturalnych
istnieje taki ciąg
arytmetyczny liczb naturalnych
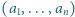 oraz taki ciąg geometryczny
liczb naturalnych
oraz taki ciąg geometryczny
liczb naturalnych
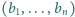 , że
, że

Wyznaczyć najmniejszą liczbą naturalną, której nie da się przedstawić w postaci

gdzie
 ,
,
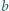 ,
,
 ,
,
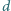 są liczbami całkowitymi dodatnimi.
są liczbami całkowitymi dodatnimi.
Rozstrzygnąć, czy istnieje 19-cyfrowa liczba naturalna N podzielna przez 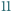 o tej własności, że każda inna 19-cyfrowa liczba otrzymana z N poprzez zmianę kolejności (permutację) jej cyfr nie jest podzielna przez
o tej własności, że każda inna 19-cyfrowa liczba otrzymana z N poprzez zmianę kolejności (permutację) jej cyfr nie jest podzielna przez