Przyjmijmy oznaczenia: 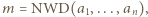
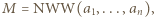
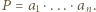 Wystarczy wykazać, że każda liczba pierwsza, która dzieli iloczyn
Wystarczy wykazać, że każda liczba pierwsza, która dzieli iloczyn 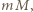 wchodzi do iloczynu
wchodzi do iloczynu 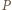 w co najmniej takiej samej potędze. Niech więc
w co najmniej takiej samej potędze. Niech więc 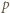 będzie liczbą pierwszą i niech (dla
będzie liczbą pierwszą i niech (dla 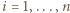 )
) 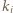 będzie takim wykładnikiem, że
będzie takim wykładnikiem, że 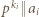 (ten napis oznacza, że
(ten napis oznacza, że 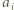 dzieli się przez
dzieli się przez 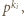 ale nie przez
ale nie przez 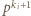 ). Wówczas
). Wówczas 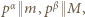 gdzie
gdzie 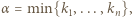
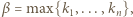 i wobec tego
i wobec tego 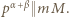 Oczywiście
Oczywiście 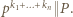 Porównanie wykładników nie pozostawia wątpliwości:
Porównanie wykładników nie pozostawia wątpliwości:
 |
(1) |
Wobec dowolności wyboru 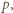 uzasadnia to zadaną nierówność
uzasadnia to zadaną nierówność 
Kiedy zachodzi równość 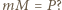 Wtedy, gdy każda liczba pierwsza dzieli
Wtedy, gdy każda liczba pierwsza dzieli 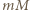 w dokładnie tej samej potędze, w jakiej dzieli
w dokładnie tej samej potędze, w jakiej dzieli 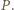 Czyli gdy dla każdej liczby pierwszej
Czyli gdy dla każdej liczby pierwszej 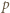 nierówność (1) (z wykładnikami
nierówność (1) (z wykładnikami 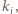 wyznaczonymi przez
wyznaczonymi przez 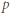 ) staje się równością.
) staje się równością.
Dla 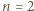 jest tak zawsze; dostajemy znaną tożsamość:
jest tak zawsze; dostajemy znaną tożsamość: 
Dla 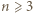 równość w relacji (1) oznacza, że gdy po jej prawej stronie usuniemy jeden największy i jeden najmniejszy składnik, pozostaną jakieś nieskreślone składniki, o zerowej sumie - czyli wszystkie równe zeru. Składnik najmniejszy automatycznie także jest zerem. Tylko jeden składnik po prawej stronie (1) może być dodatni. To znaczy, że tylko jedna z liczb
równość w relacji (1) oznacza, że gdy po jej prawej stronie usuniemy jeden największy i jeden najmniejszy składnik, pozostaną jakieś nieskreślone składniki, o zerowej sumie - czyli wszystkie równe zeru. Składnik najmniejszy automatycznie także jest zerem. Tylko jeden składnik po prawej stronie (1) może być dodatni. To znaczy, że tylko jedna z liczb 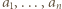 może dzielić się przez
może dzielić się przez 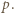 Wobec dowolności
Wobec dowolności 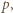 znaczy to, że liczby
znaczy to, że liczby 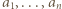 są parami względnie pierwsze.
są parami względnie pierwsze.
I na odwrót, gdy tak jest, wówczas dla każdej liczby pierwszej 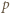 mamy w ciągu
mamy w ciągu 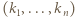 co najwyżej jeden wyraz niezerowy; nierównść (1) przechodzi w równość, i w konsekwencji
co najwyżej jeden wyraz niezerowy; nierównść (1) przechodzi w równość, i w konsekwencji 
Podsumowując: dla 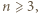 równość
równość 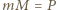 zachodzi wtedy i tylko wtedy, gdy liczby
zachodzi wtedy i tylko wtedy, gdy liczby 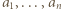 są parami względnie pierwsze; dla
są parami względnie pierwsze; dla 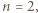 ta równość jest tożsamością.
ta równość jest tożsamością.
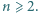 Wykazać, że dla każdego układu dodatnich liczb całkowitych
Wykazać, że dla każdego układu dodatnich liczb całkowitych 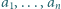 zachodzi nierówność
zachodzi nierówność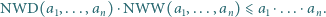
 ) te układy
) te układy 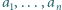 (dodatnich liczb całkowitych), dla których napisana nierówność staje się równością.
(dodatnich liczb całkowitych), dla których napisana nierówność staje się równością.
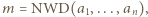
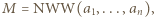
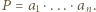 Wystarczy wykazać, że każda liczba pierwsza, która dzieli iloczyn
Wystarczy wykazać, że każda liczba pierwsza, która dzieli iloczyn 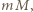 wchodzi do iloczynu
wchodzi do iloczynu 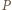 w co najmniej takiej samej potędze. Niech więc
w co najmniej takiej samej potędze. Niech więc 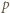 będzie liczbą pierwszą i niech (dla
będzie liczbą pierwszą i niech (dla 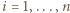 )
) 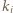 będzie takim wykładnikiem, że
będzie takim wykładnikiem, że 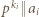 (ten napis oznacza, że
(ten napis oznacza, że 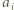 dzieli się przez
dzieli się przez 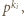 ale nie przez
ale nie przez 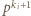 ). Wówczas
). Wówczas 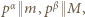 gdzie
gdzie 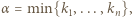
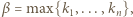 i wobec tego
i wobec tego 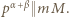 Oczywiście
Oczywiście 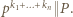 Porównanie wykładników nie pozostawia wątpliwości:
Porównanie wykładników nie pozostawia wątpliwości:
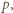 uzasadnia to zadaną nierówność
uzasadnia to zadaną nierówność 
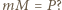 Wtedy, gdy każda liczba pierwsza dzieli
Wtedy, gdy każda liczba pierwsza dzieli 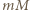 w dokładnie tej samej potędze, w jakiej dzieli
w dokładnie tej samej potędze, w jakiej dzieli 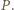 Czyli gdy dla każdej liczby pierwszej
Czyli gdy dla każdej liczby pierwszej 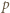 nierówność (1) (z wykładnikami
nierówność (1) (z wykładnikami 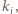 wyznaczonymi przez
wyznaczonymi przez 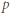 ) staje się równością.
) staje się równością.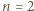 jest tak zawsze; dostajemy znaną tożsamość:
jest tak zawsze; dostajemy znaną tożsamość: 
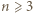 równość w relacji (1) oznacza, że gdy po jej prawej stronie usuniemy jeden największy i jeden najmniejszy składnik, pozostaną jakieś nieskreślone składniki, o zerowej sumie - czyli wszystkie równe zeru. Składnik najmniejszy automatycznie także jest zerem. Tylko jeden składnik po prawej stronie (1) może być dodatni. To znaczy, że tylko jedna z liczb
równość w relacji (1) oznacza, że gdy po jej prawej stronie usuniemy jeden największy i jeden najmniejszy składnik, pozostaną jakieś nieskreślone składniki, o zerowej sumie - czyli wszystkie równe zeru. Składnik najmniejszy automatycznie także jest zerem. Tylko jeden składnik po prawej stronie (1) może być dodatni. To znaczy, że tylko jedna z liczb 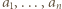 może dzielić się przez
może dzielić się przez 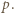 Wobec dowolności
Wobec dowolności 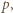 znaczy to, że liczby
znaczy to, że liczby 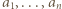 są parami względnie pierwsze.
są parami względnie pierwsze.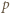 mamy w ciągu
mamy w ciągu 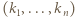 co najwyżej jeden wyraz niezerowy; nierównść (1) przechodzi w równość, i w konsekwencji
co najwyżej jeden wyraz niezerowy; nierównść (1) przechodzi w równość, i w konsekwencji 
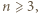 równość
równość 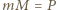 zachodzi wtedy i tylko wtedy, gdy liczby
zachodzi wtedy i tylko wtedy, gdy liczby 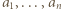 są parami względnie pierwsze; dla
są parami względnie pierwsze; dla 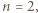 ta równość jest tożsamością.
ta równość jest tożsamością.