Eksperymenty z niewielkimi wartościami
 pozwalają zgadnąć, że
szukaną wielokrotnością liczby
pozwalają zgadnąć, że
szukaną wielokrotnością liczby
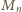 jest iloczyn
jest iloczyn
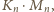 gdzie
gdzie
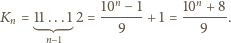
Rzeczywiście, iloczyn
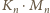 nie ma dziewiątki w zapisie dziesiętnym:
nie ma dziewiątki w zapisie dziesiętnym:
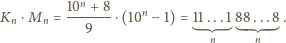
Należy teraz wykazać, że dziewiątka występuje w każdym z iloczynów
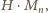 gdy
gdy
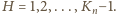
Niech
 będzie liczbą
będzie liczbą
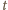 -cyfrową:
-cyfrową:
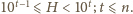 Bierzemy
iloczyn
Bierzemy
iloczyn
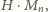 skreślamy jego końcowe
skreślamy jego końcowe
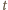 cyfr i dostajemy
liczbę
cyfr i dostajemy
liczbę
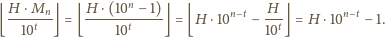
Jeżeli
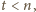 uzyskana liczba ma dziewiątkę na końcu; również
wtedy, gdy
uzyskana liczba ma dziewiątkę na końcu; również
wtedy, gdy
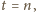 zaś
zaś
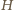 kończy się zerem. To znaczy, że
w tych przypadkach iloczyn
kończy się zerem. To znaczy, że
w tych przypadkach iloczyn
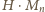 ma dziewiątkę w rzędzie
ma dziewiątkę w rzędzie
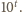
Pamiętając, że rozważamy
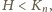 pozostaje rozpatrzeć sytuacje,
gdy
pozostaje rozpatrzeć sytuacje,
gdy
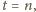 przy czym albo
przy czym albo
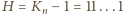 (wówczas
(wówczas
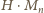 ma dziewiątkę na końcu), albo
ma dziewiątkę na końcu), albo
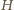 ma w zapisie
dziesiętnym co najmniej jedno zero, ale nie na pozycji końcowej. Ma
więc postać
ma w zapisie
dziesiętnym co najmniej jedno zero, ale nie na pozycji końcowej. Ma
więc postać
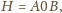 gdzie zero rozdziela dwie niepuste grupy
cyfr. Przyjmijmy, że
gdzie zero rozdziela dwie niepuste grupy
cyfr. Przyjmijmy, że
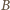 jest grupą
jest grupą
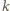 -cyfrową; oczywiście
-cyfrową; oczywiście
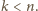 W myśl rozpatrzonego już przypadku, iloczyn
W myśl rozpatrzonego już przypadku, iloczyn
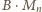 ma
dziewiątkę w rzędzie
ma
dziewiątkę w rzędzie
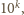 czyli właśnie na tej pozycji, na której
czyli właśnie na tej pozycji, na której
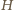 ma zero. Ta dziewiątka pozostanie obecna w iloczynie
ma zero. Ta dziewiątka pozostanie obecna w iloczynie
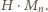
Zatem, istotnie,
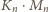 jest najmniejszą wielokrotnością liczby
jest najmniejszą wielokrotnością liczby
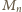 bez dziewiątki w zapisie dziesiętnym.
bez dziewiątki w zapisie dziesiętnym.
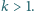 Znaleźć wszystkie liczby naturalne
Znaleźć wszystkie liczby naturalne
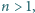 spełniające nierówność
spełniające nierówność

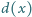 oznacza liczbę dodatnich dzielników liczby naturalnej
oznacza liczbę dodatnich dzielników liczby naturalnej

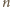 ma co najmniej dwa różne dzielniki pierwsze
ma co najmniej dwa różne dzielniki pierwsze
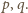 Napiszmy
Napiszmy
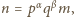 gdzie
gdzie
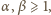 zaś czynnik
zaś czynnik
 jest niepodzielny przez
jest niepodzielny przez
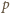 ani
ani
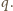 Iloczyn
Iloczyn
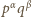 ma
ma
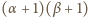 dzielników dodatnich; iloczyn
dzielników dodatnich; iloczyn
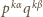 ma
ma
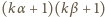 dzielników dodatnich. Zatem
dzielników dodatnich. Zatem
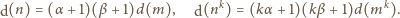
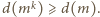 Jeśli więc zachodzi postulowana nierówność
Jeśli więc zachodzi postulowana nierówność
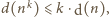 to
to
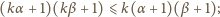
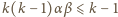 ; a to jest niemożliwe, skoro
; a to jest niemożliwe, skoro
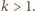
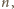 będące potęgami liczb
pierwszych. Każda taka liczba spełnia wymagany warunek; jeśli bowiem
będące potęgami liczb
pierwszych. Każda taka liczba spełnia wymagany warunek; jeśli bowiem
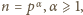 to
to
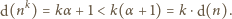
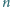 i liczby całkowite dodatnie względnie
pierwsze
i liczby całkowite dodatnie względnie
pierwsze
 i
i
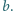 Udowodnić, że liczba
Udowodnić, że liczba
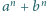 jest
podzielna przez
jest
podzielna przez
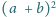 wtedy i tylko wtedy, gdy liczba
wtedy i tylko wtedy, gdy liczba
 jest
podzielna przez
jest
podzielna przez
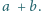
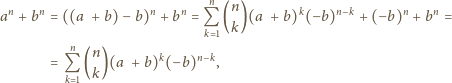
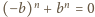 dla nieparzystych
dla nieparzystych
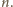 Zatem
Zatem
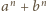 przy dzieleniu przez
przy dzieleniu przez
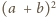 daje taką samą resztę jak
składnik odpowiadający
daje taką samą resztę jak
składnik odpowiadający
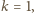 który wynosi
który wynosi
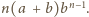 Zatem
Zatem
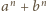 jest podzielne przez
jest podzielne przez
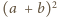 wtedy i tylko wtedy, gdy
wtedy i tylko wtedy, gdy
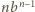 jest podzielne przez
jest podzielne przez
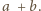 Ponieważ
Ponieważ
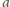 i
i
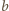 są
względnie pierwsze, względnie pierwsze są również
są
względnie pierwsze, względnie pierwsze są również
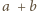 i
i
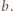 Stąd
otrzymujemy tezę.
Stąd
otrzymujemy tezę.
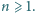 Niech
Niech
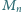 będzie liczbą
naturalną, której zapis dziesiętny składa się z
będzie liczbą
naturalną, której zapis dziesiętny składa się z
 dziewiątek:
dziewiątek:
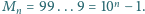 Znaleźć najmniejszą jej wielokrotność,
w której zapisie dziesiętnym cyfra 9 nie występuje.
Znaleźć najmniejszą jej wielokrotność,
w której zapisie dziesiętnym cyfra 9 nie występuje.
 pozwalają zgadnąć, że
szukaną wielokrotnością liczby
pozwalają zgadnąć, że
szukaną wielokrotnością liczby
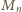 jest iloczyn
jest iloczyn
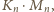 gdzie
gdzie
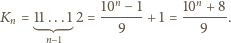
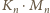 nie ma dziewiątki w zapisie dziesiętnym:
nie ma dziewiątki w zapisie dziesiętnym:
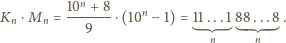
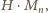 gdy
gdy
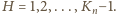
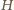 będzie liczbą
będzie liczbą
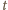 -cyfrową:
-cyfrową:
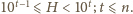 Bierzemy
iloczyn
Bierzemy
iloczyn
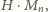 skreślamy jego końcowe
skreślamy jego końcowe
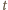 cyfr i dostajemy
liczbę
cyfr i dostajemy
liczbę
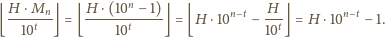
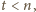 uzyskana liczba ma dziewiątkę na końcu; również
wtedy, gdy
uzyskana liczba ma dziewiątkę na końcu; również
wtedy, gdy
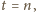 zaś
zaś
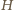 kończy się zerem. To znaczy, że
w tych przypadkach iloczyn
kończy się zerem. To znaczy, że
w tych przypadkach iloczyn
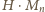 ma dziewiątkę w rzędzie
ma dziewiątkę w rzędzie
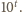
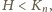 pozostaje rozpatrzeć sytuacje,
gdy
pozostaje rozpatrzeć sytuacje,
gdy
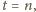 przy czym albo
przy czym albo
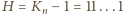 (wówczas
(wówczas
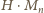 ma dziewiątkę na końcu), albo
ma dziewiątkę na końcu), albo
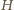 ma w zapisie
dziesiętnym co najmniej jedno zero, ale nie na pozycji końcowej. Ma
więc postać
ma w zapisie
dziesiętnym co najmniej jedno zero, ale nie na pozycji końcowej. Ma
więc postać
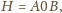 gdzie zero rozdziela dwie niepuste grupy
cyfr. Przyjmijmy, że
gdzie zero rozdziela dwie niepuste grupy
cyfr. Przyjmijmy, że
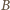 jest grupą
jest grupą
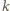 -cyfrową; oczywiście
-cyfrową; oczywiście
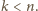 W myśl rozpatrzonego już przypadku, iloczyn
W myśl rozpatrzonego już przypadku, iloczyn
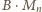 ma
dziewiątkę w rzędzie
ma
dziewiątkę w rzędzie
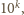 czyli właśnie na tej pozycji, na której
czyli właśnie na tej pozycji, na której
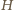 ma zero. Ta dziewiątka pozostanie obecna w iloczynie
ma zero. Ta dziewiątka pozostanie obecna w iloczynie
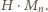
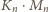 jest najmniejszą wielokrotnością liczby
jest najmniejszą wielokrotnością liczby
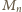 bez dziewiątki w zapisie dziesiętnym.
bez dziewiątki w zapisie dziesiętnym.
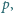 dla której
dla której
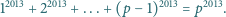
 zachodzi
zachodzi
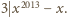 Stąd
Stąd
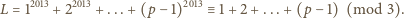
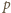 jest postaci
jest postaci
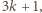 to wówczas
to wówczas
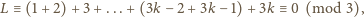
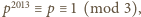 więc równanie nie ma rozwiązania
w tym przypadku. Podobnie stwierdzamy, że dla
więc równanie nie ma rozwiązania
w tym przypadku. Podobnie stwierdzamy, że dla
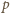 postaci
postaci
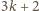 równanie jest sprzeczne. Zatem jedyna możliwość to
równanie jest sprzeczne. Zatem jedyna możliwość to
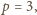 ale łatwo sprawdzić, że wtedy równanie również jest
sprzeczne.
ale łatwo sprawdzić, że wtedy równanie również jest
sprzeczne.
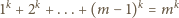
 oraz
oraz
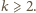 Dziś
wiadomo, że jeśli równanie ma rozwiązanie dla jakiegoś
Dziś
wiadomo, że jeśli równanie ma rozwiązanie dla jakiegoś
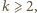 to
to
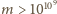 (zgrabny dowód i historia problemu są przedstawione
w artykule: P. Moore, A top hat for Moser’s four mathemagical rabbits, Amer.
Math. Monthly 118 (2011), 364-370).
(zgrabny dowód i historia problemu są przedstawione
w artykule: P. Moore, A top hat for Moser’s four mathemagical rabbits, Amer.
Math. Monthly 118 (2011), 364-370).
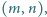 dla których
liczby
dla których
liczby

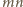 powinien być dzielnikiem liczb
powinien być dzielnikiem liczb
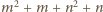 oraz
oraz
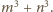 Zatem
Zatem
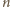 ma być dzielnikiem liczb
ma być dzielnikiem liczb
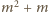 oraz
oraz
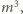 więc także liczby
więc także liczby
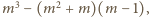 równej
równej
 Przez symetrię, liczba
Przez symetrię, liczba
 ma być dzielnikiem liczby
ma być dzielnikiem liczby
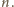 Dostajemy warunek
Dostajemy warunek
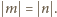
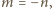 podane w zadaniu sumy wynoszą
podane w zadaniu sumy wynoszą
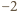 oraz 0
(więc są całkowite). Jeśli zaś
oraz 0
(więc są całkowite). Jeśli zaś
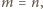 wynoszą one odpowiednio
wynoszą one odpowiednio
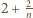 oraz
oraz
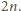 Są one obie całkowite wtedy i tylko wtedy, gdy
Są one obie całkowite wtedy i tylko wtedy, gdy
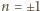 lub
lub
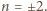
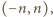 gdzie
gdzie
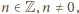 a ponadto cztery pary
a ponadto cztery pary
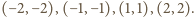
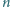 będzie liczbą pięciocyfrową w zapisie dziesiętnym (pierwsza
cyfra jest różna od
będzie liczbą pięciocyfrową w zapisie dziesiętnym (pierwsza
cyfra jest różna od
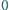 ) i niech
) i niech
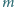 będzie liczbą czterocyfrową
powstałą z
będzie liczbą czterocyfrową
powstałą z
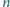 przez wyrzucenie jej środkowej cyfry. Znaleźć wszystkie
takie liczby
przez wyrzucenie jej środkowej cyfry. Znaleźć wszystkie
takie liczby
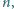 że liczba
że liczba
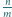 jest całkowita.
jest całkowita.
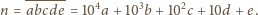
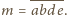 Załóżmy, że
Załóżmy, że
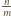 jest liczbą całkowitą.
Gdyby było
jest liczbą całkowitą.
Gdyby było
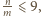 to przyjmując oznaczenia
to przyjmując oznaczenia
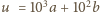 oraz
oraz
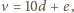 mielibyśmy
mielibyśmy
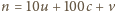 i
i
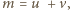 a stąd
sprzeczność:
a stąd
sprzeczność:
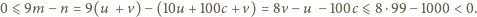
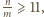 to
to
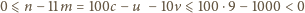
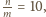 co daje
co daje
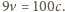 Stąd,
gdyby
Stąd,
gdyby
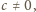 liczba
liczba
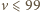 byłaby podzielna przez 100. Wobec tego
byłaby podzielna przez 100. Wobec tego
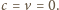 Wtedy mamy
Wtedy mamy
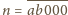 – wówczas
– wówczas

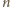 postaci
postaci
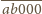 są wszystkimi liczbami
pięciocyfrowymi o własności z treści zadania.
są wszystkimi liczbami
pięciocyfrowymi o własności z treści zadania.
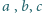 takie, że
takie, że
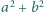 dzieli się przez
dzieli się przez

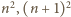 będą końcami danego przedziału. Wymagane warunki
spełniają na przykład liczby
będą końcami danego przedziału. Wymagane warunki
spełniają na przykład liczby
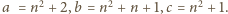 Rzeczywiście,
Rzeczywiście,
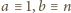 (mod
(mod
 ), więc
), więc
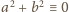 (mod
(mod
 ).
).
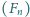 będzie ciągiem Fibonacciego:
będzie ciągiem Fibonacciego:

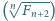 jest malejący.
jest malejący.
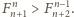 Dla
Dla
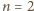 to prawda
to prawda
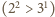 . Dalej przyjmujemy
. Dalej przyjmujemy
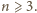 Korzystamy ze wzoru
Korzystamy ze wzoru
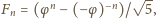 gdzie
gdzie
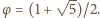 Oznaczmy:
Oznaczmy:
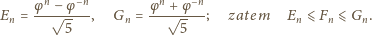
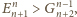 czyli
czyli
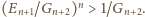 A ponieważ
A ponieważ
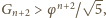 wystarczy dowieść, że
wystarczy dowieść, że
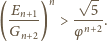
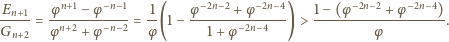
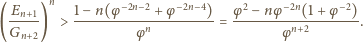
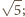 jest to równoważne nierówności
jest to równoważne nierówności
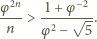
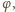 sprawdzamy, że nierówność (2)
zachodzi dla
sprawdzamy, że nierówność (2)
zachodzi dla
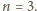 Zachodzi więc dla wszystkich
Zachodzi więc dla wszystkich
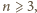 bo
wyrażenie po lewej stronie (2) przedstawia ciąg rosnący. To kończy
dowód.
bo
wyrażenie po lewej stronie (2) przedstawia ciąg rosnący. To kończy
dowód.
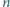 jest dodatnią liczbą całkowitą, to liczba
jest dodatnią liczbą całkowitą, to liczba
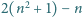 nie jest kwadratem liczby całkowitej.
nie jest kwadratem liczby całkowitej.
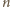 przez
przez
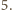 Dla
Dla
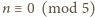 lub
lub
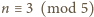 mamy
mamy
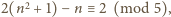 a więc
a więc
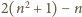 nie może być kwadratem liczby całkowitej.
Podobnie dla
nie może być kwadratem liczby całkowitej.
Podobnie dla
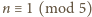 lub
lub
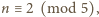 liczba
liczba
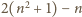 nie może być kwadratem liczby całkowitej, bo
nie może być kwadratem liczby całkowitej, bo
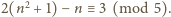 Przypuśćmy zatem, że
Przypuśćmy zatem, że
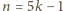 dla
pewnego
dla
pewnego
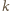 całkowitego. Wówczas
całkowitego. Wówczas
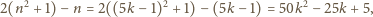
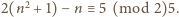 Zatem liczba
Zatem liczba
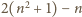 jest
podzielna przez
jest
podzielna przez
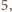 ale nie jest podzielna przez
ale nie jest podzielna przez
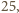 czyli i ona nie
może być kwadratem liczby całkowitej.
czyli i ona nie
może być kwadratem liczby całkowitej.
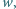 niebędąca
liczbą całkowitą, że potęga
niebędąca
liczbą całkowitą, że potęga
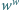 jest liczbą wymierną
jest liczbą wymierną
 istnieje i zapiszmy ją w postaci
nieskracalnego ułamka
istnieje i zapiszmy ją w postaci
nieskracalnego ułamka
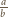 o dodatnim liczniku i mianowniku. Dla
dowolnych liczb całkowitych
o dodatnim liczniku i mianowniku. Dla
dowolnych liczb całkowitych
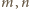 liczba
liczba
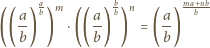
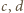
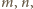
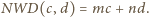
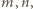 że
że
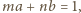 zatem
liczba
zatem
liczba
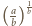 jest wymierna. Niech
jest wymierna. Niech
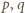 oznaczają takie względnie
pierwsze liczby naturalne, że
oznaczają takie względnie
pierwsze liczby naturalne, że
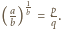 Wtedy
Wtedy
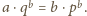 Wobec
tego, że
Wobec
tego, że
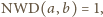 liczba
liczba
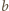 jest dzielnikiem liczby
jest dzielnikiem liczby
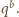 Również liczba
Również liczba
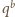 jest dzielnikiem
jest dzielnikiem
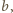 bo
bo
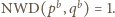 Stąd wynika, że
Stąd wynika, że
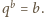 Nie jest to
możliwe, bo
Nie jest to
możliwe, bo
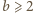 (liczba
(liczba
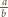 nie jest całkowita!), zatem
nie jest całkowita!), zatem
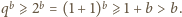
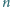 będzie liczbą całkowitą dodatnią. Udowodnić, że liczba
będzie liczbą całkowitą dodatnią. Udowodnić, że liczba
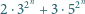
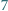 wtedy i tylko wtedy, gdy
wtedy i tylko wtedy, gdy
 jest liczbą
parzystą.
jest liczbą
parzystą.
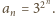 Zauważmy, że
Zauważmy, że
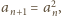 więc skoro
więc skoro
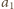 daje resztę
daje resztę
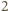 z dzielenia przez
z dzielenia przez
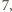 to
to
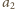 daje resztę
daje resztę
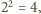
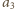 – tę samą resztę co
– tę samą resztę co
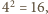 czyli znowu
czyli znowu
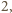 itd. Podobnie, jeśli
itd. Podobnie, jeśli
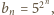 to
to
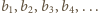 dają
odpowiednio reszty
dają
odpowiednio reszty
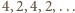 z dzielenia przez
z dzielenia przez
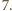 Zatem nasza
liczba
Zatem nasza
liczba
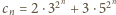 dla
dla
 nieparzystego daje tę samą resztę
przy dzieleniu przez
nieparzystego daje tę samą resztę
przy dzieleniu przez
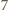 co
co
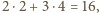 czyli
czyli
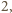 a dla
a dla
 parzystego tę samą resztę co liczba
parzystego tę samą resztę co liczba
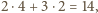 czyli
czyli
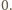
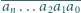 oznacza liczbę, której cyfrą jedności w zapisie
dziesiętnym jest
oznacza liczbę, której cyfrą jedności w zapisie
dziesiętnym jest
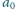 , cyfrą dziesiątek –
, cyfrą dziesiątek –
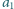 , cyfrą setek –
, cyfrą setek –
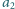 ,
itd. Znaleźć wszystkie liczby czterocyfrowe
,
itd. Znaleźć wszystkie liczby czterocyfrowe
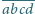 , które spełniają
równość
, które spełniają
równość

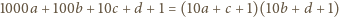
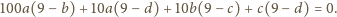
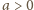 i wszystkie składniki lewej strony są nieujemne, to musi
być
i wszystkie składniki lewej strony są nieujemne, to musi
być
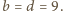
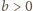 implikuje, że
implikuje, że
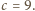 Otrzymujemy
więc liczby
Otrzymujemy
więc liczby
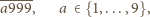
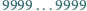 jest zapisana za pomocą
jest zapisana za pomocą
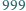 dziewiątek. Ile
wynosi suma cyfr kwadratu tej liczby?
dziewiątek. Ile
wynosi suma cyfr kwadratu tej liczby?
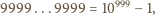
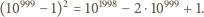
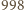 dziewiątek, a potem już prawie same zera
dziewiątek, a potem już prawie same zera
 Wychodzi
Wychodzi
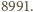
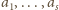 to będą liczby tych, którzy uścisnęli dłonie – odpowiednio –
to będą liczby tych, którzy uścisnęli dłonie – odpowiednio –
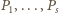 osobom, natomiast
osobom, natomiast
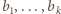 – liczby tych, którzy
uścisnęli dłonie
– liczby tych, którzy
uścisnęli dłonie
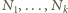 osobom, przy czym
osobom, przy czym
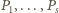 to liczby
parzyste,
to liczby
parzyste,
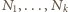 zaś – nieparzyste. Podwojona suma wszystkich
uścisków to
zaś – nieparzyste. Podwojona suma wszystkich
uścisków to
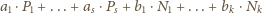
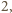 więc
więc
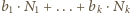 też
jest podzielna przez
też
jest podzielna przez
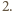 Interesuje nas suma
Interesuje nas suma
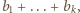 która
również jest liczbą parzystą, bo parzystość liczby
która
również jest liczbą parzystą, bo parzystość liczby
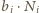 jest dla
każdego
jest dla
każdego
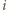 taka sama, jak parzystość
taka sama, jak parzystość
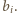
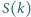 oznacza sumę cyfr liczby całkowitej
oznacza sumę cyfr liczby całkowitej
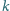 w zapisie
dziesiętnym. Dowieść, że istnieje nieskończenie wiele takich dodatnich liczb
całkowitych
w zapisie
dziesiętnym. Dowieść, że istnieje nieskończenie wiele takich dodatnich liczb
całkowitych
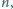 że
że

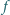 o współczynnikach całkowitych, dla którego
istnieją takie parami różne liczby całkowite
o współczynnikach całkowitych, dla którego
istnieją takie parami różne liczby całkowite
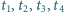 , że
, że

 , dla której
, dla której
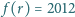 .
.
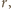 dla
której
dla
której
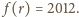 Korzystając z tego, że
Korzystając z tego, że
 dzieli
dzieli
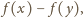 dla dowolnych liczb całkowitych
dla dowolnych liczb całkowitych
 i
i
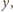 mamy
mamy

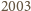 jest pierwsza, więc skoro liczby
jest pierwsza, więc skoro liczby
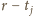 są parami różne,
to bez straty ogólności możemy przyjąć, że
są parami różne,
to bez straty ogólności możemy przyjąć, że

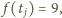 więc po podzieleniu z resztą wielomianu
więc po podzieleniu z resztą wielomianu
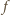 przez wielomian
przez wielomian
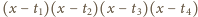 mamy
mamy
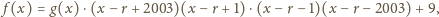
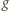 o współczynnikach całkowitych.
Podstawiając
o współczynnikach całkowitych.
Podstawiając
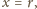 dostajemy
dostajemy
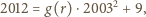
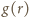 jest liczbą całkowitą.
jest liczbą całkowitą.
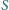 będzie skończonym zbiorem liczb całkowitych. Wykazać, że
istnieje wielomian stopnia pierwszego, o współczynnikach całkowitych,
którego wartości w punktach zbioru
będzie skończonym zbiorem liczb całkowitych. Wykazać, że
istnieje wielomian stopnia pierwszego, o współczynnikach całkowitych,
którego wartości w punktach zbioru
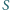 są parami względnie pierwsze.
są parami względnie pierwsze.
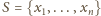 będzie zadanym zbiorem liczb całkowitych.
Określamy liczbę
będzie zadanym zbiorem liczb całkowitych.
Określamy liczbę
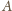 jako iloczyn wszystkich różnic
jako iloczyn wszystkich różnic
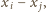 gdzie
gdzie
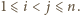 Pokażemy, że wielomian
Pokażemy, że wielomian
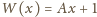 spełnia
wymagany warunek.
spełnia
wymagany warunek.
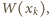
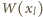 mają
wspólny dzielnik pierwszy
mają
wspólny dzielnik pierwszy
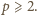 Liczba
Liczba
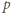 jest wówczas także
dzielnikiem różnicy
jest wówczas także
dzielnikiem różnicy
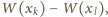 równej
równej
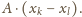 Skoro
Skoro
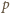 jest liczbą pierwszą, musi dzielić jeden z czynników:
jest liczbą pierwszą, musi dzielić jeden z czynników:
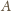 lub
lub
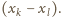 Ten drugi czynnik jest też dzielnikiem liczby
Ten drugi czynnik jest też dzielnikiem liczby
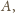 więc,
tak czy inaczej,
więc,
tak czy inaczej,
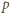 dzieli
dzieli
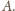 To już jest oczekiwana sprzeczność,
bo liczby
To już jest oczekiwana sprzeczność,
bo liczby
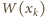 oraz
oraz
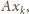 różniące się o 1, nie mogą być
jednocześnie podzielne przez
różniące się o 1, nie mogą być
jednocześnie podzielne przez
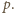
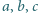 spełniające
spełniające
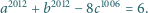
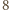 daje resztę
daje resztę
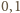 lub
lub
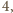 więc suma dwóch kwadratów – resztę
więc suma dwóch kwadratów – resztę
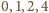 lub
lub
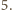 Gdyby istniały liczby całkowite
Gdyby istniały liczby całkowite
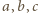 spełniające równanie
z treści zadania, to liczba
spełniające równanie
z treści zadania, to liczba
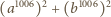
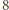 resztę
resztę
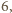 co jest niemożliwe.
co jest niemożliwe.
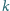 o następującej
własności:
o następującej
własności: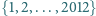 znajdą się dwie liczby, których suma lub różnica wynosi 671.
znajdą się dwie liczby, których suma lub różnica wynosi 671.
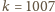 ma żądaną własność.
Podzielmy nasz zbiór
ma żądaną własność.
Podzielmy nasz zbiór
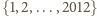 na dwuelementowe podzbiory
na dwuelementowe podzbiory
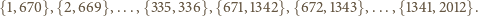
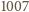 -elementowy podzbiór, to któreś dwa jego
elementy tworzą jeden z powyższych zbiorów (ich jest
-elementowy podzbiór, to któreś dwa jego
elementy tworzą jeden z powyższych zbiorów (ich jest
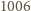 ). Zatem
suma lub różnica tych elementów wynosi
). Zatem
suma lub różnica tych elementów wynosi
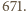
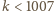 nie spełniają podanego
warunku. Wystarczy to zrobić dla
nie spełniają podanego
warunku. Wystarczy to zrobić dla
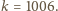 Rozważmy zbiór
Rozważmy zbiór
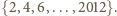 Sumy i różnice jego elementów są liczbami
parzystymi, żadna więc nie może wynosić
Sumy i różnice jego elementów są liczbami
parzystymi, żadna więc nie może wynosić
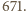
 , nie większą od
, nie większą od
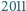 , dla
której liczba
, dla
której liczba
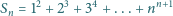
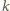 liczby
liczby
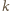 i
i
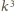 dają tę samą resztę z dzielenia przez 3 (wystarczy to sprawdzić dla
dają tę samą resztę z dzielenia przez 3 (wystarczy to sprawdzić dla
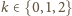 ). Zatem liczby
). Zatem liczby
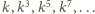 dają tę samą resztę
z dzielenia przez 3. Stąd
dają tę samą resztę
z dzielenia przez 3. Stąd
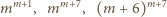
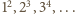 jest więc okresowy o okresie 6 i zaczyna się od
jest więc okresowy o okresie 6 i zaczyna się od
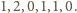 Ponieważ
Ponieważ
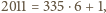 więc
więc
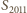 daje
przy dzieleniu przez 3 tę samą resztę co
daje
przy dzieleniu przez 3 tę samą resztę co
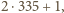 czyli 2. Stąd
czyli 2. Stąd
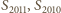 nie są podzielne przez 3, zaś
nie są podzielne przez 3, zaś
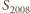 już jest.
już jest.
 liczba
liczba
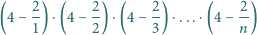
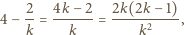
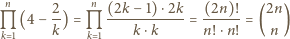
 będzie liczbą naturalną większą od 2. Dowieść, że ze zbioru
będzie liczbą naturalną większą od 2. Dowieść, że ze zbioru
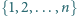 można usunąć dwie liczby tak, by suma liczb, które
pozostały, była kwadratem liczby naturalnej.
można usunąć dwie liczby tak, by suma liczb, które
pozostały, była kwadratem liczby naturalnej.
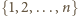 wynosi
wynosi
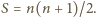 Suma dwóch liczb z tego zbioru może być
dowolną liczbą naturalną od 3 do
Suma dwóch liczb z tego zbioru może być
dowolną liczbą naturalną od 3 do
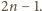 Usuwamy dwie –
suma liczb, które pozostały, może być dowolną liczbą naturalną od
Usuwamy dwie –
suma liczb, które pozostały, może być dowolną liczbą naturalną od
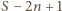 do
do
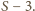 Wystarczy wykazać, że w przedziale
Wystarczy wykazać, że w przedziale
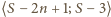 znajduje się jakiś kwadrat liczby naturalnej.
znajduje się jakiś kwadrat liczby naturalnej.
 będzie największą liczbą naturalną, której kwadrat
nie przekracza
będzie największą liczbą naturalną, której kwadrat
nie przekracza
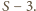 Wówczas
Wówczas
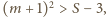 skąd
skąd
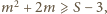 czyli
czyli
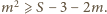 Wystarczy wykazać, że
prawa strona ostatniej nierówności jest nie mniejsza niż
Wystarczy wykazać, że
prawa strona ostatniej nierówności jest nie mniejsza niż
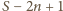 ; czyli
że zachodzi nierówność
; czyli
że zachodzi nierówność
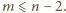 Dla
Dla
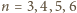 różnica
różnica
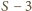 wynosi kolejno
wynosi kolejno
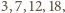 co daje wartości
co daje wartości
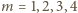 ;
mamy równość
;
mamy równość
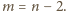 Dla
Dla
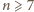 szacujemy kwadrat liczby
szacujemy kwadrat liczby
 :
:
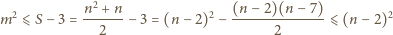
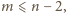 którą chcieliśmy wykazać.
którą chcieliśmy wykazać.
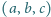 będzie trójką liczb całkowitych dodatnich spełniających
równanie
będzie trójką liczb całkowitych dodatnich spełniających
równanie
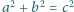 . Udowodnić, że nie istnieje liczba naturalna
. Udowodnić, że nie istnieje liczba naturalna
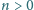 , dla której liczba
, dla której liczba
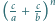 byłaby całkowita.
byłaby całkowita.
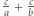 jest całkowita wtedy i tylko wtedy, gdy liczba
jest całkowita wtedy i tylko wtedy, gdy liczba
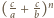 jest całkowita. Wystarczy zatem rozważyć przypadek
jest całkowita. Wystarczy zatem rozważyć przypadek
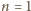 . Załóżmy nie wprost, że
. Załóżmy nie wprost, że
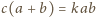 dla pewnej
liczby całkowitej
dla pewnej
liczby całkowitej
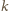 . Wiemy, że
. Wiemy, że
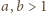 . Możemy założyć
bez utraty ogólności, że
. Możemy założyć
bez utraty ogólności, że
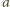 i
i
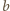 są względnie pierwsze
(jeśli nie są, to ich wspólny dzielnik dzieli też
są względnie pierwsze
(jeśli nie są, to ich wspólny dzielnik dzieli też
 i możemy
podzielić przez niego wszystkie trzy dane liczby). Wówczas
i możemy
podzielić przez niego wszystkie trzy dane liczby). Wówczas
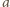 i
i
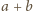 też są względnie pierwsze. Zatem, skoro
też są względnie pierwsze. Zatem, skoro
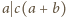 ,
to
,
to
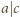 . Ale wtedy
. Ale wtedy
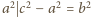 , więc
, więc
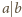 , co daje
sprzeczność.
, co daje
sprzeczność.
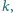 że liczba
że liczba
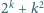 jest
pierwsza.
jest
pierwsza.
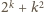 jest pierwsza. Jest ona większa od 2, więc
nieparzysta. Zatem liczba
jest pierwsza. Jest ona większa od 2, więc
nieparzysta. Zatem liczba
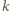 musi być nieparzysta. Ale wówczas
musi być nieparzysta. Ale wówczas
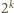 daje resztę
daje resztę
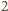 z dzielenia przez
z dzielenia przez
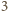 . Skoro kwadrat liczby
całkowitej daje resztę
. Skoro kwadrat liczby
całkowitej daje resztę
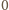 lub
lub
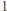 przy dzieleniu przez
przy dzieleniu przez
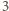 , to aby
, to aby
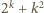 nie było podzielne przez
nie było podzielne przez
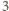 , potrzeba, aby
, potrzeba, aby
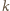 było
podzielne przez
było
podzielne przez
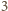 . Ponieważ
. Ponieważ
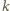 jest liczbą pierwszą, jedyna
możliwość to
jest liczbą pierwszą, jedyna
możliwość to
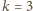 i wówczas
i wówczas
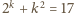 jest liczbą
pierwszą.
jest liczbą
pierwszą.
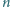 istnieje taka
liczba całkowita dodatnia
istnieje taka
liczba całkowita dodatnia
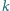 , że
, że
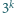 w zapisie dziesiętnym kończy
się cyframi
w zapisie dziesiętnym kończy
się cyframi
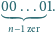
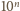 liczb
liczb
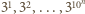 . Żadna z nich nie dzieli się
przez
. Żadna z nich nie dzieli się
przez
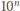 , więc możliwe reszty z dzielenia tych liczb przez
, więc możliwe reszty z dzielenia tych liczb przez
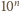 to
to
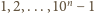 . Jest ich o jeden mniej niż liczb, więc istnieją dwie liczby,
powiedzmy
. Jest ich o jeden mniej niż liczb, więc istnieją dwie liczby,
powiedzmy
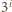 i
i
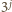 , dla
, dla
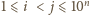 , które dają tę
samą resztę z dzielenia przez
, które dają tę
samą resztę z dzielenia przez
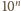 . Oznacza to, że
. Oznacza to, że
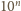 dzieli
dzieli
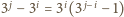 . Ale
. Ale
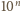 i
i
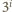 są względnie pierwsze, więc
są względnie pierwsze, więc
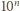 dzieli
dzieli
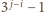 . Zatem
. Zatem
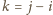 spełnia warunki
zadania.
spełnia warunki
zadania.
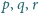 takie, że liczba
takie, że liczba

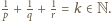 Pomnóżmy obie strony
równania przez
Pomnóżmy obie strony
równania przez
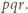 Wtedy
Wtedy
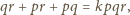
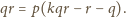
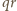 dzieli się przez
dzieli się przez
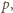 sprzeczność. Zatem liczby
sprzeczność. Zatem liczby
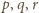 o żądanych własnościach nie istnieją.
o żądanych własnościach nie istnieją.
 zapisano jako
zapisano jako
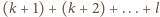 dla
pewnych liczb naturalnych
dla
pewnych liczb naturalnych
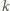 i
i
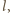 takich że
takich że
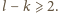 To
oznacza, że
To
oznacza, że
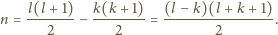
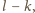
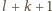 jest nieparzysta
i większa od
jest nieparzysta
i większa od
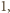 czyli
czyli
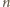 ma czynnik nieparzysty, więc nie jest potęgą
dwójki. Z drugiej strony, jeżeli
ma czynnik nieparzysty, więc nie jest potęgą
dwójki. Z drugiej strony, jeżeli
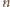 nie jest potęgą dwójki, to
liczba
nie jest potęgą dwójki, to
liczba
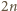 zapisuje się jako iloczyn liczby parzystej i nieparzystej
zapisuje się jako iloczyn liczby parzystej i nieparzystej
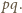 Jeśli
Jeśli
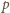 oznacza większą z tych liczb, to możemy przyjąć,
iż
oznacza większą z tych liczb, to możemy przyjąć,
iż
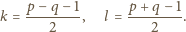
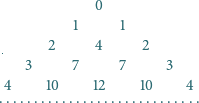
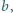
 są sąsiednimi elementami
dowolnego wiersza, nad nimi znajduje się liczba
są sąsiednimi elementami
dowolnego wiersza, nad nimi znajduje się liczba
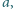 zaś pod nimi liczba
zaś pod nimi liczba
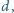 to
to
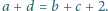 Udowodnić, że dla każdej liczby
całkowitej
Udowodnić, że dla każdej liczby
całkowitej
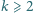 istnieje nieskończenie wiele liczb, z których każda
występuje w tej tabeli dokładnie
istnieje nieskończenie wiele liczb, z których każda
występuje w tej tabeli dokładnie
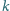 razy.
razy.
 tak, by otrzymać tabelę – nieskończoną
macierz
tak, by otrzymać tabelę – nieskończoną
macierz
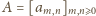 ; jest to lewa z dwóch tabelek poniżej:
; jest to lewa z dwóch tabelek poniżej:

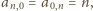
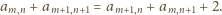
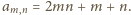 Sprawdzamy, że te liczby spełniają
napisane przed chwilą równania (które wyznaczają zawartość całej tabeli
jednoznacznie).
Sprawdzamy, że te liczby spełniają
napisane przed chwilą równania (które wyznaczają zawartość całej tabeli
jednoznacznie).
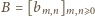 o wyrazach
o wyrazach
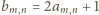 (prawy diagram powyżej). Zachodzą równości
(prawy diagram powyżej). Zachodzą równości
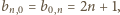
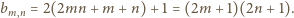
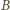 jest po prostu tabliczką mnożenia liczb nieparzystych. Każda
liczba nieparzysta występuje w niej tyle razy, ile ma różnych dzielników
dodatnich.
jest po prostu tabliczką mnożenia liczb nieparzystych. Każda
liczba nieparzysta występuje w niej tyle razy, ile ma różnych dzielników
dodatnich.
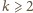 będzie zadaną liczbą całkowitą. Bierzemy dowolną
liczbę pierwszą
będzie zadaną liczbą całkowitą. Bierzemy dowolną
liczbę pierwszą
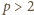 ; wówczas liczba
; wówczas liczba
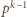 wystąpi w tabeli
wystąpi w tabeli
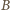 dokładnie
dokładnie
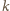 razy. Wracając do tabeli
razy. Wracając do tabeli
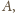 widzimy, że
dokładnie
widzimy, że
dokładnie
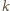 razy pojawi się w niej liczba
razy pojawi się w niej liczba
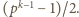 Jest
nieskończenie wiele liczb pierwszych – mamy więc tezę zadania.
Jest
nieskończenie wiele liczb pierwszych – mamy więc tezę zadania.