Klub 44M - zadania II 2020»Zadanie 796
o zadaniu...
- Zadanie pochodzi z artykułu Klub 44M - zadania II 2020
- Publikacja w Delcie: luty 2020
- Publikacja elektroniczna: 1 lutego 2020
- Artykuł źródłowy w wersji do druku [application/pdf]: (496 KB)
-
Zadanie 796 zaproponował pan Witold Bednarek z Łodzi.
Dane są liczby całkowite 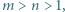 przy czym
przy czym 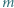 jest liczbą parzystą. Udowodnić, że równanie
jest liczbą parzystą. Udowodnić, że równanie
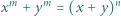 |
ma rozwiązanie w liczbach całkowitych dodatnich 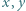 wtedy i tylko wtedy, gdy
wtedy i tylko wtedy, gdy 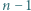 dzieli się przez
dzieli się przez 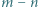 .
.

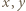 spełniają podane równanie. Oznaczmy przez
spełniają podane równanie. Oznaczmy przez 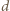 ich największy wspólny dzielnik; tak więc
ich największy wspólny dzielnik; tak więc 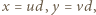 gdzie
gdzie 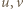 to liczby naturalne względnie pierwsze. Wstawiając to do równania i dzieląc stronami przez
to liczby naturalne względnie pierwsze. Wstawiając to do równania i dzieląc stronami przez 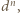 otrzymujemy
otrzymujemy
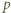 będzie dowolnym dzielnikiem pierwszym liczby
będzie dowolnym dzielnikiem pierwszym liczby 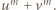 Wobec związku (1)
Wobec związku (1) 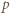 jest też dzielnikiem sumy
jest też dzielnikiem sumy 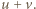 To znaczy, że
To znaczy, że 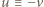 (mod
(mod 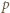 ); a skoro
); a skoro 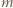 jest liczbą parzystą, mamy stąd
jest liczbą parzystą, mamy stąd 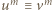 (mod
(mod 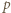 ), i dalej
), i dalej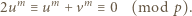
 nie dzieli się przez
nie dzieli się przez 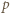 (bo
(bo 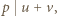 zaś
zaś 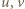 są względnie pierwsze); zatem
są względnie pierwsze); zatem 
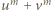 nie ma innych dzielników pierwszych, znaczy to, że
nie ma innych dzielników pierwszych, znaczy to, że
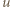 i
i  (względnie pierwsze) są obie nieparzyste; stąd
(względnie pierwsze) są obie nieparzyste; stąd 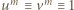 (mod 4), bo
(mod 4), bo 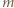 jest liczbą parzystą. W równości (2) mamy więc
jest liczbą parzystą. W równości (2) mamy więc 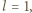 skąd
skąd 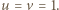 Wracamy do równania (1):
Wracamy do równania (1): 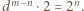 To pokazuje, że
To pokazuje, że 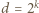 (dla pewnego
(dla pewnego 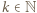 ); przy tym
); przy tym 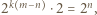 czyli
czyli 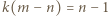 : liczba
: liczba 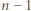 dzieli się przez
dzieli się przez 
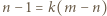 dla pewnego
dla pewnego 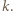 Wówczas para
Wówczas para 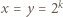 jest rozwiązaniem zadanego równania:
jest rozwiązaniem zadanego równania: