(a) Przypuśćmy, że liczby  oraz
oraz 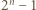 mają wspólny dzielnik pierwszy
mają wspólny dzielnik pierwszy 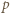 (jasne, że
(jasne, że 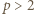 ). Wykażemy, że wówczas liczba
). Wykażemy, że wówczas liczba 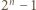 dzieli się przez
dzieli się przez 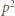 (nie jest więc bezkwadratowa). Zgodnie z małym twierdzeniem Fermata,
(nie jest więc bezkwadratowa). Zgodnie z małym twierdzeniem Fermata, 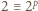 (mod
(mod 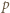 ). Podnosimy tę kongruencję stronami do potęgi
). Podnosimy tę kongruencję stronami do potęgi 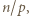 otrzymując
otrzymując 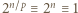 (mod
(mod 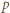 ). Zatem
). Zatem 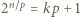 dla pewnej liczby całkowitej
dla pewnej liczby całkowitej 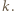 Stąd
Stąd
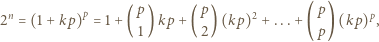
czyli 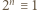 (mod
(mod 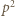 ); a to była nasza teza.
); a to była nasza teza.
(b) Przykład pokazujący, że nie zachodzi implikacja odwrotna, nie tak łatwo znaleźć (mała szansa, że trafimy, zwyczajnie próbując - bez komputera ciężko). Prosty program, który dla zadanej liczby pierwszej 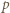 kontroluje dwie końcowe cyfry rozwinięcia (przy podstawie
kontroluje dwie końcowe cyfry rozwinięcia (przy podstawie 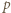 ) kolejnych potęg dwójki, pozwala znaleźć moment powtórzenia końcówki
) kolejnych potęg dwójki, pozwala znaleźć moment powtórzenia końcówki 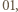 czyli wykładnik
czyli wykładnik 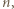 dla którego
dla którego 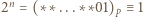 (mod
(mod 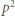 ). Powtarzamy tę procedurę dla kolejnych liczb pierwszych
). Powtarzamy tę procedurę dla kolejnych liczb pierwszych 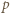 ; warto przy tym, dla oszczędności czasu, ograniczyć zakres wykładnika, np. do
; warto przy tym, dla oszczędności czasu, ograniczyć zakres wykładnika, np. do 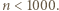 W ten sposób szybko znajdujemy parę
W ten sposób szybko znajdujemy parę 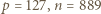 ; nie jest ona jednak szukanym kontrprzykładem, bowiem dla tej pary zachodzą związki
; nie jest ona jednak szukanym kontrprzykładem, bowiem dla tej pary zachodzą związki 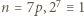 (mod
(mod 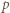 ), z których nietrudno wynika, że liczby
), z których nietrudno wynika, że liczby  i
i 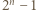 nie są względnie pierwsze.
nie są względnie pierwsze.
Następna znaleziona para 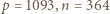 jest już dobra: gdyby liczby
jest już dobra: gdyby liczby 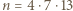 oraz
oraz  nie były względnie pierwsze, ta ostatnia musiałaby się dzielić przez 7 lub 13; ale minimalne wykładniki
nie były względnie pierwsze, ta ostatnia musiałaby się dzielić przez 7 lub 13; ale minimalne wykładniki 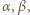 dla których
dla których 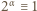 (mod 7),
(mod 7), 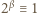 (mod 13), to
(mod 13), to 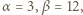 więc wykładnik
więc wykładnik 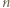 musiałby się dzielić przez 3; a tak nie jest. Skoro zaś ta para została wygenerowana przez algorytm, zapewniający podzielność
musiałby się dzielić przez 3; a tak nie jest. Skoro zaś ta para została wygenerowana przez algorytm, zapewniający podzielność 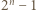 przez
przez 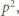 zatem liczba
zatem liczba 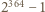 nie jest bezkwadratowa.
nie jest bezkwadratowa.
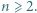
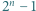 jest bezkwadratowa, to liczby
jest bezkwadratowa, to liczby 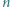 oraz
oraz 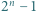 są względnie pierwsze.
są względnie pierwsze.
 oraz
oraz 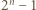 mają wspólny dzielnik pierwszy
mają wspólny dzielnik pierwszy 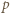 (jasne, że
(jasne, że 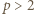 ). Wykażemy, że wówczas liczba
). Wykażemy, że wówczas liczba 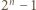 dzieli się przez
dzieli się przez 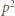 (nie jest więc bezkwadratowa). Zgodnie z małym twierdzeniem Fermata,
(nie jest więc bezkwadratowa). Zgodnie z małym twierdzeniem Fermata, 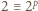 (mod
(mod 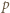 ). Podnosimy tę kongruencję stronami do potęgi
). Podnosimy tę kongruencję stronami do potęgi 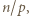 otrzymując
otrzymując 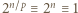 (mod
(mod 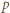 ). Zatem
). Zatem 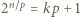 dla pewnej liczby całkowitej
dla pewnej liczby całkowitej 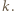 Stąd
Stąd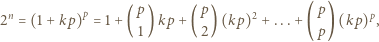
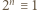 (mod
(mod 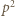 ); a to była nasza teza.
); a to była nasza teza.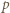 kontroluje dwie końcowe cyfry rozwinięcia (przy podstawie
kontroluje dwie końcowe cyfry rozwinięcia (przy podstawie 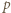 ) kolejnych potęg dwójki, pozwala znaleźć moment powtórzenia końcówki
) kolejnych potęg dwójki, pozwala znaleźć moment powtórzenia końcówki 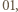 czyli wykładnik
czyli wykładnik 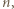 dla którego
dla którego 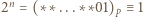 (mod
(mod 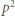 ). Powtarzamy tę procedurę dla kolejnych liczb pierwszych
). Powtarzamy tę procedurę dla kolejnych liczb pierwszych 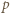 ; warto przy tym, dla oszczędności czasu, ograniczyć zakres wykładnika, np. do
; warto przy tym, dla oszczędności czasu, ograniczyć zakres wykładnika, np. do 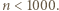 W ten sposób szybko znajdujemy parę
W ten sposób szybko znajdujemy parę 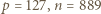 ; nie jest ona jednak szukanym kontrprzykładem, bowiem dla tej pary zachodzą związki
; nie jest ona jednak szukanym kontrprzykładem, bowiem dla tej pary zachodzą związki 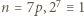 (mod
(mod 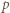 ), z których nietrudno wynika, że liczby
), z których nietrudno wynika, że liczby  i
i 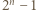 nie są względnie pierwsze.
nie są względnie pierwsze.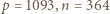 jest już dobra: gdyby liczby
jest już dobra: gdyby liczby 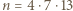 oraz
oraz  nie były względnie pierwsze, ta ostatnia musiałaby się dzielić przez 7 lub 13; ale minimalne wykładniki
nie były względnie pierwsze, ta ostatnia musiałaby się dzielić przez 7 lub 13; ale minimalne wykładniki 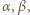 dla których
dla których 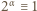 (mod 7),
(mod 7), 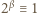 (mod 13), to
(mod 13), to 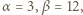 więc wykładnik
więc wykładnik 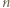 musiałby się dzielić przez 3; a tak nie jest. Skoro zaś ta para została wygenerowana przez algorytm, zapewniający podzielność
musiałby się dzielić przez 3; a tak nie jest. Skoro zaś ta para została wygenerowana przez algorytm, zapewniający podzielność 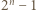 przez
przez 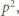 zatem liczba
zatem liczba 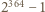 nie jest bezkwadratowa.
nie jest bezkwadratowa.