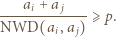Zadanie ZM-1592
o zadaniu...
- Publikacja w Delcie: luty 2019
- Publikacja elektroniczna: 1 lutego 2019
Nana jest dodatnia liczba całkowita 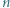 o tej własności, że
o tej własności, że 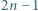 jest liczbą pierwszą. Wykazać, że w zbiorze dowolnych
jest liczbą pierwszą. Wykazać, że w zbiorze dowolnych 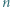 różnych dodatnich liczb całkowitych można wskazać takie dwie liczby
różnych dodatnich liczb całkowitych można wskazać takie dwie liczby 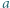 i
i 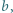 że
że


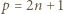 i rozważmy dowolne liczby całkowite
i rozważmy dowolne liczby całkowite 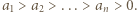 Zauważmy, że jeśli te liczby mają wspólny dzielnik większy od
Zauważmy, że jeśli te liczby mają wspólny dzielnik większy od 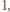 to możemy każdą z nich przezeń podzielić, zachowując postać tezy zadania. Wobec tego możemy bez straty ogólności założyć, że
to możemy każdą z nich przezeń podzielić, zachowując postać tezy zadania. Wobec tego możemy bez straty ogólności założyć, że 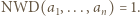
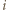 o tej własności, że
o tej własności, że 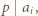 to dla pewnego
to dla pewnego 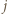 mamy
mamy 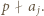 Wówczas
Wówczas 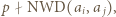 więc
więc
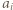 nie jest podzielna przez
nie jest podzielna przez 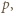 to reszty z dzielenia przez
to reszty z dzielenia przez 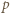 pewnych dwóch z nich należą do tego samego spośród
pewnych dwóch z nich należą do tego samego spośród 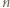 zbiorów
zbiorów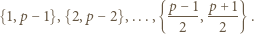
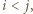 że
że 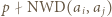 oraz
oraz 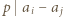 lub
lub 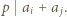 W pierwszym przypadku mamy
W pierwszym przypadku mamy