Zadanie ZM-1569
o zadaniu...
- Publikacja w Delcie: czerwiec 2018
- Publikacja elektroniczna: 22 maja 2018
Wykazać, że istnieje nieskończenie wiele dodatnich liczb całkowitych, których nie można zapisać w postaci sumy dwóch elementów zbioru 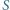 oraz nieskończenie wiele dodatnich liczb całkowitych, które można zapisać w takiej postaci.
oraz nieskończenie wiele dodatnich liczb całkowitych, które można zapisać w takiej postaci.

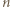 jest liczbą podzielną przez
jest liczbą podzielną przez 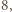 to
to  nie można zapisać w postaci sumy dwóch elementów zbioru
nie można zapisać w postaci sumy dwóch elementów zbioru 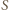 albo - w myśl tezy poprzedniego zadania - w postaci iloczynu dwóch elementów zbioru
albo - w myśl tezy poprzedniego zadania - w postaci iloczynu dwóch elementów zbioru 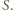 Przypuśćmy, że
Przypuśćmy, że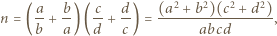
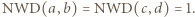 Skoro
Skoro 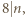 to co najmniej jeden z czynników w liczniku powyższego ułamka jest podzielny przez
to co najmniej jeden z czynników w liczniku powyższego ułamka jest podzielny przez 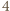 ; bez straty ogólności załóżmy, że
; bez straty ogólności załóżmy, że 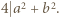 Stąd wynika, że liczby
Stąd wynika, że liczby 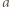 i
i 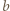 są tej samej parzystości, skąd wobec
są tej samej parzystości, skąd wobec 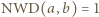 - obie są nieparzyste. Jednak wówczas
- obie są nieparzyste. Jednak wówczas 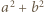 daje resztę
daje resztę 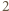 przy dzieleniu przez
przy dzieleniu przez 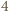 - sprzeczność.
- sprzeczność.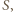 rozważymy ciąg Fibonacciego
rozważymy ciąg Fibonacciego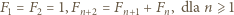
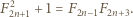
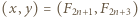 mamy więc
mamy więc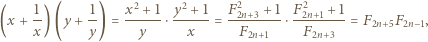
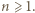 To kończy dowód, gdyż dla różnych
To kończy dowód, gdyż dla różnych 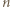 otrzymujemy różne liczby.
otrzymujemy różne liczby.