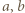Niech będą liczbami naturalnymi, spełniającymi warunek 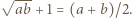Wymierny pierwiastek z liczby naturalnej jest liczbą naturalną. Zatem 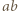musi być kwadratem liczby naturalnej. Oznaczając przez 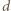największy wspólny dzielnik liczb 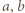(tak, że 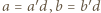; 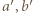względnie pierwsze) widzimy, że czynniki 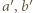muszą być kwadratami: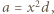 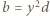( 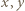naturalne). Badane równanie przybiera postać 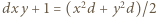; po przekształceniu: 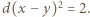Stąd wniosek, że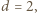

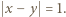
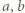Uzyskaliśmy odpowiedź: liczby to podwojone kwadraty dwóch kolejnych liczb naturalnych. Proste sprawdzenie pokazuje, że każda taka para spełnia wymagany warunek.