Nie tracimy ogólności, rozważając jedynie niemalejące ciągi 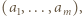 dzięki czemu wyrazy sumy
dzięki czemu wyrazy sumy
 |
(1) |
są uporządkowane nierosnąco. Niech 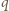 oraz
oraz  oznaczają iloraz i resztę z dzielenia
oznaczają iloraz i resztę z dzielenia 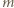 przez
przez 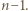 Wykażemy, że ciąg
Wykażemy, że ciąg
 |
(2) |
jest tym, dla którego suma (1) - pozostając mniejszą od 1 - jest maksymalna. Wynosi ona
 |
(3) |
Niech więc 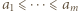 będzie dowolnym ciągiem, dla którego wartość sumy (1) jest mniejsza od 1. Przypuśćmy, że pewien wyraz
będzie dowolnym ciągiem, dla którego wartość sumy (1) jest mniejsza od 1. Przypuśćmy, że pewien wyraz 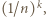 z wykładnikiem
z wykładnikiem 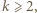 powtarza się co najmniej
powtarza się co najmniej 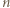 razy. Przyjmijmy, że
razy. Przyjmijmy, że 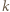 jest największym takim numerem. Wykreślamy
jest największym takim numerem. Wykreślamy 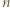 składników równych
składników równych 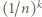 i zastępujemy je pojedynczym wyrazem
i zastępujemy je pojedynczym wyrazem 
Wartość sumy nie uległa zmianie, ale ciąg skrócił się o 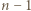 wyrazów. Dopisujemy więc na końcu
wyrazów. Dopisujemy więc na końcu 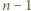 ułamków, z wykładnikami tak dużymi, by wartość sumy (1) (która się powiększa!) pozostała mniejsza od 1 - bacząc jedynie, by żaden wyraz (z wykładnikiem
ułamków, z wykładnikami tak dużymi, by wartość sumy (1) (która się powiększa!) pozostała mniejsza od 1 - bacząc jedynie, by żaden wyraz (z wykładnikiem 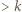 ) nie powtórzył się
) nie powtórzył się 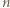 -krotnie.
-krotnie.
Powtarzamy tę modyfikację tak długo, dopóki istnieje blok jednakowych składników 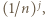 długości co najmniej
długości co najmniej 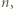 z jakimkolwiek wykładnikiem
z jakimkolwiek wykładnikiem 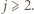 Mógłby ewentualnie pozostać taki blok dla wykładnika
Mógłby ewentualnie pozostać taki blok dla wykładnika 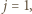 czyli złożony ze składników równych
czyli złożony ze składników równych 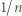 - ale to też nie jest możliwe, skoro przez cały czas była prowadzona kontrola, by suma nie osiągnęła wartości 1. Stąd wynika, że w dalszym ciągu dowodu można ograniczać uwagę do ciągów
- ale to też nie jest możliwe, skoro przez cały czas była prowadzona kontrola, by suma nie osiągnęła wartości 1. Stąd wynika, że w dalszym ciągu dowodu można ograniczać uwagę do ciągów 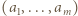 o własnościach:
o własnościach:
 |
(4) |
Ciąg (2) spełnia te warunki. Dla wykazania jego optymalności weźmy pod uwagę dowolny inny ciąg 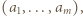 także spełniający powyższe warunki, i oznaczmy przez
także spełniający powyższe warunki, i oznaczmy przez 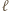 najwcześniejszy numer, dla którego
najwcześniejszy numer, dla którego 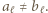 Zatem odcinki
Zatem odcinki 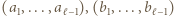 są identyczne.
są identyczne.
Nietrudno zauważyć, że 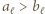 ; w przeciwnym przypadku mielibyśmy
; w przeciwnym przypadku mielibyśmy 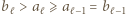 ; to by oznaczało, że
; to by oznaczało, że 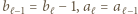 i że w ciągu (2)
i że w ciągu (2) 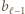 jest wyrazem kończącym blok złożony z
jest wyrazem kończącym blok złożony z 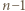 równych liczb. Skoro zaś
równych liczb. Skoro zaś 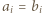 dla
dla 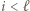 oraz
oraz 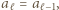 mielibyśmy w ciągu
mielibyśmy w ciągu 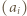 blok złożony z
blok złożony z  równych liczb, wbrew warunkowi (4). Tak więc
równych liczb, wbrew warunkowi (4). Tak więc 
Dokonujemy kolejnej modyfikacji ciągu 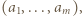 zastępując wyraz
zastępując wyraz 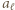 liczbą
liczbą 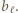 Warunki (4) pozostają spełnione, wartość sumy (1) zwiększa się, zaś nowy ciąg pokrywa się z ciągiem (2) na odcinku
Warunki (4) pozostają spełnione, wartość sumy (1) zwiększa się, zaś nowy ciąg pokrywa się z ciągiem (2) na odcinku 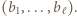 Po skończenie wielu takich krokach dochodzimy do ciągu
Po skończenie wielu takich krokach dochodzimy do ciągu 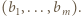 To pokazuje, że wartość sumy (1) dla wyjściowego ciągu
To pokazuje, że wartość sumy (1) dla wyjściowego ciągu 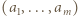 była mniejsza niż jej wartość dla ciągu
była mniejsza niż jej wartość dla ciągu 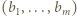 - czyli liczba dana wzorem (3), która wobec tego jest szukanym kresem górnym.
- czyli liczba dana wzorem (3), która wobec tego jest szukanym kresem górnym.
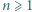 stosów monet, po jednej w każdym. W danej chwili możemy połączyć dwa dowolnie wybrane stosy w jeden. Jeśli połączymy stos
stosów monet, po jednej w każdym. W danej chwili możemy połączyć dwa dowolnie wybrane stosy w jeden. Jeśli połączymy stos 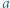 monet ze stosem
monet ze stosem 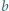 monet, to zapisujemy iloczyn
monet, to zapisujemy iloczyn 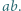 Te czynności wykonujemy aż do uzyskania jednego stosu
Te czynności wykonujemy aż do uzyskania jednego stosu 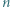 monet. Dowieść, że suma zapisanych iloczynów wynosi
monet. Dowieść, że suma zapisanych iloczynów wynosi 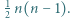
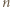 -kątów, w których
-kątów, w których 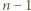 i
i 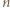 są przypisane sąsiednim wierzchołkom. Krok indukcji o głębokości
są przypisane sąsiednim wierzchołkom. Krok indukcji o głębokości 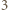 polega na dodaniu trzech wierzchołków z liczbami
polega na dodaniu trzech wierzchołków z liczbami 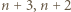 i
i 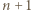 pomiędzy tymi dwoma.
pomiędzy tymi dwoma.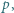 które można zapisać w postaci sumy
które można zapisać w postaci sumy 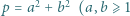 całkowite) tak, by liczba
całkowite) tak, by liczba 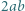 była kwadratem liczby całkowitej.
była kwadratem liczby całkowitej.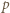 będzie liczbą pierwszą o rozważanej własności:
będzie liczbą pierwszą o rozważanej własności: 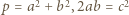 (
( 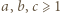 całkowite). Oznaczmy
całkowite). Oznaczmy 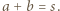 Tak więc
Tak więc 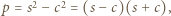 wobec czego
wobec czego 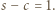 Równość
Równość 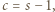 po podniesieniu stronami do kwadratu i podstawieniu wyrażeń określających
po podniesieniu stronami do kwadratu i podstawieniu wyrażeń określających 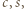 przybiera postać
przybiera postać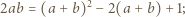
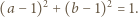
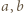 jest równa 2, a druga 1, i ostatecznie
jest równa 2, a druga 1, i ostatecznie 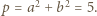 Skoro
Skoro 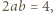 zatem liczba pierwsza
zatem liczba pierwsza 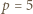 spełnia wymagane warunki, i jest to jedyna taka liczba.
spełnia wymagane warunki, i jest to jedyna taka liczba.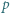 będzie nieparzystą liczbą pierwszą oraz
będzie nieparzystą liczbą pierwszą oraz 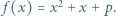 Przypuśćmy, że liczba
Przypuśćmy, że liczba 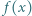 jest pierwsza dla każdej dodatniej liczby całkowitej
jest pierwsza dla każdej dodatniej liczby całkowitej  nie większej od
nie większej od 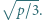 Wykazać, że liczba
Wykazać, że liczba 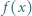 jest pierwsza dla każdej dodatniej liczby całkowitej
jest pierwsza dla każdej dodatniej liczby całkowitej 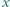 nie większej od
nie większej od 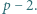
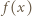 jest liczbą złożoną dla pewnego
jest liczbą złożoną dla pewnego 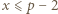 i oznaczmy przez
i oznaczmy przez  najmniejszą taką dodatnią liczbę całkowitą, że
najmniejszą taką dodatnią liczbę całkowitą, że 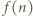 jest liczbą złożoną. Z założeń zadania wynika, że
jest liczbą złożoną. Z założeń zadania wynika, że 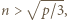 czyli
czyli 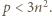
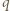 najmniejszy dzielnik pierwszy liczby
najmniejszy dzielnik pierwszy liczby 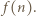 Zauważmy, że
Zauważmy, że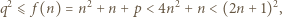
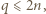 czyli istnieje liczba całkowita
czyli istnieje liczba całkowita 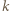 o tej własności, że
o tej własności, że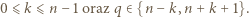
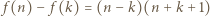
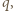 więc skoro
więc skoro 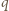 dzieli
dzieli 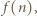 to również
to również 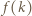 jest liczbą podzielną przez
jest liczbą podzielną przez 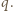 Pozostaje zauważyć, że
Pozostaje zauważyć, że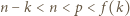
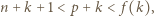
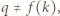 a co za tym idzie -
a co za tym idzie - 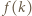 jest liczbą złożoną. Jednak
jest liczbą złożoną. Jednak 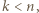 więc stoi to w sprzeczności z wyborem liczby
więc stoi to w sprzeczności z wyborem liczby 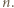
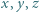 spełniające równanie
spełniające równanie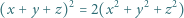
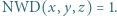
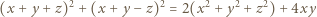

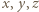 spełniają warunki zadania, to iloczyny
spełniają warunki zadania, to iloczyny 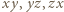 są nieujemne, co oznacza, że liczby
są nieujemne, co oznacza, że liczby 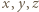 są wszystkie nieujemne lub wszystkie niedodatnie.
są wszystkie nieujemne lub wszystkie niedodatnie.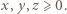 Ze związku (1) (oraz warunku, że
Ze związku (1) (oraz warunku, że 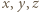 nie mają wspólnego dzielnika
nie mają wspólnego dzielnika 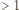 ) wynika, że
) wynika, że 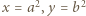 dla pewnej pary liczb całkowitych
dla pewnej pary liczb całkowitych 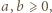 względnie pierwszych. Przepisujemy (1) jako
względnie pierwszych. Przepisujemy (1) jako 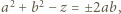 czyli
czyli 
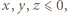 widzimy, że trójka
widzimy, że trójka 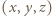 ma postać
ma postać
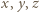 ma taką postać (więc
ma taką postać (więc 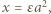
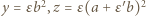 ;
; 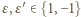 ), wówczas spełnione jest równanie (1) (równoważne wyjściowemu), zaś liczby
), wówczas spełnione jest równanie (1) (równoważne wyjściowemu), zaś liczby 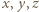 są względnie pierwsze. Wzór (2) przedstawia więc ogólne rozwiązanie postawionego zagadnienia.
są względnie pierwsze. Wzór (2) przedstawia więc ogólne rozwiązanie postawionego zagadnienia.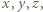 po ewentualnej jednoczesnej zmianie znaku, są kwadratami trzech względnie pierwszych liczb całkowitych, z których jedna jest sumą dwóch pozostałych
po ewentualnej jednoczesnej zmianie znaku, są kwadratami trzech względnie pierwszych liczb całkowitych, z których jedna jest sumą dwóch pozostałych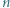 o tej własności, że
o tej własności, że 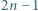 jest liczbą pierwszą. Wykazać, że w zbiorze dowolnych
jest liczbą pierwszą. Wykazać, że w zbiorze dowolnych 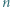 różnych dodatnich liczb całkowitych można wskazać takie dwie liczby
różnych dodatnich liczb całkowitych można wskazać takie dwie liczby 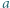 i
i 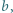 że
że
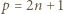 i rozważmy dowolne liczby całkowite
i rozważmy dowolne liczby całkowite 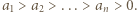 Zauważmy, że jeśli te liczby mają wspólny dzielnik większy od
Zauważmy, że jeśli te liczby mają wspólny dzielnik większy od 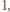 to możemy każdą z nich przezeń podzielić, zachowując postać tezy zadania. Wobec tego możemy bez straty ogólności założyć, że
to możemy każdą z nich przezeń podzielić, zachowując postać tezy zadania. Wobec tego możemy bez straty ogólności założyć, że 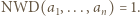
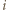 o tej własności, że
o tej własności, że 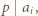 to dla pewnego
to dla pewnego 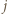 mamy
mamy 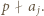 Wówczas
Wówczas 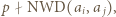 więc
więc
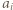 nie jest podzielna przez
nie jest podzielna przez 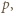 to reszty z dzielenia przez
to reszty z dzielenia przez 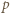 pewnych dwóch z nich należą do tego samego spośród
pewnych dwóch z nich należą do tego samego spośród 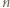 zbiorów
zbiorów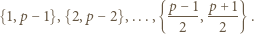
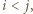 że
że 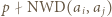 oraz
oraz 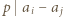 lub
lub 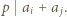 W pierwszym przypadku mamy
W pierwszym przypadku mamy
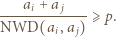
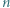 o tej własności, że
o tej własności, że 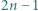 jest liczbą złożoną. Skonstruować zbiór
jest liczbą złożoną. Skonstruować zbiór 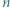 różnych dodatnich liczb całkowitych o tej własności, że dla każdych dwóch elementów tego zbioru
różnych dodatnich liczb całkowitych o tej własności, że dla każdych dwóch elementów tego zbioru 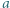 i
i 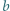 zachodzi nierówność
zachodzi nierówność
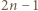 jest liczbą złożoną, to
jest liczbą złożoną, to 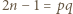 dla pewnych (niekoniecznie różnych) liczb nieparzystych
dla pewnych (niekoniecznie różnych) liczb nieparzystych 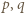 większych od
większych od 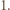 Niech
Niech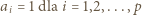
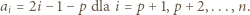
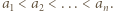
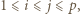 to
to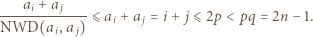
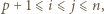 to
to 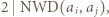 skąd
skąd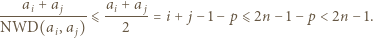
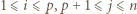 oraz
oraz 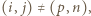 to
to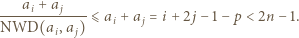
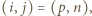 to
to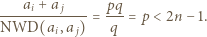
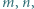 że nierówność
że nierówność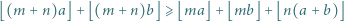
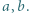
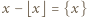 ; jest to liczba z przedziału
; jest to liczba z przedziału 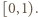 Znane (i łatwe do sprawdzenia) własności tego symbolu:
Znane (i łatwe do sprawdzenia) własności tego symbolu:

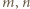 będą dodatnimi liczbami całkowitymi spełniającymi podany w zadaniu warunek. Dla
będą dodatnimi liczbami całkowitymi spełniającymi podany w zadaniu warunek. Dla 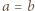 przybiera on postać
przybiera on postać
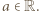 Podstawiamy
Podstawiamy 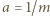 oraz
oraz 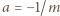 i otrzymujemy
i otrzymujemy
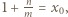 mamy więc
mamy więc
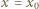 oraz dla
oraz dla 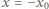 lewa strona (1) ma wartość niedodatnią. Zgodnie z własnością (1), ta wartość musi być zerem, co ma miejsce jedynie, gdy
lewa strona (1) ma wartość niedodatnią. Zgodnie z własnością (1), ta wartość musi być zerem, co ma miejsce jedynie, gdy 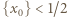 oraz
oraz 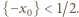 Dla tej liczby
Dla tej liczby 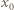 nie jest więc spełniona równość (2), co pokazuje, że
nie jest więc spełniona równość (2), co pokazuje, że 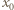 jest liczbą całkowitą, czyli że
jest liczbą całkowitą, czyli że  dzieli się przez
dzieli się przez 
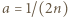 jej prawa strona jest dodatnia. Wobec tego i lewa strona musi być dodatnia, skąd
jej prawa strona jest dodatnia. Wobec tego i lewa strona musi być dodatnia, skąd 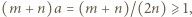 czyli
czyli 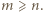 Ale
Ale  dzieli się przez
dzieli się przez  Zatem
Zatem 
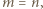 nierówność dana w zadaniu jest spełniona dla wszystkich liczb
nierówność dana w zadaniu jest spełniona dla wszystkich liczb 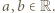 By to sprawdzić, oznaczmy
By to sprawdzić, oznaczmy 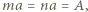
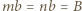 ; należy pokazać, że
; należy pokazać, że
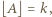
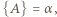
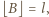
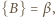 zależność (4) jest równoważna następującej:
zależność (4) jest równoważna następującej:

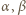 wynosi co najmniej
wynosi co najmniej 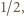 lewa strona (5) wynosi co najmniej 1 i nierówność (5) zachodzi; a jeśli
lewa strona (5) wynosi co najmniej 1 i nierówność (5) zachodzi; a jeśli 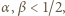 wówczas obie strony (5) są zerami.
wówczas obie strony (5) są zerami.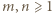 to pary równych liczb.
to pary równych liczb.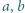 i
i 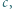 które spełniałyby równość
które spełniałyby równość 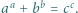
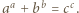 Bez straty ogólności
Bez straty ogólności 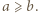 Można z tego wywnioskować nierówność
Można z tego wywnioskować nierówność 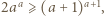 która prowadzi do sprzeczności.
która prowadzi do sprzeczności.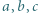 oraz
oraz 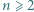 spełniają równość
spełniają równość 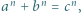 to
to 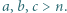
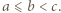 Należy uzasadnić i wykorzystać nierówność
Należy uzasadnić i wykorzystać nierówność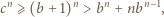
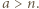
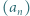 liczb naturalnych spełnia warunki
liczb naturalnych spełnia warunki 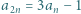 i
i 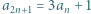 dla wszystkich naturalnych
dla wszystkich naturalnych 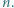 Dowieść, że jest to ciąg rosnący.
Dowieść, że jest to ciąg rosnący.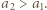 Załóżmy indukcyjnie, przy ustalonym
Załóżmy indukcyjnie, przy ustalonym 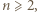 że
że 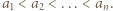 Trzeba dowieść, że
Trzeba dowieść, że 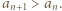 Należy tu rozważyć dwa przypadki:
Należy tu rozważyć dwa przypadki: 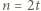 oraz
oraz 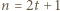 dla pewnego całkowitego dodatniego
dla pewnego całkowitego dodatniego 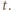 Pierwszy przypadek jest natychmiastowy i nie wymaga nawet skorzystania z założenia indukcyjnego. W drugim korzystamy z nierówności
Pierwszy przypadek jest natychmiastowy i nie wymaga nawet skorzystania z założenia indukcyjnego. W drugim korzystamy z nierówności 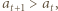 którą zapiszemy w postaci
którą zapiszemy w postaci 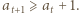
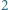 można przedstawić w postaci iloczynu trzech liczb naturalnych większych od
można przedstawić w postaci iloczynu trzech liczb naturalnych większych od 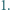
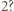
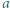 i
i 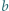 są naturalne. Dowieść, że istnieje taka liczba naturalna
są naturalne. Dowieść, że istnieje taka liczba naturalna 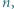 dla której
dla której 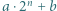 nie jest kwadratem liczby naturalnej.
nie jest kwadratem liczby naturalnej.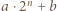 jest kwadratem dla każdego naturalnego
jest kwadratem dla każdego naturalnego 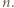 Wtedy liczby
Wtedy liczby 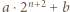 i
i 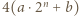 też są kwadratami, a różnica między nimi dla odpowiednio dużych
też są kwadratami, a różnica między nimi dla odpowiednio dużych  jest za mała.
jest za mała.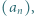 który spełnia warunki:
który spełnia warunki:

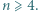
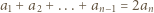
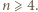 Z tego trzeba wywnioskować równość
Z tego trzeba wywnioskować równość 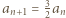 dla wszystkich
dla wszystkich 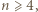 a to prowadzi do sprzeczności.
a to prowadzi do sprzeczności. zachodzi podzielność
zachodzi podzielność
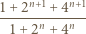
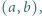 dla których liczby
dla których liczby 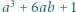 i
i 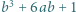 są sześcianami liczb naturalnych.
są sześcianami liczb naturalnych.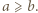 Wtedy
Wtedy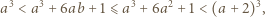
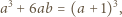
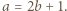 Podstawiając tę wartość, uzyskujemy oszacowania
Podstawiając tę wartość, uzyskujemy oszacowania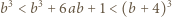
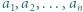 będą liczbami naturalnymi. Dowieść, że
będą liczbami naturalnymi. Dowieść, że
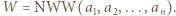 Liczby
Liczby 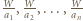 są naturalne i różne.
są naturalne i różne.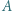 stanowi
stanowi 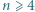 liczb naturalnych, przy czym spełniony jest warunek
liczb naturalnych, przy czym spełniony jest warunek 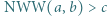 dla wszystkich parami różnych
dla wszystkich parami różnych 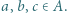 Dowieść, że suma odwrotności elementów zbioru
Dowieść, że suma odwrotności elementów zbioru 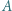 jest mniejsza od
jest mniejsza od 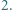
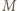 będzie największą liczbą w zbiorze
będzie największą liczbą w zbiorze 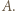 Każde
Każde 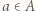 ma
ma 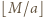 wielokrotności, które nie przekraczają
wielokrotności, które nie przekraczają 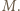 Z treści zadania wynika, że wszystkie te wielokrotności są różne.
Z treści zadania wynika, że wszystkie te wielokrotności są różne.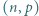 o tej własności, że
o tej własności, że 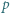 jest liczbą pierwszą większą od
jest liczbą pierwszą większą od 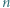 oraz
oraz 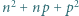 jest kwadratem liczby całkowitej.
jest kwadratem liczby całkowitej.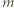 będzie taką dodatnią liczbą całkowitą, że
będzie taką dodatnią liczbą całkowitą, że 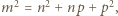 czyli
czyli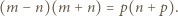
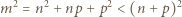
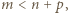 czyli
czyli 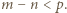 W szczególności liczba
W szczególności liczba 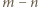 nie jest podzielna przez
nie jest podzielna przez 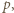 skąd wobec podzielności iloczynu
skąd wobec podzielności iloczynu 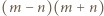 przez
przez 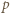 uzyskujemy
uzyskujemy 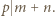 Ponadto skoro
Ponadto skoro 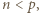 to
to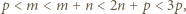
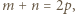 czyli
czyli 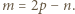 Zatem
Zatem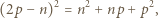
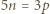 i wobec pierwszości liczby
i wobec pierwszości liczby 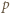 prowadzi do wniosku, że
prowadzi do wniosku, że 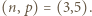 Jest to jedyna para o zadanych własnościach.
Jest to jedyna para o zadanych własnościach.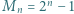 dla
dla 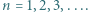 Udowodnić, że następujące dwa warunki są równoważne:
Udowodnić, że następujące dwa warunki są równoważne: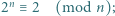
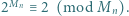
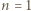 oba warunki są spełnione. Dalej przyjmujemy
oba warunki są spełnione. Dalej przyjmujemy 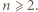 Zapiszmy liczbę
Zapiszmy liczbę 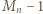 jako
jako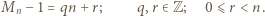
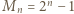 mamy kongruencję
mamy kongruencję 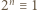 (mod
(mod 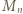 ), którą podnosimy do potęgi
), którą podnosimy do potęgi 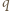 :
: 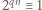 (mod
(mod 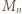 ); stąd po pomnożeniu przez
); stąd po pomnożeniu przez 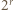 (i uwzględnieniu (1)):
(i uwzględnieniu (1)):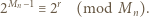
 jest dzielnikiem liczby
jest dzielnikiem liczby 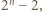 równej
równej 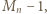 czyli w równości (1) jest
czyli w równości (1) jest 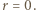 Ze związku (2) dostajemy
Ze związku (2) dostajemy 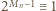 (mod
(mod 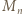 ); pomnożenie przez 2 daje warunek (ii).
); pomnożenie przez 2 daje warunek (ii).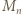 ) dzielimy stronami przez 2 (to dozwolone, bo
) dzielimy stronami przez 2 (to dozwolone, bo 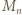 jest liczbą nieparzystą), otrzymując
jest liczbą nieparzystą), otrzymując 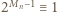 (mod
(mod 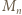 ). W połączeniu z (2) dostajemy
). W połączeniu z (2) dostajemy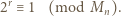
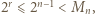 więc kongruencja (3) jest równością, skąd
więc kongruencja (3) jest równością, skąd 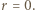 To znaczy, w myśl (1), że
To znaczy, w myśl (1), że  dzieli liczbę
dzieli liczbę 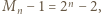 i mamy warunek (i).
i mamy warunek (i).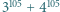 jest podzielna przez 13, 49, 181, 379, a nie jest podzielna przez 5 ani 11.
jest podzielna przez 13, 49, 181, 379, a nie jest podzielna przez 5 ani 11.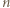 jest nieparzyste,
jest nieparzyste, 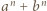 dzieli się przez
dzieli się przez 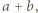 i wystarczy zauważyć, że
i wystarczy zauważyć, że 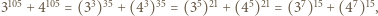 a więc
a więc 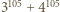 dzieli się przez
dzieli się przez 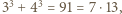 przez
przez 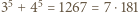 oraz przez
oraz przez 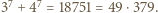
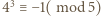 i
i 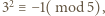 podobnie
podobnie 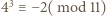 i
i 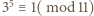 ).
).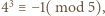 to
to 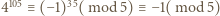 ; podobnie z
; podobnie z 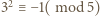 wynika
wynika 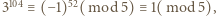 a więc
a więc 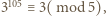 skąd
skąd 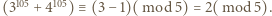
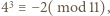 więc
więc 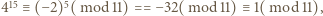 stąd
stąd 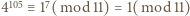 ; podobnie z
; podobnie z 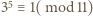 mamy
mamy 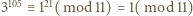 ; wobec tego
; wobec tego 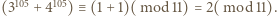
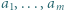 oraz
oraz 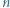 rozważamy sumę
rozważamy sumę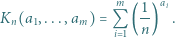
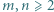 wyznaczyć kres górny zbioru tych wartości wyrażenia
wyznaczyć kres górny zbioru tych wartości wyrażenia 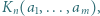 które są mniejsze od 1.
które są mniejsze od 1.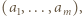 dzięki czemu wyrazy sumy
dzięki czemu wyrazy sumy
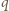 oraz
oraz  oznaczają iloraz i resztę z dzielenia
oznaczają iloraz i resztę z dzielenia 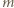 przez
przez 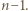 Wykażemy, że ciąg
Wykażemy, że ciąg

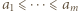 będzie dowolnym ciągiem, dla którego wartość sumy (1) jest mniejsza od 1. Przypuśćmy, że pewien wyraz
będzie dowolnym ciągiem, dla którego wartość sumy (1) jest mniejsza od 1. Przypuśćmy, że pewien wyraz 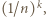 z wykładnikiem
z wykładnikiem 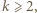 powtarza się co najmniej
powtarza się co najmniej 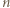 razy. Przyjmijmy, że
razy. Przyjmijmy, że 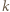 jest największym takim numerem. Wykreślamy
jest największym takim numerem. Wykreślamy 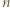 składników równych
składników równych 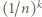 i zastępujemy je pojedynczym wyrazem
i zastępujemy je pojedynczym wyrazem 
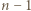 wyrazów. Dopisujemy więc na końcu
wyrazów. Dopisujemy więc na końcu 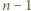 ułamków, z wykładnikami tak dużymi, by wartość sumy (1) (która się powiększa!) pozostała mniejsza od 1 - bacząc jedynie, by żaden wyraz (z wykładnikiem
ułamków, z wykładnikami tak dużymi, by wartość sumy (1) (która się powiększa!) pozostała mniejsza od 1 - bacząc jedynie, by żaden wyraz (z wykładnikiem 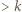 ) nie powtórzył się
) nie powtórzył się 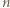 -krotnie.
-krotnie.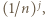 długości co najmniej
długości co najmniej 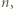 z jakimkolwiek wykładnikiem
z jakimkolwiek wykładnikiem 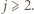 Mógłby ewentualnie pozostać taki blok dla wykładnika
Mógłby ewentualnie pozostać taki blok dla wykładnika 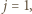 czyli złożony ze składników równych
czyli złożony ze składników równych 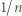 - ale to też nie jest możliwe, skoro przez cały czas była prowadzona kontrola, by suma nie osiągnęła wartości 1. Stąd wynika, że w dalszym ciągu dowodu można ograniczać uwagę do ciągów
- ale to też nie jest możliwe, skoro przez cały czas była prowadzona kontrola, by suma nie osiągnęła wartości 1. Stąd wynika, że w dalszym ciągu dowodu można ograniczać uwagę do ciągów 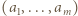 o własnościach:
o własnościach:
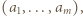 także spełniający powyższe warunki, i oznaczmy przez
także spełniający powyższe warunki, i oznaczmy przez 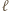 najwcześniejszy numer, dla którego
najwcześniejszy numer, dla którego 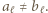 Zatem odcinki
Zatem odcinki 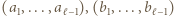 są identyczne.
są identyczne.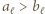 ; w przeciwnym przypadku mielibyśmy
; w przeciwnym przypadku mielibyśmy 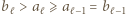 ; to by oznaczało, że
; to by oznaczało, że 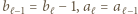 i że w ciągu (2)
i że w ciągu (2) 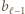 jest wyrazem kończącym blok złożony z
jest wyrazem kończącym blok złożony z 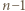 równych liczb. Skoro zaś
równych liczb. Skoro zaś 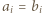 dla
dla 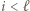 oraz
oraz 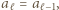 mielibyśmy w ciągu
mielibyśmy w ciągu 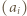 blok złożony z
blok złożony z  równych liczb, wbrew warunkowi (4). Tak więc
równych liczb, wbrew warunkowi (4). Tak więc 
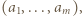 zastępując wyraz
zastępując wyraz 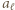 liczbą
liczbą 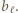 Warunki (4) pozostają spełnione, wartość sumy (1) zwiększa się, zaś nowy ciąg pokrywa się z ciągiem (2) na odcinku
Warunki (4) pozostają spełnione, wartość sumy (1) zwiększa się, zaś nowy ciąg pokrywa się z ciągiem (2) na odcinku 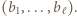 Po skończenie wielu takich krokach dochodzimy do ciągu
Po skończenie wielu takich krokach dochodzimy do ciągu 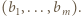 To pokazuje, że wartość sumy (1) dla wyjściowego ciągu
To pokazuje, że wartość sumy (1) dla wyjściowego ciągu 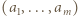 była mniejsza niż jej wartość dla ciągu
była mniejsza niż jej wartość dla ciągu 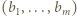 - czyli liczba dana wzorem (3), która wobec tego jest szukanym kresem górnym.
- czyli liczba dana wzorem (3), która wobec tego jest szukanym kresem górnym.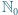 oznacza zbiór nieujemnych liczb całkowitych.
oznacza zbiór nieujemnych liczb całkowitych.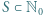 o tej własności, że każdy element zbioru
o tej własności, że każdy element zbioru 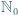 ma dokładnie jedno przedstawienie w postaci sumy dwóch (niekoniecznie różnych) elementów
ma dokładnie jedno przedstawienie w postaci sumy dwóch (niekoniecznie różnych) elementów 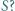
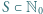 o tej własności, że każdy element niepustego zbioru
o tej własności, że każdy element niepustego zbioru 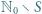 ma dokładnie jedno przedstawienie w postaci sumy dwóch (niekoniecznie różnych) elementów
ma dokładnie jedno przedstawienie w postaci sumy dwóch (niekoniecznie różnych) elementów 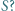
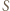 istnieje. Aby liczby 0 oraz
istnieje. Aby liczby 0 oraz 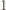 miały przedstawienia w postaci odpowiednich sum, musimy mieć
miały przedstawienia w postaci odpowiednich sum, musimy mieć 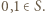 Gdyby
Gdyby 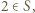 to mielibyśmy dwa przedstawienia tej liczby jako sumy elementów
to mielibyśmy dwa przedstawienia tej liczby jako sumy elementów 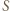 :
: 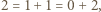 a zatem
a zatem 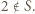 Podobne rozważania prowadzą kolejno do wniosków, że
Podobne rozważania prowadzą kolejno do wniosków, że 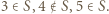 Ale
Ale 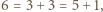 sprzeczność.
sprzeczność.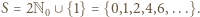 Wówczas każda liczba nieparzysta większa od
Wówczas każda liczba nieparzysta większa od 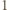 (czyli każdy element zbioru
(czyli każdy element zbioru 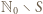 ) postaci
) postaci 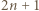 ma dokładnie jedno przedstawienie w postaci sumy dwóch elementów
ma dokładnie jedno przedstawienie w postaci sumy dwóch elementów 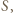 mianowicie
mianowicie 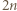 oraz
oraz 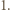
 nazwiemy podkwadratową, jeżeli
nazwiemy podkwadratową, jeżeli 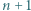 jest kwadratem liczby całkowitej. Wykazać, że istnieje nieskończenie wiele par liczb podkwadratowych o tej własności, że ich suma oraz iloczyn także są podkwadratowe.
jest kwadratem liczby całkowitej. Wykazać, że istnieje nieskończenie wiele par liczb podkwadratowych o tej własności, że ich suma oraz iloczyn także są podkwadratowe.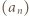 następująco
następująco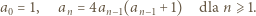
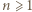 liczba
liczba 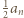 jest kwadratem liczby całkowitej. Dla
jest kwadratem liczby całkowitej. Dla 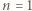 mamy
mamy 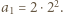 Przypuśćmy, że
Przypuśćmy, że 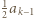 jest kwadratem dla pewnego
jest kwadratem dla pewnego 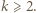 Wówczas
Wówczas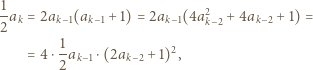
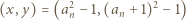
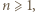 a ponadto pary te są różne, gdyż ciąg
a ponadto pary te są różne, gdyż ciąg 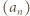 jest ściśle rosnący. Rzeczywiście, mamy
jest ściśle rosnący. Rzeczywiście, mamy 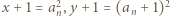 oraz
oraz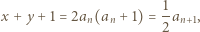
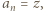 otrzymujemy
otrzymujemy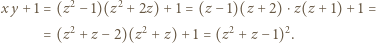
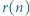 sumę
sumę  liczb będących resztami z dzielenia dodatniej liczby całkowitej
liczb będących resztami z dzielenia dodatniej liczby całkowitej 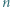 przez
przez 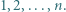 Udowodnij, że istnieje nieskończenie wiele takich
Udowodnij, że istnieje nieskończenie wiele takich 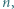 że
że 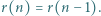
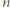 przez liczbę
przez liczbę 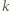 jest równa
jest równa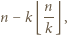
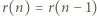 można przepisać jako
można przepisać jako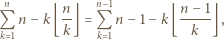
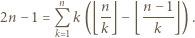
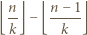
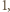 jeżeli
jeżeli 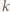 dzieli
dzieli  oraz 0 w przeciwnym przypadku. Stąd wniosek, że powyższy warunek można przepisać jako
oraz 0 w przeciwnym przypadku. Stąd wniosek, że powyższy warunek można przepisać jako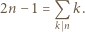
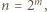 gdzie
gdzie 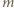 jest dodatnią liczbą całkowitą. Przykładową nieskończoną rodzinę liczb
jest dodatnią liczbą całkowitą. Przykładową nieskończoną rodzinę liczb  spełniających warunek zadania stanowią więc wszystkie potęgi dwójki.
spełniających warunek zadania stanowią więc wszystkie potęgi dwójki.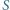 oraz nieskończenie wiele dodatnich liczb całkowitych, które można zapisać w takiej postaci.
oraz nieskończenie wiele dodatnich liczb całkowitych, które można zapisać w takiej postaci.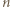 jest liczbą podzielną przez
jest liczbą podzielną przez 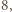 to
to  nie można zapisać w postaci sumy dwóch elementów zbioru
nie można zapisać w postaci sumy dwóch elementów zbioru 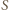 albo - w myśl tezy poprzedniego zadania - w postaci iloczynu dwóch elementów zbioru
albo - w myśl tezy poprzedniego zadania - w postaci iloczynu dwóch elementów zbioru 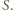 Przypuśćmy, że
Przypuśćmy, że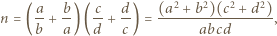
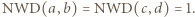 Skoro
Skoro 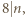 to co najmniej jeden z czynników w liczniku powyższego ułamka jest podzielny przez
to co najmniej jeden z czynników w liczniku powyższego ułamka jest podzielny przez 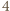 ; bez straty ogólności załóżmy, że
; bez straty ogólności załóżmy, że 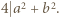 Stąd wynika, że liczby
Stąd wynika, że liczby 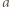 i
i 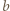 są tej samej parzystości, skąd wobec
są tej samej parzystości, skąd wobec 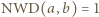 - obie są nieparzyste. Jednak wówczas
- obie są nieparzyste. Jednak wówczas 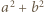 daje resztę
daje resztę 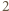 przy dzieleniu przez
przy dzieleniu przez 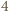 - sprzeczność.
- sprzeczność.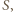 rozważymy ciąg Fibonacciego
rozważymy ciąg Fibonacciego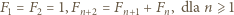
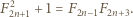
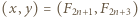 mamy więc
mamy więc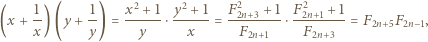
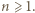 To kończy dowód, gdyż dla różnych
To kończy dowód, gdyż dla różnych 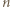 otrzymujemy różne liczby.
otrzymujemy różne liczby.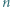 będzie dodatnią liczbą całkowitą. Wykazać, że
będzie dodatnią liczbą całkowitą. Wykazać, że 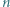 jest sumą dwóch elementów zbioru
jest sumą dwóch elementów zbioru 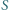 wtedy i tylko wtedy, gdy
wtedy i tylko wtedy, gdy  jest iloczynem dwóch elementów zbioru
jest iloczynem dwóch elementów zbioru 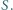
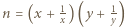 dla pewnych
dla pewnych 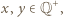 to
to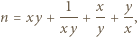
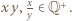 To dowodzi, że jeżeli
To dowodzi, że jeżeli 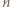 jest iloczynem dwóch elementów zbioru
jest iloczynem dwóch elementów zbioru 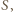 to jest również sumą dwóch elementów zbioru
to jest również sumą dwóch elementów zbioru 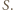
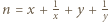 dla pewnych
dla pewnych 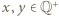 oraz niech
oraz niech 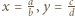 będą zapisami liczb
będą zapisami liczb 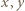 w postaci ułamków nieskracalnych, czyli
w postaci ułamków nieskracalnych, czyli 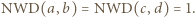 Wówczas
Wówczas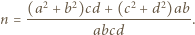
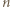 jest liczbą całkowitą, więc
jest liczbą całkowitą, więc 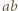 musi być dzielnikiem licznika powyższego ułamka. Stąd wniosek, że
musi być dzielnikiem licznika powyższego ułamka. Stąd wniosek, że 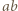 dzieli
dzieli 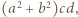 skąd wobec
skąd wobec 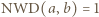 mamy, że
mamy, że 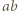 dzieli
dzieli 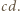 Analogicznie uzasadniamy, że
Analogicznie uzasadniamy, że 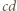 dzieli
dzieli 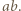 Zatem
Zatem 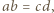 czyli
czyli 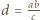 i w konsekwencji
i w konsekwencji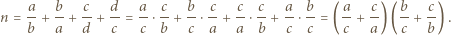
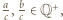 to
to 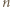 jest iloczynem dwóch elementów zbioru
jest iloczynem dwóch elementów zbioru 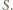
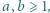 względnie pierwsze i takie, że wzór rekurencyjny
względnie pierwsze i takie, że wzór rekurencyjny
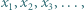 którego wszystkie wyrazy są liczbami złożonymi?
którego wszystkie wyrazy są liczbami złożonymi?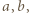 o jakie pyta zadanie, istnieją; można znaleźć wiele takich par. Przykład Autora (W. Bednarek):
o jakie pyta zadanie, istnieją; można znaleźć wiele takich par. Przykład Autora (W. Bednarek): 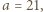
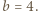 Wówczas
Wówczas 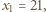
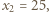 i dalej (dla każdego
i dalej (dla każdego 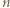 ):
):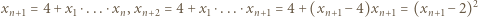
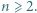
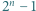 jest bezkwadratowa, to liczby
jest bezkwadratowa, to liczby 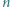 oraz
oraz 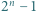 są względnie pierwsze.
są względnie pierwsze. oraz
oraz 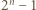 mają wspólny dzielnik pierwszy
mają wspólny dzielnik pierwszy 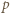 (jasne, że
(jasne, że 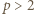 ). Wykażemy, że wówczas liczba
). Wykażemy, że wówczas liczba 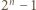 dzieli się przez
dzieli się przez 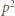 (nie jest więc bezkwadratowa). Zgodnie z małym twierdzeniem Fermata,
(nie jest więc bezkwadratowa). Zgodnie z małym twierdzeniem Fermata, 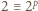 (mod
(mod 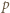 ). Podnosimy tę kongruencję stronami do potęgi
). Podnosimy tę kongruencję stronami do potęgi 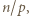 otrzymując
otrzymując 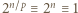 (mod
(mod 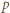 ). Zatem
). Zatem 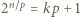 dla pewnej liczby całkowitej
dla pewnej liczby całkowitej 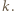 Stąd
Stąd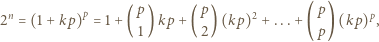
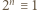 (mod
(mod 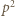 ); a to była nasza teza.
); a to była nasza teza.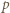 kontroluje dwie końcowe cyfry rozwinięcia (przy podstawie
kontroluje dwie końcowe cyfry rozwinięcia (przy podstawie 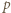 ) kolejnych potęg dwójki, pozwala znaleźć moment powtórzenia końcówki
) kolejnych potęg dwójki, pozwala znaleźć moment powtórzenia końcówki 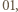 czyli wykładnik
czyli wykładnik 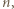 dla którego
dla którego 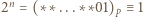 (mod
(mod 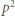 ). Powtarzamy tę procedurę dla kolejnych liczb pierwszych
). Powtarzamy tę procedurę dla kolejnych liczb pierwszych 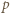 ; warto przy tym, dla oszczędności czasu, ograniczyć zakres wykładnika, np. do
; warto przy tym, dla oszczędności czasu, ograniczyć zakres wykładnika, np. do 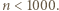 W ten sposób szybko znajdujemy parę
W ten sposób szybko znajdujemy parę 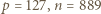 ; nie jest ona jednak szukanym kontrprzykładem, bowiem dla tej pary zachodzą związki
; nie jest ona jednak szukanym kontrprzykładem, bowiem dla tej pary zachodzą związki 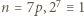 (mod
(mod 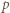 ), z których nietrudno wynika, że liczby
), z których nietrudno wynika, że liczby  i
i 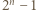 nie są względnie pierwsze.
nie są względnie pierwsze.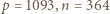 jest już dobra: gdyby liczby
jest już dobra: gdyby liczby 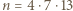 oraz
oraz  nie były względnie pierwsze, ta ostatnia musiałaby się dzielić przez 7 lub 13; ale minimalne wykładniki
nie były względnie pierwsze, ta ostatnia musiałaby się dzielić przez 7 lub 13; ale minimalne wykładniki 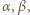 dla których
dla których 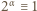 (mod 7),
(mod 7), 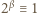 (mod 13), to
(mod 13), to 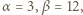 więc wykładnik
więc wykładnik 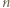 musiałby się dzielić przez 3; a tak nie jest. Skoro zaś ta para została wygenerowana przez algorytm, zapewniający podzielność
musiałby się dzielić przez 3; a tak nie jest. Skoro zaś ta para została wygenerowana przez algorytm, zapewniający podzielność 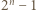 przez
przez 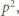 zatem liczba
zatem liczba 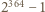 nie jest bezkwadratowa.
nie jest bezkwadratowa.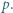 Funkcja
Funkcja 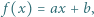 gdzie
gdzie 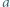 i
i 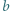 są liczbami całkowitymi, ma tę własność, że liczby
są liczbami całkowitymi, ma tę własność, że liczby
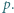 Wykazać, że
Wykazać, że 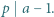
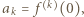 gdzie
gdzie 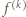 oznacza
oznacza 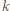 -krotne złożenie funkcji
-krotne złożenie funkcji 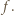 Z warunków zadania wynika, że dla pewnego
Z warunków zadania wynika, że dla pewnego 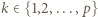 mamy
mamy 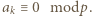 Jeżeli
Jeżeli 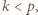 to
to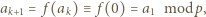
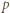 wyrazów ciągu
wyrazów ciągu 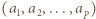 są parami różne. To oznacza, że
są parami różne. To oznacza, że 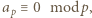 czyli
czyli 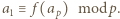
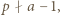 czyli
czyli 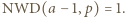 Wówczas istnieją takie liczby całkowite
Wówczas istnieją takie liczby całkowite 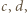 że
że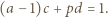
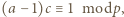 czyli
czyli 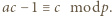 Z warunków zadania wynika, że dla pewnego
Z warunków zadania wynika, że dla pewnego 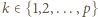 mamy
mamy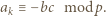
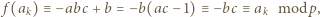
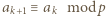 (gdzie w razie potrzeby przyjmujemy
(gdzie w razie potrzeby przyjmujemy 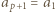 ). To stoi w sprzeczności z założeniem, że reszty z dzielenia przez
). To stoi w sprzeczności z założeniem, że reszty z dzielenia przez 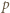 wyrazów ciągu
wyrazów ciągu 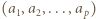 są parami różne.
są parami różne.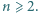 Wykazać, że dla każdego układu dodatnich liczb całkowitych
Wykazać, że dla każdego układu dodatnich liczb całkowitych 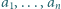 zachodzi nierówność
zachodzi nierówność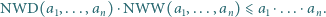
 ) te układy
) te układy 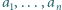 (dodatnich liczb całkowitych), dla których napisana nierówność staje się równością.
(dodatnich liczb całkowitych), dla których napisana nierówność staje się równością.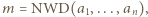
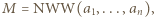
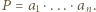 Wystarczy wykazać, że każda liczba pierwsza, która dzieli iloczyn
Wystarczy wykazać, że każda liczba pierwsza, która dzieli iloczyn 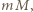 wchodzi do iloczynu
wchodzi do iloczynu 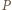 w co najmniej takiej samej potędze. Niech więc
w co najmniej takiej samej potędze. Niech więc 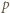 będzie liczbą pierwszą i niech (dla
będzie liczbą pierwszą i niech (dla 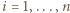 )
) 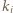 będzie takim wykładnikiem, że
będzie takim wykładnikiem, że 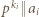 (ten napis oznacza, że
(ten napis oznacza, że 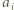 dzieli się przez
dzieli się przez 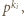 ale nie przez
ale nie przez 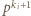 ). Wówczas
). Wówczas 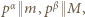 gdzie
gdzie 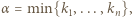
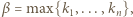 i wobec tego
i wobec tego 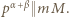 Oczywiście
Oczywiście 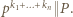 Porównanie wykładników nie pozostawia wątpliwości:
Porównanie wykładników nie pozostawia wątpliwości:
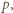 uzasadnia to zadaną nierówność
uzasadnia to zadaną nierówność 
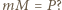 Wtedy, gdy każda liczba pierwsza dzieli
Wtedy, gdy każda liczba pierwsza dzieli 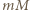 w dokładnie tej samej potędze, w jakiej dzieli
w dokładnie tej samej potędze, w jakiej dzieli 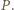 Czyli gdy dla każdej liczby pierwszej
Czyli gdy dla każdej liczby pierwszej 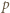 nierówność (1) (z wykładnikami
nierówność (1) (z wykładnikami 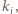 wyznaczonymi przez
wyznaczonymi przez 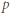 ) staje się równością.
) staje się równością.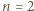 jest tak zawsze; dostajemy znaną tożsamość:
jest tak zawsze; dostajemy znaną tożsamość: 
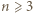 równość w relacji (1) oznacza, że gdy po jej prawej stronie usuniemy jeden największy i jeden najmniejszy składnik, pozostaną jakieś nieskreślone składniki, o zerowej sumie - czyli wszystkie równe zeru. Składnik najmniejszy automatycznie także jest zerem. Tylko jeden składnik po prawej stronie (1) może być dodatni. To znaczy, że tylko jedna z liczb
równość w relacji (1) oznacza, że gdy po jej prawej stronie usuniemy jeden największy i jeden najmniejszy składnik, pozostaną jakieś nieskreślone składniki, o zerowej sumie - czyli wszystkie równe zeru. Składnik najmniejszy automatycznie także jest zerem. Tylko jeden składnik po prawej stronie (1) może być dodatni. To znaczy, że tylko jedna z liczb 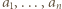 może dzielić się przez
może dzielić się przez 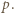 Wobec dowolności
Wobec dowolności 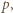 znaczy to, że liczby
znaczy to, że liczby 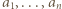 są parami względnie pierwsze.
są parami względnie pierwsze.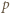 mamy w ciągu
mamy w ciągu 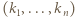 co najwyżej jeden wyraz niezerowy; nierównść (1) przechodzi w równość, i w konsekwencji
co najwyżej jeden wyraz niezerowy; nierównść (1) przechodzi w równość, i w konsekwencji 
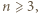 równość
równość 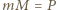 zachodzi wtedy i tylko wtedy, gdy liczby
zachodzi wtedy i tylko wtedy, gdy liczby 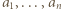 są parami względnie pierwsze; dla
są parami względnie pierwsze; dla 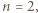 ta równość jest tożsamością.
ta równość jest tożsamością.