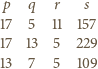Przyjmijmy, że liczby 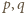 spełniają postawione warunki; w szczególności
spełniają postawione warunki; w szczególności 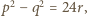 gdzie
gdzie  jest liczbą pierwszą. Jasne, że
jest liczbą pierwszą. Jasne, że 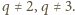 Iloczyn liczb naturalnych
Iloczyn liczb naturalnych 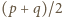 i
i 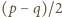 wynosi
wynosi 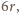 więc jedna z nich dzieli się przez
więc jedna z nich dzieli się przez 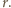 W takim razie druga jest dzielnikiem liczby 6; wobec czego mniejsza z nich nie przekracza 6. Dostajemy oszacowanie
W takim razie druga jest dzielnikiem liczby 6; wobec czego mniejsza z nich nie przekracza 6. Dostajemy oszacowanie 
Jeżeli 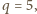 to
to 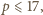 czyli
czyli 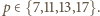 Sprawdzamy, że tylko para
Sprawdzamy, że tylko para 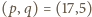 jest dobra.
jest dobra.
Dalej przyjmujemy, że 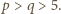 Wówczas
Wówczas 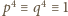 (mod 5), więc
(mod 5), więc
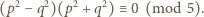
To pokazuje, że iloczyn liczb całkowitych 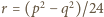 oraz
oraz 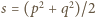 dzieli się przez 5. Są to z założenia liczby pierwsze, więc któraś z nich jest równa 5. Ale
dzieli się przez 5. Są to z założenia liczby pierwsze, więc któraś z nich jest równa 5. Ale 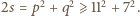 Pozostaje możliwość
Pozostaje możliwość 
Iloczyn liczb naturalnych 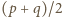 i
i 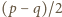 wynosi
wynosi 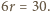 Cztery możliwe rozkłady
Cztery możliwe rozkłady 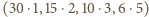 dają pary
dają pary 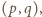 odpowiednio,
odpowiednio, 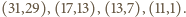 Ostatnia odpada. Dla
Ostatnia odpada. Dla 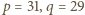 wychodzi
wychodzi 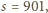 liczba złożona. Pozostałe dwie pary są już dobre. Wraz z parą znalezioną wcześniej, ostatecznie otrzymujemy trzy rozwiązania. Wypiszemy je, podając również wartości
liczba złożona. Pozostałe dwie pary są już dobre. Wraz z parą znalezioną wcześniej, ostatecznie otrzymujemy trzy rozwiązania. Wypiszemy je, podając również wartości  i
i  :
:
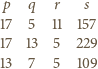
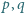
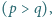 dla których także liczby
dla których także liczby 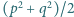 oraz
oraz 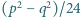 są pierwsze.
są pierwsze.
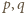 spełniają postawione warunki; w szczególności
spełniają postawione warunki; w szczególności 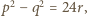 gdzie
gdzie  jest liczbą pierwszą. Jasne, że
jest liczbą pierwszą. Jasne, że 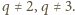 Iloczyn liczb naturalnych
Iloczyn liczb naturalnych 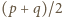 i
i 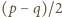 wynosi
wynosi 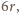 więc jedna z nich dzieli się przez
więc jedna z nich dzieli się przez 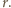 W takim razie druga jest dzielnikiem liczby 6; wobec czego mniejsza z nich nie przekracza 6. Dostajemy oszacowanie
W takim razie druga jest dzielnikiem liczby 6; wobec czego mniejsza z nich nie przekracza 6. Dostajemy oszacowanie 
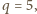 to
to 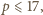 czyli
czyli 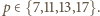 Sprawdzamy, że tylko para
Sprawdzamy, że tylko para 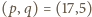 jest dobra.
jest dobra.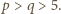 Wówczas
Wówczas 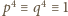 (mod 5), więc
(mod 5), więc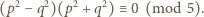
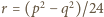 oraz
oraz 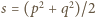 dzieli się przez 5. Są to z założenia liczby pierwsze, więc któraś z nich jest równa 5. Ale
dzieli się przez 5. Są to z założenia liczby pierwsze, więc któraś z nich jest równa 5. Ale 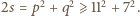 Pozostaje możliwość
Pozostaje możliwość 
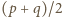 i
i 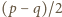 wynosi
wynosi 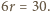 Cztery możliwe rozkłady
Cztery możliwe rozkłady 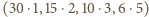 dają pary
dają pary 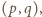 odpowiednio,
odpowiednio, 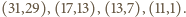 Ostatnia odpada. Dla
Ostatnia odpada. Dla 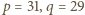 wychodzi
wychodzi 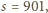 liczba złożona. Pozostałe dwie pary są już dobre. Wraz z parą znalezioną wcześniej, ostatecznie otrzymujemy trzy rozwiązania. Wypiszemy je, podając również wartości
liczba złożona. Pozostałe dwie pary są już dobre. Wraz z parą znalezioną wcześniej, ostatecznie otrzymujemy trzy rozwiązania. Wypiszemy je, podając również wartości  i
i  :
: