Zadanie ZM-1572
o zadaniu...
- Publikacja w Delcie: lipiec 2018
- Publikacja elektroniczna: 30 czerwca 2018
Oznaczmy przez 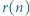 sumę
sumę  liczb będących resztami z dzielenia dodatniej liczby całkowitej
liczb będących resztami z dzielenia dodatniej liczby całkowitej 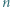 przez
przez 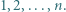 Udowodnij, że istnieje nieskończenie wiele takich
Udowodnij, że istnieje nieskończenie wiele takich 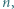 że
że 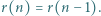

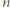 przez liczbę
przez liczbę 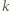 jest równa
jest równa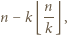
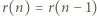 można przepisać jako
można przepisać jako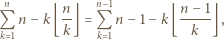
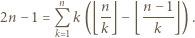
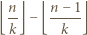
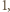 jeżeli
jeżeli 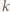 dzieli
dzieli  oraz 0 w przeciwnym przypadku. Stąd wniosek, że powyższy warunek można przepisać jako
oraz 0 w przeciwnym przypadku. Stąd wniosek, że powyższy warunek można przepisać jako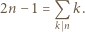
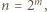 gdzie
gdzie 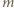 jest dodatnią liczbą całkowitą. Przykładową nieskończoną rodzinę liczb
jest dodatnią liczbą całkowitą. Przykładową nieskończoną rodzinę liczb  spełniających warunek zadania stanowią więc wszystkie potęgi dwójki.
spełniających warunek zadania stanowią więc wszystkie potęgi dwójki.