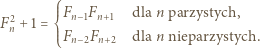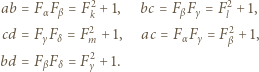Klub 44M - zadania IX 2019»Zadanie 786
o zadaniu...
- Zadanie pochodzi z artykułu Klub 44M - zadania IX 2019
- Publikacja w Delcie: wrzesień 2019
- Publikacja elektroniczna: 1 września 2019
- Artykuł źródłowy w wersji do druku [application/pdf]: (310 KB)
-
Zadanie 786 zaproponował pan Witold Bednarek z Łodzi.
Dowieść, że istnieje nieskończenie wiele czwórek różnych liczb naturalnych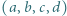 
o tej własności, że każdy z iloczynów 
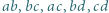jest o 1 większy od kwadratu pewnej liczby naturalnej.
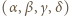jest dowolną czwórką kolejnych liczb naturalnych nieparzystych, wówczas czwórka 
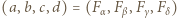jest dobra; jak zwykle, 
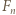oznacza 
-tą liczbę Fibonacciego ( 
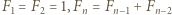dla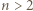 
).
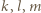do pełnego bloku siedmiu kolejnych liczb naturalnych 
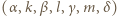i korzystamy ze znanych tożsamości
