Zadanie ZM-1552
o zadaniu...
- Publikacja w Delcie: styczeń 2018
- Publikacja elektroniczna: 1 stycznia 2018
Wykazać, że istnieje nieskończenie wiele par liczb całkowitych dodatnich 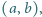 dla których liczba
dla których liczba

jest kwadratem liczby całkowitej.
Wykazać, że istnieje nieskończenie wiele par liczb całkowitych dodatnich 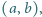 dla których liczba
dla których liczba

jest kwadratem liczby całkowitej.
Wykazać, że każdą dodatnią liczbę całkowitą można zapisać w postaci różnicy dwóch dodatnich liczb całkowitych, które mają tę samą liczbę różnych dzielników pierwszych.
Zadanie 752 zaproponował pan Witold Bednarek z Łodzi.
Znaleźć wszystkie pary liczb całkowitych dodatnich, których średnia arytmetyczna i średnia geometryczna różnią się o 1.
Zadanie 750 zaproponował pan Tomasz Ordowski.
Znaleźć wszystkie pary liczb pierwszych 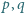
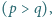 dla których także liczby
dla których także liczby 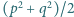 oraz
oraz 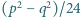 są pierwsze.
są pierwsze.
Niech  będzie takim podzbiorem zbioru
będzie takim podzbiorem zbioru  dodatnich liczb całkowitych, że dla każdej pary
dodatnich liczb całkowitych, że dla każdej pary 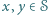 również
również 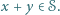 Przypuśćmy, że zbiór
Przypuśćmy, że zbiór 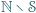 jest skończony i
jest skończony i 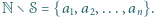 Udowodnić, że
Udowodnić, że

Znaleźć wszystkie nieujemne liczby całkowite 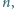 dla których każda z liczb
dla których każda z liczb 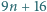 oraz
oraz 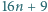 jest kwadratem liczby całkowitej.
jest kwadratem liczby całkowitej.
Największy wspólny dzielnik liczb całkowitych dodatnich 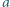 i
i 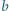 jest równy
jest równy 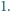 Dowieść, że największy wspólny dzielnik liczb
Dowieść, że największy wspólny dzielnik liczb 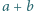 i
i 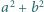 nie przekracza
nie przekracza 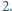
Znaleźć największą liczbę naturalną 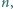 dla której
dla której 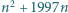 jest kwadratem liczby naturalnej.
jest kwadratem liczby naturalnej.
Zadanie 742 zaproponował pan Tomasz Ordowski.
Niech 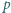 będzie liczbą pierwszą postaci
będzie liczbą pierwszą postaci 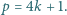 Dowieść, że istnieje liczba całkowita dodatnia
Dowieść, że istnieje liczba całkowita dodatnia 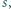 mniejsza od
mniejsza od 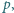 dla której różnica
dla której różnica 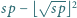 jest kwadratem liczby całkowitej dodatniej.
jest kwadratem liczby całkowitej dodatniej.
Udowodnić, że jeżeli dla pewnej liczby naturalnej 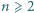 liczba
liczba 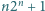 jest pierwsza, to liczby
jest pierwsza, to liczby 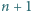 oraz
oraz 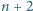 są złożone.
są złożone.
Udowodnić, że dla każdego 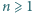 istnieje ciąg arytmetyczny
istnieje ciąg arytmetyczny  dodatnich liczb całkowitych, z których każda jest podzielna przez sumę swoich cyfr (w zapisie dziesiętnym).
dodatnich liczb całkowitych, z których każda jest podzielna przez sumę swoich cyfr (w zapisie dziesiętnym).
Wskazówka. W rozwiązaniu można skorzystać z twierdzenia o liczbach pierwszych, na przykład używając szacowania 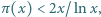 prawdziwego dla dostatecznie dużych
prawdziwego dla dostatecznie dużych 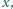 gdzie
gdzie 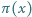 oznacza liczbę liczb pierwszych nie większych od
oznacza liczbę liczb pierwszych nie większych od 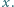
Zadanie 738 zaproponował pan Bartłomiej Pawlik z Limanowej.
Wypisując, jedna za drugą, wszystkie liczby całkowite dodatnie, mające (w systemie dziesiętnym) co najwyżej 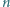 cyfr, piszemy łącznie
cyfr, piszemy łącznie 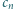 cyfr (np.
cyfr (np. 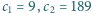 ); w tym
); w tym 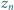 zer (np.
zer (np. 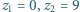 ). Czy równość
). Czy równość 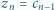 jest spełniona dla wszystkich liczb naturalnych
jest spełniona dla wszystkich liczb naturalnych 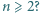
Przypuśćmy, że dla pewnej dodatniej liczby całkowitej 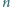 liczby
liczby 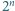 oraz
oraz 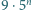 rozpoczynają się w zapisie dziesiętnym tą samą cyfrą. Jaka to cyfra?
rozpoczynają się w zapisie dziesiętnym tą samą cyfrą. Jaka to cyfra?
Każdą liczbę całkowitą większą od 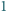 pomalowano na pewien kolor w taki sposób, że jeżeli dla pewnych dwóch liczb
pomalowano na pewien kolor w taki sposób, że jeżeli dla pewnych dwóch liczb 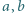 większych od
większych od 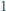 liczba
liczba 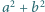 jest podzielna przez
jest podzielna przez 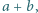 to
to 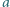 ma ten sam kolor, co
ma ten sam kolor, co 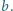 Jaka jest największa możliwa liczba kolorów użytych do pomalowania liczb?
Jaka jest największa możliwa liczba kolorów użytych do pomalowania liczb?
Udowodnij, że dla każdej niepodzielnej przez 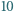 liczby naturalnej
liczby naturalnej 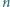 istnieje taka liczba naturalna
istnieje taka liczba naturalna 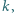 że pierwsza i ostatnia cyfra liczby
że pierwsza i ostatnia cyfra liczby 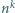 są równe.
są równe.
Zadanie 732 zaproponował pan Tomasz Ordowski.
Ciąg liczb naturalnych 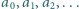 jest określony wzorem rekurencyjnym:
jest określony wzorem rekurencyjnym: 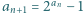 ; wyraz początkowy
; wyraz początkowy 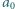 jest liczbą pierwszą. Dowieść, że dla każdego
jest liczbą pierwszą. Dowieść, że dla każdego 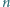 różnica
różnica 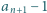 jest podzielna przez
jest podzielna przez 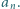
Znaleźć wszystkie liczby całkowite 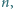 dla których liczba
dla których liczba 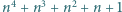 jest kwadratem liczby całkowitej.
jest kwadratem liczby całkowitej.
Obliczyć sumę
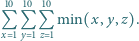
Zadanie 726 zaproponował pan Tomasz Ordowski.
Niech  będzie ustaloną liczbą całkowitą dodatnią. Dowieść, że istnieje nieujemna liczba całkowita
będzie ustaloną liczbą całkowitą dodatnią. Dowieść, że istnieje nieujemna liczba całkowita 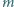 taka, że
taka, że 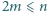 oraz różnica
oraz różnica 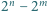 dzieli się przez
dzieli się przez 
Czy istnieje taka liczba 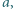 że jej suma cyfr w systemie dziesiętnym jest równa
że jej suma cyfr w systemie dziesiętnym jest równa 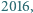 a suma cyfr liczby
a suma cyfr liczby 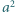 jest równa
jest równa 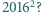
Czy istnieje wielokrotność liczby 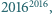 której zapis w systemie dziesiętnym zawiera wszystkie dziesięć cyfr?
której zapis w systemie dziesiętnym zawiera wszystkie dziesięć cyfr?
Każda z liczb całkowitych 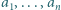 jest mniejsza od
jest mniejsza od 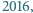 a najmniejsza wspólna wielokrotność dowolnych dwóch z tych liczb jest większa od
a najmniejsza wspólna wielokrotność dowolnych dwóch z tych liczb jest większa od 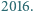 Wykazać, że
Wykazać, że

Czy każdy ściśle rosnący ciąg arytmetyczny o wyrazach całkowitych ma wyraz, będący jednocześnie pewnym wyrazem ciągu Fibonacciego 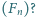

Zadanie 722 zaproponował pan Witold Bednarek z Łodzi.
Rozwiązać równanie 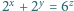 w liczbach całkowitych dodatnich
w liczbach całkowitych dodatnich 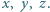
Wyznaczyć największą liczbę naturalną 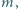 dla której istnieją takie liczby naturalne
dla której istnieją takie liczby naturalne 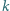 i
i 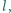 że spełnione jest równanie
że spełnione jest równanie
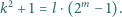
W wierzchołkach dwunastościanu foremnego umieszczamy parami różne liczby naturalne, a następnie każdej krawędzi przypisujemy największy wspólny dzielnik liczb z jej końców. Czy możemy zrobić to w taki sposób, by suma liczb w wierzchołkach była równa sumie liczb na krawędziach?
Udowodnić, że istnieje 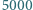 liczb
liczb 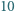 -cyfrowych podzielnych przez
-cyfrowych podzielnych przez 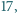 takich że każdą z nich można otrzymać z dowolnej z pozostałych poprzez zmianę kolejności cyfr.
takich że każdą z nich można otrzymać z dowolnej z pozostałych poprzez zmianę kolejności cyfr.
Znaleźć liczbę wielokrotności 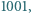 które można zapisać w postaci
które można zapisać w postaci 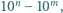 gdzie
gdzie  oraz
oraz 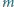 są liczbami całkowitymi spełniającymi
są liczbami całkowitymi spełniającymi 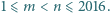
Rozstrzygnąć, czy istnieją liczby naturalne 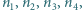 wszystkie większe od
wszystkie większe od 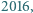 spełniające równanie
spełniające równanie

Dane są takie liczby całkowite dodatnie 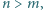 że liczby
że liczby 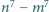 oraz
oraz 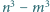 są względnie pierwsze. Wykaż, że liczby
są względnie pierwsze. Wykaż, że liczby 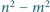 i
i 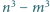 są również względnie pierwsze.
są również względnie pierwsze.