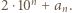Załóżmy, że dodatnie liczby całkowite 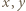 spełniają podane równanie. Oznaczmy przez
spełniają podane równanie. Oznaczmy przez 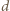 ich największy wspólny dzielnik; tak więc
ich największy wspólny dzielnik; tak więc 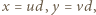 gdzie
gdzie 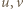 to liczby naturalne względnie pierwsze. Wstawiając to do równania i dzieląc stronami przez
to liczby naturalne względnie pierwsze. Wstawiając to do równania i dzieląc stronami przez 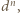 otrzymujemy
otrzymujemy
 |
(1) |
Niech 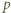 będzie dowolnym dzielnikiem pierwszym liczby
będzie dowolnym dzielnikiem pierwszym liczby 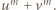 Wobec związku (1)
Wobec związku (1) 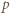 jest też dzielnikiem sumy
jest też dzielnikiem sumy 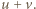 To znaczy, że
To znaczy, że 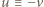 (mod
(mod 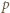 ); a skoro
); a skoro 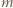 jest liczbą parzystą, mamy stąd
jest liczbą parzystą, mamy stąd 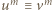 (mod
(mod 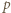 ), i dalej
), i dalej
Liczba  nie dzieli się przez
nie dzieli się przez 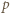 (bo
(bo 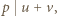 zaś
zaś 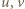 są względnie pierwsze); zatem
są względnie pierwsze); zatem 
Skoro 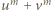 nie ma innych dzielników pierwszych, znaczy to, że
nie ma innych dzielników pierwszych, znaczy to, że
 |
(2) |
Zatem liczby 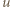 i
i  (względnie pierwsze) są obie nieparzyste; stąd
(względnie pierwsze) są obie nieparzyste; stąd 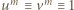 (mod 4), bo
(mod 4), bo 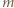 jest liczbą parzystą. W równości (2) mamy więc
jest liczbą parzystą. W równości (2) mamy więc 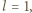 skąd
skąd 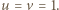 Wracamy do równania (1):
Wracamy do równania (1): 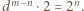 To pokazuje, że
To pokazuje, że 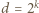 (dla pewnego
(dla pewnego 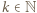 ); przy tym
); przy tym 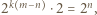 czyli
czyli 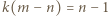 : liczba
: liczba 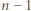 dzieli się przez
dzieli się przez 
Na odwrót, załóżmy, że 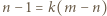 dla pewnego
dla pewnego 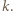 Wówczas para
Wówczas para 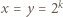 jest rozwiązaniem zadanego równania:
jest rozwiązaniem zadanego równania:
Uzyskaliśmy żądaną równoważność.
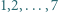 występuje dokładnie raz. Udowodnić, że żadna z tych liczb nie jest dzielnikiem innej.
występuje dokładnie raz. Udowodnić, że żadna z tych liczb nie jest dzielnikiem innej.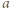 i
i 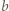 spośród danych w zadaniu. Mamy
spośród danych w zadaniu. Mamy 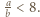 Jeśli
Jeśli 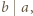 to niech
to niech 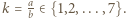 Wówczas
Wówczas 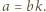 Teraz trzeba zauważyć, że liczby
Teraz trzeba zauważyć, że liczby 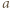 i
i 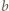 dają resztę 1 z dzielenia przez 9, co wymusza
dają resztę 1 z dzielenia przez 9, co wymusza 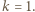
 nie występuje żadna z cyfr 1, 2, 9. Udowodnić, że w zapisie dziesiętnym liczby
nie występuje żadna z cyfr 1, 2, 9. Udowodnić, że w zapisie dziesiętnym liczby 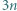 występuje co najmniej jedna z tych cyfr.
występuje co najmniej jedna z tych cyfr.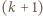 -cyfrowa. Możemy zapisać
-cyfrowa. Możemy zapisać 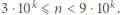 Wystarczy teraz wykazać, że jeśli liczba
Wystarczy teraz wykazać, że jeśli liczba 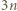 ma tyle samo cyfr co
ma tyle samo cyfr co 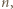 to jej pierwszą cyfrą jest 9, a jeśli ma o jedną cyfrę więcej, to jej pierwszą cyfrą jest 1 lub 2.
to jej pierwszą cyfrą jest 9, a jeśli ma o jedną cyfrę więcej, to jej pierwszą cyfrą jest 1 lub 2.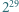 jest dziewięć cyfr, każda inna. Wiedząc to, bez obliczania
jest dziewięć cyfr, każda inna. Wiedząc to, bez obliczania 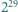 wyznaczyć cyfrę, która w tej liczbie nie występuje.
wyznaczyć cyfrę, która w tej liczbie nie występuje.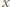 jest brakującą cyfrą, to suma cyfr liczby
jest brakującą cyfrą, to suma cyfr liczby 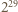 wynosi
wynosi 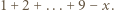 Zauważmy, że liczba
Zauważmy, że liczba 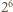 daje resztę 1 z dzielenia przez 9, więc liczba
daje resztę 1 z dzielenia przez 9, więc liczba 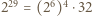 daje resztę 5 z dzielenia przez 9. Wystarczy porównać obie reszty.
daje resztę 5 z dzielenia przez 9. Wystarczy porównać obie reszty.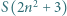 nie jest kwadratem liczby całkowitej dla żadnego naturalnego
nie jest kwadratem liczby całkowitej dla żadnego naturalnego 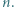
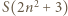 daje taką samą resztę z dzielenia przez 9, co
daje taką samą resztę z dzielenia przez 9, co 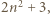 czyli 2, 3, 5 lub 8.
czyli 2, 3, 5 lub 8.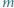 i
i 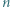 zachodzi nierówność
zachodzi nierówność 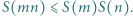
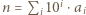 i
i 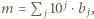 otrzymamy
otrzymamy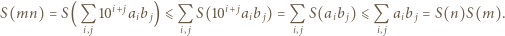
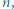 które spełniają równość
które spełniają równość 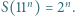
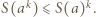 Wobec tego dla
Wobec tego dla 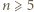 zachodzą nierówności
zachodzą nierówności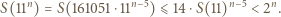
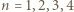 mamy
mamy 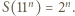
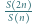 dla całkowitych dodatnich
dla całkowitych dodatnich 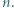

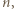 dla których osiągane są skrajne wartości.
dla których osiągane są skrajne wartości.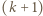 -cyfrową
-cyfrową 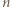 o pierwszej cyfrze
o pierwszej cyfrze 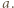 Iloczyn cyfr liczby
Iloczyn cyfr liczby 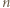 nie przekracza
nie przekracza 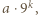 natomiast
natomiast 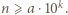 Taka liczba nie istnieje.
Taka liczba nie istnieje. liczby
liczby 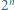 i
i 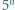 mają taką samą pierwszą cyfrę. Wykazać, że tą cyfrą jest 3.
mają taką samą pierwszą cyfrę. Wykazać, że tą cyfrą jest 3. będzie pierwszą cyfrą
będzie pierwszą cyfrą 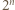 i
i 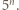 Zapiszmy
Zapiszmy 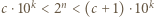 oraz
oraz 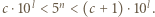 Mnożąc te dwie nierówności, otrzymamy
Mnożąc te dwie nierówności, otrzymamy 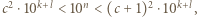 z czego wnioskujemy, że
z czego wnioskujemy, że 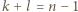 i w konsekwencji
i w konsekwencji 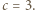
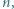 dla których
dla których 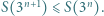
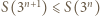 zachodzi tylko dla skończenie wielu
zachodzi tylko dla skończenie wielu 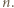 Wtedy istnieje takie
Wtedy istnieje takie 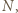 że dla wszystkich
że dla wszystkich 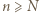 mamy
mamy 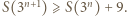 Stąd dla wszystkich
Stąd dla wszystkich 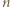 zachodzi nierówność
zachodzi nierówność 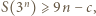 gdzie
gdzie  jest pewną stałą. Z drugiej strony,
jest pewną stałą. Z drugiej strony, 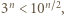 więc liczba
więc liczba 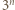 ma co najwyżej
ma co najwyżej 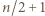 cyfr.
cyfr.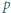 będzie liczbą pierwszą większą od 2. Udowodnić, że istnieje dokładnie jeden sposób przedstawienia
będzie liczbą pierwszą większą od 2. Udowodnić, że istnieje dokładnie jeden sposób przedstawienia 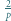 w postaci sumy
w postaci sumy 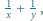 gdzie
gdzie 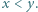
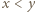 spełniają
spełniają 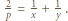 Równanie to można sprowadzić do postaci
Równanie to można sprowadzić do postaci 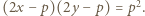 Ponieważ
Ponieważ 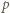 jest liczbą pierwszą, wynika stąd, że
jest liczbą pierwszą, wynika stąd, że 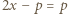 lub
lub 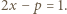 Pierwsza z tych możliwości oznaczałaby, że
Pierwsza z tych możliwości oznaczałaby, że 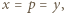 co przeczy zależności
co przeczy zależności 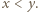 Musi być zatem
Musi być zatem 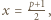 skąd
skąd 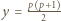 ; ponieważ
; ponieważ 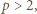 liczby te są całkowite i faktycznie spełniają wymaganą równość.
liczby te są całkowite i faktycznie spełniają wymaganą równość.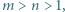 przy czym
przy czym 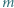 jest liczbą parzystą. Udowodnić, że równanie
jest liczbą parzystą. Udowodnić, że równanie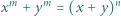
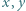 wtedy i tylko wtedy, gdy
wtedy i tylko wtedy, gdy 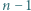 dzieli się przez
dzieli się przez 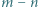 .
.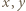 spełniają podane równanie. Oznaczmy przez
spełniają podane równanie. Oznaczmy przez 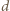 ich największy wspólny dzielnik; tak więc
ich największy wspólny dzielnik; tak więc 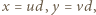 gdzie
gdzie 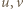 to liczby naturalne względnie pierwsze. Wstawiając to do równania i dzieląc stronami przez
to liczby naturalne względnie pierwsze. Wstawiając to do równania i dzieląc stronami przez 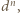 otrzymujemy
otrzymujemy
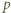 będzie dowolnym dzielnikiem pierwszym liczby
będzie dowolnym dzielnikiem pierwszym liczby 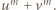 Wobec związku (1)
Wobec związku (1) 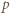 jest też dzielnikiem sumy
jest też dzielnikiem sumy 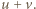 To znaczy, że
To znaczy, że 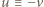 (mod
(mod 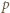 ); a skoro
); a skoro 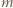 jest liczbą parzystą, mamy stąd
jest liczbą parzystą, mamy stąd 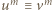 (mod
(mod 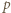 ), i dalej
), i dalej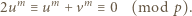
 nie dzieli się przez
nie dzieli się przez 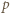 (bo
(bo 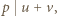 zaś
zaś 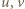 są względnie pierwsze); zatem
są względnie pierwsze); zatem 
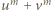 nie ma innych dzielników pierwszych, znaczy to, że
nie ma innych dzielników pierwszych, znaczy to, że
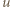 i
i  (względnie pierwsze) są obie nieparzyste; stąd
(względnie pierwsze) są obie nieparzyste; stąd 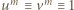 (mod 4), bo
(mod 4), bo 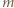 jest liczbą parzystą. W równości (2) mamy więc
jest liczbą parzystą. W równości (2) mamy więc 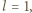 skąd
skąd 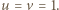 Wracamy do równania (1):
Wracamy do równania (1): 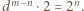 To pokazuje, że
To pokazuje, że 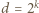 (dla pewnego
(dla pewnego 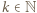 ); przy tym
); przy tym 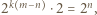 czyli
czyli 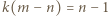 : liczba
: liczba 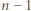 dzieli się przez
dzieli się przez 
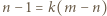 dla pewnego
dla pewnego 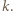 Wówczas para
Wówczas para 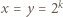 jest rozwiązaniem zadanego równania:
jest rozwiązaniem zadanego równania: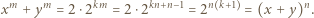
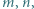 przy czym
przy czym 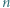 jest liczbą nieparzystą, większą niż
jest liczbą nieparzystą, większą niż 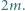 Udowodnić, że liczba
Udowodnić, że liczba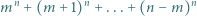
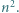
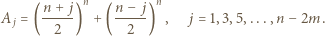
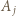 dzieli się przez
dzieli się przez 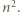 W rozwinięciu dwumianowym
W rozwinięciu dwumianowym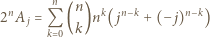
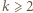 są podzielne przez
są podzielne przez 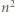 ; skoro zaś
; skoro zaś 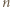 jest liczbą nieparzystą, dwa składniki początkowe dają w sumie
jest liczbą nieparzystą, dwa składniki początkowe dają w sumie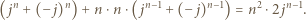
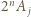 dzieli się przez
dzieli się przez 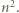 Korzystając jeszcze raz z nieparzystości
Korzystając jeszcze raz z nieparzystości 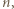 wnosimy, że
wnosimy, że 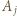 dzieli się przez
dzieli się przez 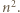
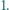 Jeśli na tablicy napisana jest co najmniej jedna z liczb
Jeśli na tablicy napisana jest co najmniej jedna z liczb 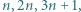 to można dopisać każdą z pozostałych. Rozstrzygnąć, czy każda dodatnia liczba całkowita może w pewnym momencie pojawić się na tablicy.
to można dopisać każdą z pozostałych. Rozstrzygnąć, czy każda dodatnia liczba całkowita może w pewnym momencie pojawić się na tablicy.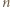 mogła zostać uzyskana (poprzez ciąg kilku kolejnych dopisywań) z pewnej mniejszej liczby. Stąd dostaniemy odpowiedź twierdzącą na postawione w zadaniu pytanie.
mogła zostać uzyskana (poprzez ciąg kilku kolejnych dopisywań) z pewnej mniejszej liczby. Stąd dostaniemy odpowiedź twierdzącą na postawione w zadaniu pytanie.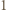 z dzielenia przez
z dzielenia przez 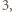 powiedzmy
powiedzmy 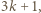 można uzyskać w jednym kroku z liczby
można uzyskać w jednym kroku z liczby 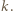 Liczba dająca resztę
Liczba dająca resztę 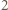 z dzielenia przez
z dzielenia przez 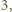 powiedzmy
powiedzmy 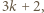 może zostać uzyskana w dwóch krokach z liczby
może zostać uzyskana w dwóch krokach z liczby 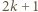 : w pierwszym kroku dopisujemy liczbę
: w pierwszym kroku dopisujemy liczbę 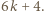 Wreszcie liczba podzielna przez
Wreszcie liczba podzielna przez 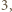 powiedzmy
powiedzmy 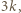 może zostać uzyskana w siedmiu krokach z liczby
może zostać uzyskana w siedmiu krokach z liczby 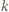 : w kolejnych pośrednich krokach dopisujemy
: w kolejnych pośrednich krokach dopisujemy 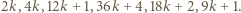
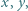 że
że 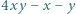 jest kwadratem liczby całkowitej.
jest kwadratem liczby całkowitej.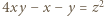 dla pewnych liczb całkowitych
dla pewnych liczb całkowitych 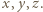 Równość tę możemy przepisać do postaci
Równość tę możemy przepisać do postaci 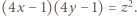 Niech
Niech 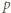 będzie dzielnikiem pierwszym
będzie dzielnikiem pierwszym 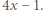 Wówczas
Wówczas 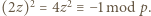 Z Małego Twierdzenia Fermata wiemy, że
Z Małego Twierdzenia Fermata wiemy, że 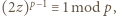 a zatem
a zatem 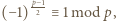 co oznacza że
co oznacza że 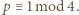 Ponieważ
Ponieważ 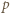 było dowolnym dzielnikiem pierwszym
było dowolnym dzielnikiem pierwszym 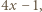 więc
więc 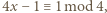 a to jest sprzeczność.
a to jest sprzeczność.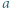 jest cyfrą setek,
jest cyfrą setek, 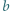 - cyfrą dziesiątek, a
- cyfrą dziesiątek, a  - cyfrą jedności, jest pierwsza. Dowieść, że
- cyfrą jedności, jest pierwsza. Dowieść, że 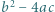 nie jest kwadratem liczby naturalnej.
nie jest kwadratem liczby naturalnej.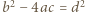 dla pewnej liczby naturalnej
dla pewnej liczby naturalnej 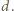 Niech
Niech 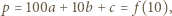 gdzie
gdzie 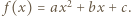 Korzystając z postaci iloczynowej, otrzymamy po przekształceniach
Korzystając z postaci iloczynowej, otrzymamy po przekształceniach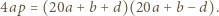
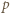 jest pierwsza, więc dzieli co najmniej jedną z liczb:
jest pierwsza, więc dzieli co najmniej jedną z liczb: 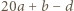 lub
lub 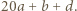 Tu mamy sprzeczność, bo są to liczby dodatnie mniejsze od
Tu mamy sprzeczność, bo są to liczby dodatnie mniejsze od 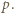
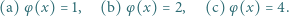
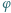 oznacza funkcję Eulera.
oznacza funkcję Eulera.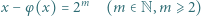
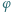 oznacza funkcję Eulera.
oznacza funkcję Eulera.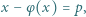
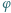 jest funkcją Eulera, a
jest funkcją Eulera, a 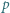 jest daną liczbą pierwszą. Wykazać, że równanie (*):
jest daną liczbą pierwszą. Wykazać, że równanie (*):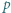 ).
).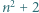 oraz
oraz 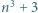 dla pewnej liczby naturalnej
dla pewnej liczby naturalnej 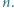
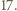
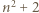 oraz
oraz 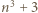 dzieli również liczbę
dzieli również liczbę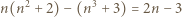
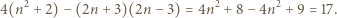
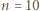 mamy
mamy 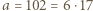 oraz
oraz 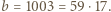
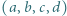 o tej własności, że każdy z iloczynów
o tej własności, że każdy z iloczynów 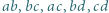 jest o 1 większy od kwadratu pewnej liczby naturalnej.
jest o 1 większy od kwadratu pewnej liczby naturalnej.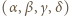 jest dowolną czwórką kolejnych liczb naturalnych nieparzystych, wówczas czwórka
jest dowolną czwórką kolejnych liczb naturalnych nieparzystych, wówczas czwórka 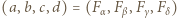 jest dobra; jak zwykle,
jest dobra; jak zwykle, 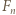 oznacza
oznacza  -tą liczbę Fibonacciego (
-tą liczbę Fibonacciego ( 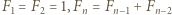 dla
dla 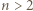 ).
).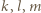 do pełnego bloku siedmiu kolejnych liczb naturalnych
do pełnego bloku siedmiu kolejnych liczb naturalnych 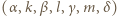 i korzystamy ze znanych tożsamości
i korzystamy ze znanych tożsamości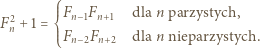
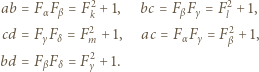
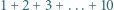 można zamienić niektóre znaki "
można zamienić niektóre znaki " 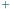 " na "
" na "  " w ten sposób, by wynik był równy
" w ten sposób, by wynik był równy 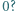
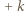 " na "
" na " 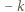 ", to wartość całego wyrażenia zmaleje o
", to wartość całego wyrażenia zmaleje o 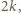 więc nie zmieni się jego parzystość. Początkowa suma jest nieparzysta, więc niemożliwe jest osiągnięcie wartości parzystej.
więc nie zmieni się jego parzystość. Początkowa suma jest nieparzysta, więc niemożliwe jest osiągnięcie wartości parzystej.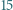 trzycyfrowych liczb pierwszych. Możemy zmazać dwie zapisane na tablicy liczby i zamiast nich zapisać wartość bezwzględną ich różnicy. Postępujemy tak aż do momentu, gdy na tablicy pozostanie jedna liczba. Czy tą liczbą może być
trzycyfrowych liczb pierwszych. Możemy zmazać dwie zapisane na tablicy liczby i zamiast nich zapisać wartość bezwzględną ich różnicy. Postępujemy tak aż do momentu, gdy na tablicy pozostanie jedna liczba. Czy tą liczbą może być 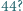
 i
i 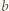 zastępujemy liczbą
zastępujemy liczbą 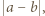 więc suma liczb na tablicy zmniejsza się o
więc suma liczb na tablicy zmniejsza się o 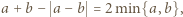 czyli nie zmienia się jej parzystość.
czyli nie zmienia się jej parzystość.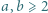 są liczbami naturalnymi, to liczby
są liczbami naturalnymi, to liczby 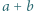 i
i 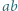 mają ten sam kolor. Dowieść, że wszystkie liczby naturalne większe od
mają ten sam kolor. Dowieść, że wszystkie liczby naturalne większe od 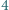 mają ten sam kolor.
mają ten sam kolor.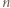 parzystych ten sam kolor mają liczby
parzystych ten sam kolor mają liczby  i
i 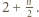 Dla
Dla 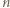 nieparzystych - liczby
nieparzystych - liczby 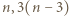 i
i 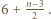
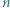 będzie liczbą naturalną. Udowodnić przez indukcję, że:
będzie liczbą naturalną. Udowodnić przez indukcję, że: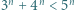 dla
dla 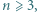 (b)
(b) 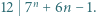
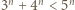 należy obustronnie pomnożyć przez 5. Otrzymamy wtedy nierówność, z której łatwo wydedukować tezę indukcyjną:
należy obustronnie pomnożyć przez 5. Otrzymamy wtedy nierówność, z której łatwo wydedukować tezę indukcyjną: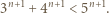
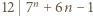 wynika, że
wynika, że 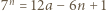 dla pewnego
dla pewnego 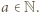 Mamy udowodnić, że
Mamy udowodnić, że 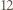 jest dzielnikiem liczby
jest dzielnikiem liczby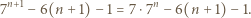
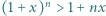 dla wszystkich liczb rzeczywistych
dla wszystkich liczb rzeczywistych 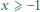 i liczb naturalnych
i liczb naturalnych 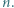
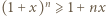 przez liczbę dodatnią
przez liczbę dodatnią 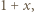 następnie wystarczy udowodnić, że
następnie wystarczy udowodnić, że 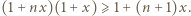
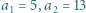 oraz
oraz 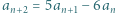 dla
dla 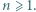 Wykazać, że
Wykazać, że 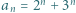 dla wszystkich naturalnych
dla wszystkich naturalnych 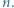
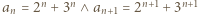 należy wykorzystać we wzorze rekurencyjnym z treści zadania w celu otrzymania tezy indukcyjnej
należy wykorzystać we wzorze rekurencyjnym z treści zadania w celu otrzymania tezy indukcyjnej 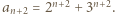
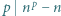 dla każdej liczby pierwszej
dla każdej liczby pierwszej 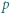 i liczby naturalnej
i liczby naturalnej 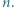
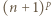 oraz fakt, że
oraz fakt, że 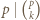 dla
dla 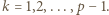
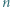 będzie liczbą naturalną. Dowieść, że istnieje
będzie liczbą naturalną. Dowieść, że istnieje  -cyfrowa wielokrotność liczby
-cyfrowa wielokrotność liczby 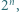 w której zapisie dziesiętnym występują tylko cyfry
w której zapisie dziesiętnym występują tylko cyfry 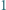 i
i 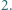
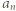 będzie poszukiwaną
będzie poszukiwaną 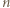 -cyfrową wielokrotnością liczby
-cyfrową wielokrotnością liczby 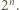 Szukaną wielokrotnością
Szukaną wielokrotnością 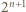 jest jedna z liczb:
jest jedna z liczb: 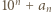 lub
lub