Klub 44M - zadania XII 2018»Zadanie 772
o zadaniu...
- Zadanie pochodzi z artykułu Klub 44M - zadania XII 2018
- Publikacja w Delcie: grudzień 2018
- Publikacja elektroniczna: 30 listopada 2018
- Artykuł źródłowy w wersji do druku [application/pdf]: (86 KB)
-
Zadanie 772 zaproponował pan Tomasz Ordowski.
Niech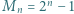 
dla 
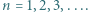Udowodnić, że następujące dwa warunki są równoważne:
- (1)
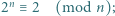
- (2)
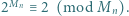
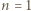oba warunki są spełnione. Dalej przyjmujemy 
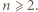Zapiszmy liczbę 
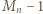jako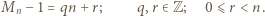
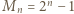mamy kongruencję 
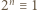(mod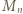 
), którą podnosimy do potęgi 
: 
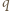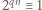(mod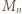 
); stąd po pomnożeniu przez 
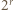(i uwzględnieniu (1)):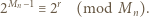
jest dzielnikiem liczby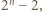 
równej 
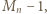czyli w równości (1) jest 
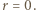Ze związku (2) dostajemy 
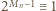(mod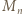 
); pomnożenie przez 2 daje warunek (ii).
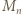) dzielimy stronami przez 2 (to dozwolone, bo 
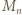jest liczbą nieparzystą), otrzymując 
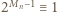(mod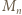 
). W połączeniu z (2) dostajemy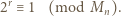
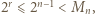więc kongruencja (3) jest równością, skąd 
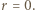To znaczy, w myśl (1), że 
dzieli liczbę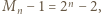 
i mamy warunek (i).