Będziemy używać oznaczenia (wychodzącego z mody): 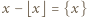 ; jest to liczba z przedziału
; jest to liczba z przedziału 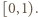 Znane (i łatwe do sprawdzenia) własności tego symbolu:
Znane (i łatwe do sprawdzenia) własności tego symbolu:
 |
(1) |
 |
(2) |
Niech 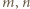 będą dodatnimi liczbami całkowitymi spełniającymi podany w zadaniu warunek. Dla
będą dodatnimi liczbami całkowitymi spełniającymi podany w zadaniu warunek. Dla 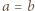 przybiera on postać
przybiera on postać
 |
(3) |
To ma zachodzić dla wszystkich liczb 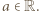 Podstawiamy
Podstawiamy 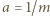 oraz
oraz 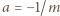 i otrzymujemy
i otrzymujemy
 |
(4) |
Oznaczając 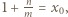 mamy więc
mamy więc
 |
(5) |
To znaczy, że dla 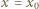 oraz dla
oraz dla 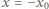 lewa strona (1) ma wartość niedodatnią. Zgodnie z własnością (1), ta wartość musi być zerem, co ma miejsce jedynie, gdy
lewa strona (1) ma wartość niedodatnią. Zgodnie z własnością (1), ta wartość musi być zerem, co ma miejsce jedynie, gdy 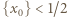 oraz
oraz 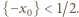 Dla tej liczby
Dla tej liczby 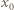 nie jest więc spełniona równość (2), co pokazuje, że
nie jest więc spełniona równość (2), co pokazuje, że 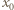 jest liczbą całkowitą, czyli że
jest liczbą całkowitą, czyli że  dzieli się przez
dzieli się przez 
Wracamy do nierówności (3) i zauważamy, że dla 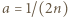 jej prawa strona jest dodatnia. Wobec tego i lewa strona musi być dodatnia, skąd
jej prawa strona jest dodatnia. Wobec tego i lewa strona musi być dodatnia, skąd 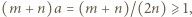 czyli
czyli 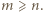 Ale
Ale  dzieli się przez
dzieli się przez  Zatem
Zatem 
Na odwrót, gdy 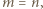 nierówność dana w zadaniu jest spełniona dla wszystkich liczb
nierówność dana w zadaniu jest spełniona dla wszystkich liczb 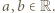 By to sprawdzić, oznaczmy
By to sprawdzić, oznaczmy 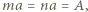
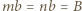 ; należy pokazać, że
; należy pokazać, że
 |
(6) |
Przy oznaczeniach 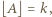
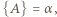
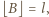
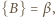 zależność (4) jest równoważna następującej:
zależność (4) jest równoważna następującej:
 |
(7) |
czyli krócej:
 |
(8) |
Jeśli choć jedna z liczb 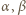 wynosi co najmniej
wynosi co najmniej 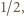 lewa strona (5) wynosi co najmniej 1 i nierówność (5) zachodzi; a jeśli
lewa strona (5) wynosi co najmniej 1 i nierówność (5) zachodzi; a jeśli 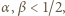 wówczas obie strony (5) są zerami.
wówczas obie strony (5) są zerami.
Ostatecznie szukane pary liczb całkowitych 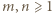 to pary równych liczb.
to pary równych liczb.
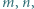 że nierówność
że nierówność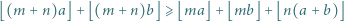
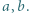

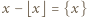 ; jest to liczba z przedziału
; jest to liczba z przedziału 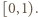 Znane (i łatwe do sprawdzenia) własności tego symbolu:
Znane (i łatwe do sprawdzenia) własności tego symbolu:

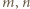 będą dodatnimi liczbami całkowitymi spełniającymi podany w zadaniu warunek. Dla
będą dodatnimi liczbami całkowitymi spełniającymi podany w zadaniu warunek. Dla 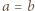 przybiera on postać
przybiera on postać
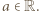 Podstawiamy
Podstawiamy 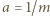 oraz
oraz 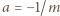 i otrzymujemy
i otrzymujemy
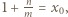 mamy więc
mamy więc
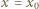 oraz dla
oraz dla 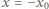 lewa strona (1) ma wartość niedodatnią. Zgodnie z własnością (1), ta wartość musi być zerem, co ma miejsce jedynie, gdy
lewa strona (1) ma wartość niedodatnią. Zgodnie z własnością (1), ta wartość musi być zerem, co ma miejsce jedynie, gdy 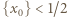 oraz
oraz 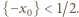 Dla tej liczby
Dla tej liczby 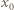 nie jest więc spełniona równość (2), co pokazuje, że
nie jest więc spełniona równość (2), co pokazuje, że 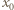 jest liczbą całkowitą, czyli że
jest liczbą całkowitą, czyli że  dzieli się przez
dzieli się przez 
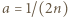 jej prawa strona jest dodatnia. Wobec tego i lewa strona musi być dodatnia, skąd
jej prawa strona jest dodatnia. Wobec tego i lewa strona musi być dodatnia, skąd 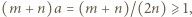 czyli
czyli 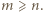 Ale
Ale  dzieli się przez
dzieli się przez  Zatem
Zatem 
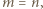 nierówność dana w zadaniu jest spełniona dla wszystkich liczb
nierówność dana w zadaniu jest spełniona dla wszystkich liczb 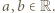 By to sprawdzić, oznaczmy
By to sprawdzić, oznaczmy 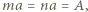
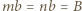 ; należy pokazać, że
; należy pokazać, że
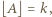
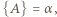
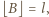
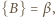 zależność (4) jest równoważna następującej:
zależność (4) jest równoważna następującej:

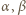 wynosi co najmniej
wynosi co najmniej 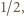 lewa strona (5) wynosi co najmniej 1 i nierówność (5) zachodzi; a jeśli
lewa strona (5) wynosi co najmniej 1 i nierówność (5) zachodzi; a jeśli 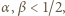 wówczas obie strony (5) są zerami.
wówczas obie strony (5) są zerami.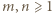 to pary równych liczb.
to pary równych liczb.