Zadanie ZM-1599
o zadaniu...
- Publikacja w Delcie: kwiecień 2019
- Publikacja elektroniczna: 31 marca 2019
Niech 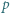 będzie nieparzystą liczbą pierwszą oraz
będzie nieparzystą liczbą pierwszą oraz 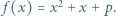 Przypuśćmy, że liczba
Przypuśćmy, że liczba 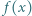 jest pierwsza dla każdej dodatniej liczby całkowitej
jest pierwsza dla każdej dodatniej liczby całkowitej  nie większej od
nie większej od 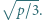 Wykazać, że liczba
Wykazać, że liczba 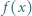 jest pierwsza dla każdej dodatniej liczby całkowitej
jest pierwsza dla każdej dodatniej liczby całkowitej 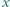 nie większej od
nie większej od 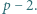

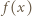 jest liczbą złożoną dla pewnego
jest liczbą złożoną dla pewnego 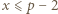 i oznaczmy przez
i oznaczmy przez  najmniejszą taką dodatnią liczbę całkowitą, że
najmniejszą taką dodatnią liczbę całkowitą, że 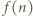 jest liczbą złożoną. Z założeń zadania wynika, że
jest liczbą złożoną. Z założeń zadania wynika, że 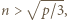 czyli
czyli 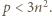
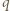 najmniejszy dzielnik pierwszy liczby
najmniejszy dzielnik pierwszy liczby 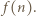 Zauważmy, że
Zauważmy, że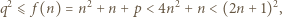
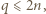 czyli istnieje liczba całkowita
czyli istnieje liczba całkowita 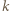 o tej własności, że
o tej własności, że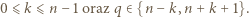
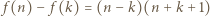
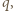 więc skoro
więc skoro 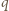 dzieli
dzieli 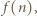 to również
to również 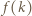 jest liczbą podzielną przez
jest liczbą podzielną przez 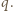 Pozostaje zauważyć, że
Pozostaje zauważyć, że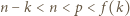
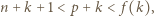
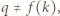 a co za tym idzie -
a co za tym idzie - 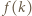 jest liczbą złożoną. Jednak
jest liczbą złożoną. Jednak 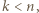 więc stoi to w sprzeczności z wyborem liczby
więc stoi to w sprzeczności z wyborem liczby