Zadanie ZM-1568
o zadaniu...
- Publikacja w Delcie: czerwiec 2018
- Publikacja elektroniczna: 22 maja 2018
Niech 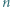 będzie dodatnią liczbą całkowitą. Wykazać, że
będzie dodatnią liczbą całkowitą. Wykazać, że 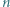 jest sumą dwóch elementów zbioru
jest sumą dwóch elementów zbioru 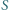 wtedy i tylko wtedy, gdy
wtedy i tylko wtedy, gdy  jest iloczynem dwóch elementów zbioru
jest iloczynem dwóch elementów zbioru 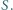

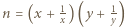 dla pewnych
dla pewnych 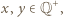 to
to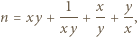
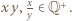 To dowodzi, że jeżeli
To dowodzi, że jeżeli 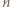 jest iloczynem dwóch elementów zbioru
jest iloczynem dwóch elementów zbioru 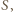 to jest również sumą dwóch elementów zbioru
to jest również sumą dwóch elementów zbioru 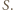
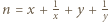 dla pewnych
dla pewnych 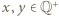 oraz niech
oraz niech 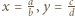 będą zapisami liczb
będą zapisami liczb 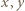 w postaci ułamków nieskracalnych, czyli
w postaci ułamków nieskracalnych, czyli 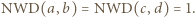 Wówczas
Wówczas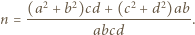
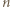 jest liczbą całkowitą, więc
jest liczbą całkowitą, więc 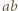 musi być dzielnikiem licznika powyższego ułamka. Stąd wniosek, że
musi być dzielnikiem licznika powyższego ułamka. Stąd wniosek, że 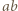 dzieli
dzieli 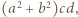 skąd wobec
skąd wobec 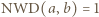 mamy, że
mamy, że 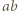 dzieli
dzieli 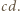 Analogicznie uzasadniamy, że
Analogicznie uzasadniamy, że 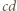 dzieli
dzieli 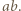 Zatem
Zatem 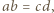 czyli
czyli 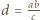 i w konsekwencji
i w konsekwencji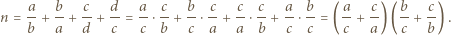
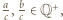 to
to 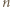 jest iloczynem dwóch elementów zbioru
jest iloczynem dwóch elementów zbioru