Zadanie ZM-1563
o zadaniu...
- Publikacja w Delcie: kwiecień 2018
- Publikacja elektroniczna: 29 marca 2018
Dana jest liczba pierwsza 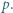 Funkcja
Funkcja 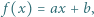 gdzie
gdzie 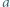 i
i 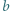 są liczbami całkowitymi, ma tę własność, że liczby
są liczbami całkowitymi, ma tę własność, że liczby

dają parami różne reszty przy dzieleniu przez 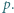 Wykazać, że
Wykazać, że 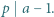

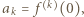 gdzie
gdzie 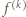 oznacza
oznacza 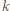 -krotne złożenie funkcji
-krotne złożenie funkcji 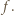 Z warunków zadania wynika, że dla pewnego
Z warunków zadania wynika, że dla pewnego 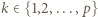 mamy
mamy 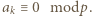 Jeżeli
Jeżeli 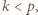 to
to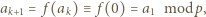
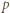 wyrazów ciągu
wyrazów ciągu 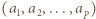 są parami różne. To oznacza, że
są parami różne. To oznacza, że 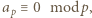 czyli
czyli 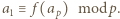
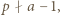 czyli
czyli 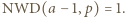 Wówczas istnieją takie liczby całkowite
Wówczas istnieją takie liczby całkowite 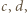 że
że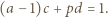
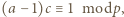 czyli
czyli 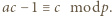 Z warunków zadania wynika, że dla pewnego
Z warunków zadania wynika, że dla pewnego 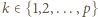 mamy
mamy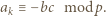
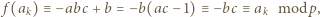
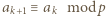 (gdzie w razie potrzeby przyjmujemy
(gdzie w razie potrzeby przyjmujemy 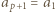 ). To stoi w sprzeczności z założeniem, że reszty z dzielenia przez
). To stoi w sprzeczności z założeniem, że reszty z dzielenia przez 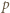 wyrazów ciągu
wyrazów ciągu 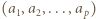 są parami różne.
są parami różne.