W jednym punkcie»Zadanie 4
o zadaniu...
- Zadanie pochodzi z artykułu W jednym punkcie
- Publikacja w Delcie: maj 2016
- Publikacja elektroniczna: 1 maja 2016
- Artykuł źródłowy w wersji do druku [application/pdf]: (81 KB)
Wszystkie kąty wewnętrzne pięciokąta 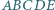 są równe. Symetralne odcinków
są równe. Symetralne odcinków 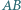 i
i  przecinają się w punkcie
przecinają się w punkcie 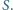 Wykaż, że proste
Wykaż, że proste 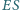 i
i 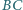 są prostopadłe.
są prostopadłe.
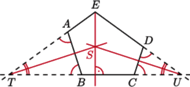
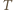 i
i 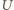 będą punktami przecięcia prostej
będą punktami przecięcia prostej 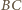 odpowiednio z prostymi
odpowiednio z prostymi 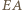 i
i 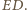 Wobec równości kątów, trójkąty
Wobec równości kątów, trójkąty 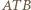 i
i 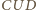 są równoramienne i podobne, a stąd
są równoramienne i podobne, a stąd 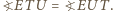 Symetralna boku
Symetralna boku 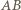 jest jednocześnie dwusieczną kąta przy wierzchołku
jest jednocześnie dwusieczną kąta przy wierzchołku 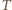 w trójkącie
w trójkącie 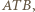 a więc także w trójkącie
a więc także w trójkącie 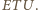 Podobnie symetralna odcinka
Podobnie symetralna odcinka 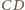 jest dwusieczną kąta
jest dwusieczną kąta 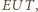 zatem
zatem 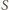 jest punktem przecięcia dwusiecznych trójkąta równoramiennego
jest punktem przecięcia dwusiecznych trójkąta równoramiennego 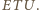 Dwusieczna
Dwusieczna 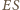 jest więc prostopadła do podstawy
jest więc prostopadła do podstawy 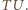
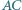 i
i 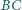 trójkąta
trójkąta 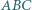 zbudowano, na zewnątrz, kwadraty
zbudowano, na zewnątrz, kwadraty 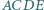 i
i 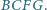 Udowodnij, że proste
Udowodnij, że proste 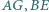 oraz wysokość
oraz wysokość 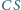 trójkąta
trójkąta 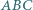 przecinają się w jednym punkcie.
przecinają się w jednym punkcie.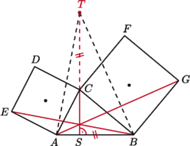
 o
o 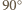 wokół środka tak, by punkt
wokół środka tak, by punkt  przeszedł na punkt
przeszedł na punkt 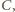 natomiast kwadrat
natomiast kwadrat 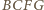 o
o 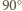 wokół swojego środka tak, by punkt
wokół swojego środka tak, by punkt 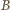 przeszedł na punkt
przeszedł na punkt 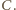 Przy obydwu tych obrotach odcinek
Przy obydwu tych obrotach odcinek 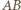 przechodzi na ten sam odcinek o końcu w punkcie
przechodzi na ten sam odcinek o końcu w punkcie 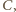 prostopadły do
prostopadły do 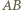 i równy
i równy 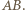 Nazwijmy drugi jego koniec
Nazwijmy drugi jego koniec 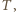 wówczas punkty
wówczas punkty 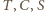 są współliniowe.
są współliniowe.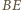 przechodzi na
przechodzi na 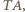 stąd
stąd 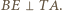 Przy drugim obrocie odcinek
Przy drugim obrocie odcinek 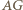 przechodzi na
przechodzi na 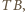 zatem
zatem 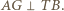 Wobec tego proste
Wobec tego proste 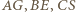 są wysokościami trójkąta
są wysokościami trójkąta 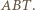
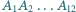 przekątne
przekątne 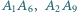 i
i 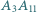 przecinają się w jednym punkcie.
przecinają się w jednym punkcie.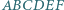 jest równa
jest równa 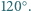 Udowodnij, że symetralne odcinków
Udowodnij, że symetralne odcinków 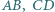 i
i 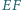 przecinają się w jednym punkcie.
przecinają się w jednym punkcie.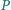 leży wewnątrz trójkąta
leży wewnątrz trójkąta 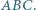 Punkty
Punkty 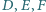 to punkty symetryczne do punktu
to punkty symetryczne do punktu 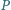 odpowiednio względem prostych
odpowiednio względem prostych 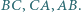 Wykaż, że jeśli trójkąt
Wykaż, że jeśli trójkąt 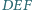 jest równoboczny, to proste
jest równoboczny, to proste 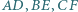 przecinają się w jednym punkcie.
przecinają się w jednym punkcie.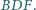
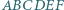 jest wpisany w okrąg. Oblicz promień tego okręgu, wiedząc, że
jest wpisany w okrąg. Oblicz promień tego okręgu, wiedząc, że 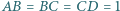 oraz
oraz 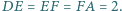
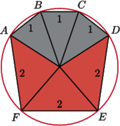
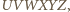 jak na rysunku.
jak na rysunku.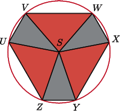
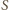 oznacza środek okręgu opisanego na sześciokącie
oznacza środek okręgu opisanego na sześciokącie 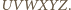 Z przystawania czworokątów
Z przystawania czworokątów 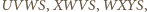
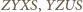 i
i 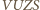 wiemy, że kąty wewnętrzne sześciokąta są przystające, mają więc po
wiemy, że kąty wewnętrzne sześciokąta są przystające, mają więc po 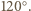 Z twierdzenia cosinusów dla trójkąta
Z twierdzenia cosinusów dla trójkąta 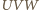 otrzymujemy
otrzymujemy 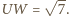 Trójkąt
Trójkąt 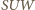 jest trójkątem równoramiennym o kącie
jest trójkątem równoramiennym o kącie 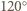 w wierzchołku
w wierzchołku 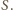 Stąd możemy obliczyć szukany promień, równy
Stąd możemy obliczyć szukany promień, równy 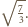
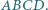 Proste zawierające dwusieczne kątów wewnętrznych
Proste zawierające dwusieczne kątów wewnętrznych 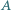 i
i 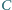 przecinają się w punkcie
przecinają się w punkcie 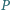 leżącym wewnątrz czworokąta
leżącym wewnątrz czworokąta 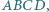 a proste zawierające dwusieczne kątów wewnętrznych
a proste zawierające dwusieczne kątów wewnętrznych 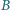 i
i 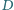 przecinają się w punkcie
przecinają się w punkcie 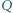 na zewnątrz czworokąta. Udowodnij, że jeżeli kąt
na zewnątrz czworokąta. Udowodnij, że jeżeli kąt 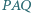 jest prosty, to również kąt
jest prosty, to również kąt 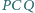 jest prosty.
jest prosty.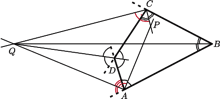
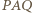 jest prosty, to
jest prosty, to 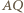 jest dwusieczną kąta przyległego do kąta
jest dwusieczną kąta przyległego do kąta 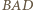 czworokąta. Z kolei aby dowieść, że kąt
czworokąta. Z kolei aby dowieść, że kąt 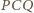 jest prosty, wystarczy wykazać, że
jest prosty, wystarczy wykazać, że 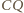 jest dwusieczną kąta przyległego do kąta
jest dwusieczną kąta przyległego do kąta 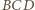 czworokąta.
czworokąta.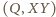 odległość punktu
odległość punktu 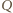 od prostej
od prostej 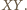 Zachodzą równości
Zachodzą równości 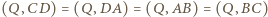 oraz
oraz 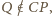 co kończy dowód.
co kończy dowód.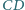 jest średnicą okręgu
jest średnicą okręgu 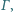 a cięciwa
a cięciwa 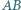 jest prostopadła do tej średnicy. Punkt
jest prostopadła do tej średnicy. Punkt 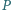 należy do krótszego łuku
należy do krótszego łuku 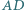 okręgu
okręgu 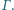 Proste
Proste 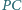 i
i 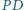 przecinają prostą
przecinają prostą 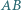 odpowiednio w punktach
odpowiednio w punktach 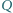 i
i 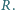 Wykaż, że
Wykaż, że 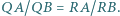
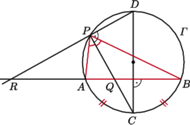
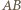 do średnicy
do średnicy 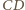 wynika, że krótsze łuki
wynika, że krótsze łuki 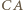 i
i 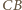 są równe, a więc półprosta
są równe, a więc półprosta 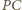 jest dwusieczną kąta wpisanego
jest dwusieczną kąta wpisanego 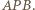 Kąt
Kąt 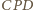 jest wpisany w okrąg i oparty na średnicy, zatem
jest wpisany w okrąg i oparty na średnicy, zatem 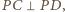 czyli półprosta
czyli półprosta 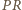 jest z kolei dwusieczną kąta zewnętrznego przy wierzchołku
jest z kolei dwusieczną kąta zewnętrznego przy wierzchołku 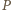 trójkąta
trójkąta 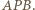 Z twierdzenia o dwusiecznej
Z twierdzenia o dwusiecznej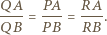
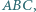 w którym kąt przy wierzchołku
w którym kąt przy wierzchołku 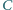 jest prosty. Punkt
jest prosty. Punkt 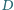 jest spodkiem wysokości opuszczonej z wierzchołka
jest spodkiem wysokości opuszczonej z wierzchołka 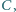 a okrąg wpisany w dany trójkąt jest styczny do boków
a okrąg wpisany w dany trójkąt jest styczny do boków 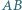 i
i 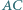 odpowiednio w punktach
odpowiednio w punktach 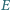 i
i 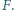 Wykaż, że ortocentrum trójkąta
Wykaż, że ortocentrum trójkąta 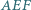 jest środkiem okręgu wpisanego w trójkąt
jest środkiem okręgu wpisanego w trójkąt 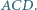
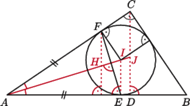
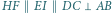
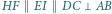
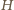 ortocentrum trójkąta
ortocentrum trójkąta 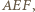 przez
przez 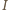 środek okręgu wpisanego w trójkąt
środek okręgu wpisanego w trójkąt 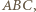 a przez
a przez 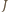 punkt przecięcia prostych
punkt przecięcia prostych 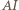 i
i 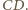 Ponieważ
Ponieważ 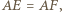 więc półprosta
więc półprosta 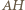 jest dwusieczną kąta
jest dwusieczną kąta 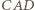 i do zakończenia dowodu wystarczy wykazać, że półprosta
i do zakończenia dowodu wystarczy wykazać, że półprosta 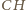 jest dwusieczną kąta
jest dwusieczną kąta 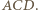
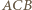 jest prosty, więc punkty
jest prosty, więc punkty 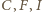 i punkt styczności okręgu wpisanego w trójkąt
i punkt styczności okręgu wpisanego w trójkąt 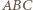 z bokiem
z bokiem 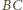 tworzą kwadrat. Stąd
tworzą kwadrat. Stąd 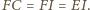
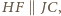 równości odcinków, twierdzenia Talesa dla
równości odcinków, twierdzenia Talesa dla 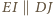 i twierdzenia o dwusiecznej, uzyskujemy
i twierdzenia o dwusiecznej, uzyskujemy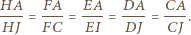
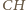 jest dwusieczną kąta
jest dwusieczną kąta 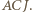
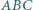 punkty
punkty 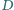 i
i 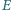 są spodkami dwusiecznych kątów wewnętrznych przy wierzchołkach
są spodkami dwusiecznych kątów wewnętrznych przy wierzchołkach 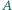 i
i 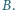 Punkt
Punkt 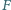 jest spodkiem dwusiecznej zewnętrznej kąta przy wierzchołku
jest spodkiem dwusiecznej zewnętrznej kąta przy wierzchołku 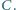 Wykaż, że punkty
Wykaż, że punkty 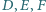 są współliniowe.
są współliniowe.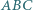 wpisany jest okrąg o promieniu
wpisany jest okrąg o promieniu 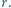 Proste styczne do okręgu i równoległe do boków trójkąta odcinają od niego trzy trójkąty. Wykaż, że suma promieni okręgów wpisanych w te trzy trójkąty jest równa
Proste styczne do okręgu i równoległe do boków trójkąta odcinają od niego trzy trójkąty. Wykaż, że suma promieni okręgów wpisanych w te trzy trójkąty jest równa 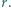

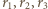 oznaczają odpowiednio promienie okręgów wpisanych w trójkąty
oznaczają odpowiednio promienie okręgów wpisanych w trójkąty 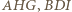 i
i 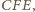 a
a 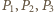 - obwody tych trójkątów. Ponadto niech
- obwody tych trójkątów. Ponadto niech 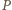 oznacza obwód trójkąta
oznacza obwód trójkąta 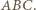
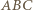 oraz punktów
oraz punktów 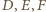 ) otrzymujemy
) otrzymujemy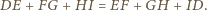
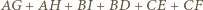
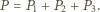
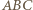 wynika, że dla
wynika, że dla 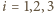 zachodzi równość
zachodzi równość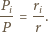
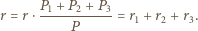
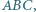 w którym
w którym 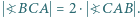 Odcinek
Odcinek 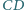 (o końcu
(o końcu 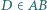 ) jest dwusieczną kąta
) jest dwusieczną kąta 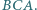 Punkt
Punkt 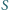 jest środkiem okręgu, stycznego zewnętrznie do okręgów opisanych na trójkątach
jest środkiem okręgu, stycznego zewnętrznie do okręgów opisanych na trójkątach 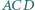 i
i 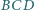 oraz stycznego do półprostej
oraz stycznego do półprostej 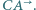 Udowodnić, że proste
Udowodnić, że proste 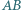 i
i 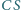 są prostopadłe.
są prostopadłe.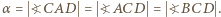 Duży okrąg o środku
Duży okrąg o środku 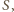 którego dotyczy zadanie, oznaczmy symbolem
którego dotyczy zadanie, oznaczmy symbolem 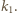 Okręgi opisane na trójkątach
Okręgi opisane na trójkątach 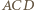 i
i 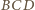 oznaczmy przez
oznaczmy przez 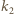 i
i 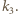 Niech
Niech 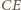 będzie cięciwą okręgu
będzie cięciwą okręgu 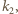 równoległą do
równoległą do 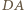 (zatem
(zatem 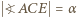 ), i niech
), i niech 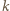 będzie okręgiem o środku
będzie okręgiem o środku 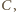 stycznym do prostej
stycznym do prostej 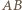 w punkcie
w punkcie 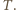 Skoro
Skoro 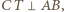 teza zadania sprowadza się do wykazania, że punkt
teza zadania sprowadza się do wykazania, że punkt 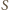 leży na prostej
leży na prostej 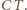
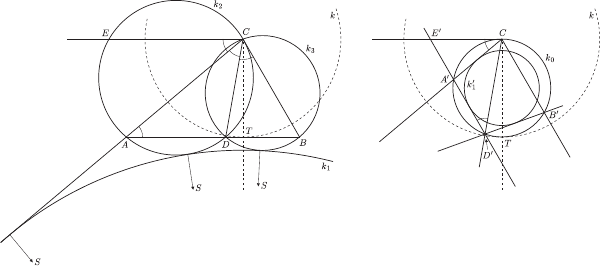
 Każda z półprostych
Każda z półprostych 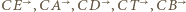 (bez punktu
(bez punktu 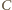 ) jest odwzorowywana na samą siebie. Prosta
) jest odwzorowywana na samą siebie. Prosta 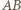 przechodzi na okrąg
przechodzi na okrąg 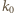 o średnicy
o średnicy 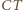 (punkt
(punkt 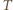 nie zmienia położenia). Obrazami punktów
nie zmienia położenia). Obrazami punktów 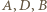 są punkty
są punkty 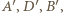 w których półproste
w których półproste 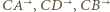 przecinają okrąg
przecinają okrąg 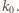 Okręgi
Okręgi 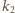 i
i 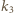 (bez punktu
(bez punktu 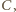 który jest środkiem inwersji) zostają przekształcone na proste
który jest środkiem inwersji) zostają przekształcone na proste 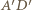 oraz
oraz 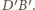 Obrazem okręgu
Obrazem okręgu 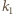 jest okrąg
jest okrąg 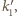 styczny do prostych
styczny do prostych 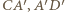 i
i 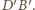
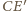 jest styczna do okręgu
jest styczna do okręgu 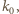 więc
więc 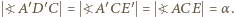
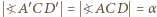 oraz
oraz 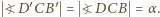 Zatem cięciwy
Zatem cięciwy 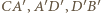 okręgu
okręgu 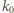 są jednakowej długości. Okrąg
są jednakowej długości. Okrąg 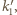 styczny do tych trzech cięciw, jest wobec tego współśrodkowy z okręgiem
styczny do tych trzech cięciw, jest wobec tego współśrodkowy z okręgiem 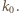 Prosta
Prosta 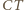 jest więc osią symetrii okręgu
jest więc osią symetrii okręgu 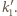
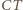 jest też osią symetrii okręgu
jest też osią symetrii okręgu 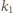 - przechodzi zatem przez jego środek, czyli punkt
- przechodzi zatem przez jego środek, czyli punkt 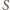 - a to właśnie mieliśmy wykazać.
- a to właśnie mieliśmy wykazać.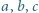 są długościami boków trójkąta, to
są długościami boków trójkąta, to
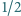 (po prawej stronie) może być zastąpiony przez liczbę większą?
(po prawej stronie) może być zastąpiony przez liczbę większą?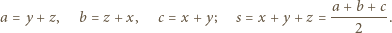
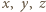 to długości fragmentów boków od wierzchołków do punktów styczności z okręgiem wpisanym. Oznaczając przez
to długości fragmentów boków od wierzchołków do punktów styczności z okręgiem wpisanym. Oznaczając przez 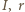 środek i promień okręgu wpisanego, mamy zgodnie z twierdzeniem Pitagorasa
środek i promień okręgu wpisanego, mamy zgodnie z twierdzeniem Pitagorasa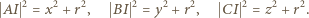
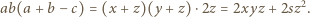
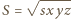 (wzór Herona) oraz
(wzór Herona) oraz 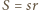 ; stąd
; stąd 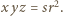 Kontynuujemy przekształcenie (1):
Kontynuujemy przekształcenie (1):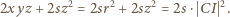
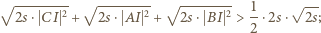
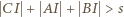
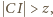
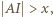
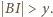
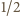 (w oryginalnej nierówności) jest optymalna.
(w oryginalnej nierówności) jest optymalna.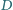 i
i 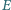 leżą odpowiednio na bokach
leżą odpowiednio na bokach 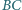 i
i 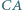 trójkąta
trójkąta 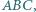 przy czym
przy czym 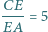 oraz
oraz 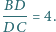 Odcinki
Odcinki 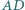 i
i 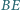 przecinają się w punkcie
przecinają się w punkcie 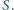 W jakim stosunku punkt
W jakim stosunku punkt 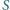 dzieli odcinek
dzieli odcinek 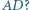
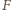 będzie takim punktem na odcinku
będzie takim punktem na odcinku 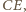 że proste
że proste 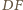 i
i 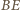 są równoległe. Wówczas z twierdzenia Talesa otrzymujemy
są równoległe. Wówczas z twierdzenia Talesa otrzymujemy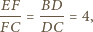
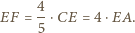
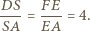
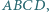 w którym boki
w którym boki 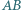 i
i 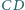 nie są równoległe. Rozważamy okrąg, przechodzący przez punkty
nie są równoległe. Rozważamy okrąg, przechodzący przez punkty 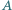 i
i 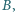 styczny do prostej
styczny do prostej 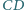 w punkcie
w punkcie 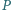 oraz okrąg, przechodzący przez punkty
oraz okrąg, przechodzący przez punkty 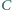 i
i 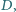 styczny do prostej
styczny do prostej 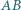 w punkcie
w punkcie 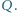 Zakładamy, że punkty
Zakładamy, że punkty 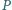 i
i 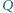 leżą na odcinkach
leżą na odcinkach 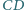 i
i 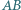 oraz że wspólna cięciwa tych okręgów przechodzi przez środek odcinka
oraz że wspólna cięciwa tych okręgów przechodzi przez środek odcinka 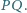 Udowodnić, że proste
Udowodnić, że proste 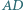 i
i 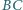 są równoległe.
są równoległe.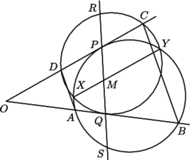
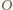 przecięcia prostych
przecięcia prostych 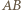 i
i 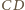 leży na półprostych
leży na półprostych 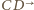 i
i 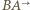 oraz że prosta
oraz że prosta 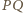 przecina okręgi
przecina okręgi 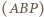 i
i 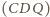 odpowiednio w punktach
odpowiednio w punktach 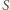 i
i 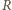 (różnych od
(różnych od 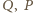 ). Wspólna cięciwa tych okręgów - nazwijmy ją
). Wspólna cięciwa tych okręgów - nazwijmy ją 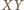 - przechodzi przez środek
- przechodzi przez środek 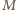 odcinka
odcinka 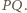 Z równości
Z równości 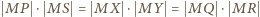 oraz
oraz 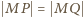 wnosimy, że
wnosimy, że 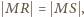 a stąd
a stąd 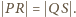
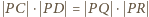 oraz
oraz 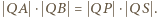 Prawe strony tych równości są równe, więc lewe też. Oznaczając odległości punktów
Prawe strony tych równości są równe, więc lewe też. Oznaczając odległości punktów 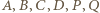 od punktu
od punktu 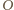 kolejno literami
kolejno literami 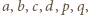 przepisujemy uzyskaną zależność w postaci
przepisujemy uzyskaną zależność w postaci 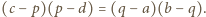 Po wymnożeniu i uwzględnieniu równości
Po wymnożeniu i uwzględnieniu równości 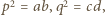 otrzymujemy związek
otrzymujemy związek 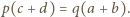 Tak więc
Tak więc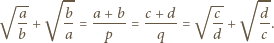
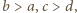 wynika stąd, że
wynika stąd, że 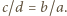 To zaś oznacza, że proste
To zaś oznacza, że proste 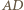 i
i 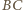 są równoległe.
są równoległe.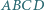 zbudowano trójkąty równoboczne
zbudowano trójkąty równoboczne 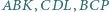 i
i 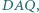 pierwsze dwa z nich na zewnątrz czworokąta, pozostałe dwa - do wewnątrz. Wykaż, że
pierwsze dwa z nich na zewnątrz czworokąta, pozostałe dwa - do wewnątrz. Wykaż, że 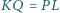 oraz
oraz 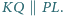

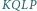
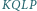
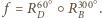 Na mocy
Na mocy 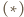 jest to przesunięcie, ponadto
jest to przesunięcie, ponadto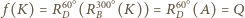
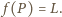 Oznacza to, że
Oznacza to, że 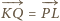 (jest to wektor przesunięcia
(jest to wektor przesunięcia 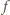 ), co kończy dowód.
), co kończy dowód.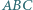 zbudowano, na zewnątrz, trójkąty równoboczne
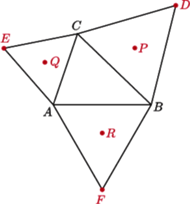
zbudowano, na zewnątrz, trójkąty równoboczne 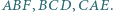 Skonstruuj trójkąt
Skonstruuj trójkąt 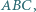 mając dane tylko punkty
mając dane tylko punkty 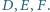
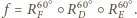 Na mocy
Na mocy 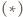 jest to obrót o
jest to obrót o 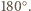 Skoro
Skoro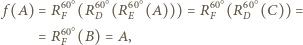
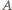 jest punktem stałym (środkiem) tego obrotu, czyli
jest punktem stałym (środkiem) tego obrotu, czyli 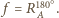
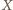 i wyznaczmy
i wyznaczmy 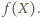 Wówczas otrzymujemy kolejno:
Wówczas otrzymujemy kolejno: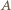 jako środek odcinka o końcach
jako środek odcinka o końcach 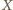 i
i 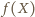 ,
, 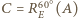 oraz
oraz 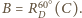
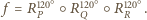 Na mocy
Na mocy 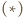 jest to przesunięcie. Ponieważ
jest to przesunięcie. Ponieważ 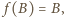 to wektor przesunięcia jest zerowy, czyli
to wektor przesunięcia jest zerowy, czyli 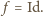 Zatem na mocy
Zatem na mocy 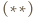 trójkąt
trójkąt 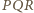 jest równoboczny.
jest równoboczny.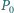 i trójkąt
i trójkąt 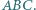 Niech
Niech 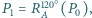
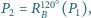
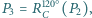
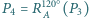 itd. Udowodnij, że jeżeli
itd. Udowodnij, że jeżeli 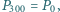 to trójkąt
to trójkąt 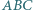 jest równoboczny.
jest równoboczny.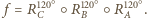 Na mocy
Na mocy 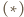 jest to przesunięcie. Z treści zadania wynika, że
jest to przesunięcie. Z treści zadania wynika, że 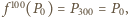 stąd wektor przesunięcia jest zerowy, czyli
stąd wektor przesunięcia jest zerowy, czyli 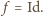 Wobec tego na mocy
Wobec tego na mocy 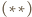 trójkąt
trójkąt 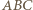 ma kąty równe
ma kąty równe 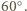
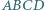 i
i 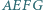 o środkach odpowiednio
o środkach odpowiednio 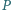 i
i 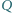 są tak samo zorientowane i mają rozłączne wnętrza. Punkty
są tak samo zorientowane i mają rozłączne wnętrza. Punkty 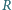 i
i 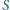 są środkami odpowiednio odcinków
są środkami odpowiednio odcinków 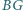 i
i 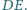 Wykaż, że czworokąt
Wykaż, że czworokąt 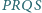 jest kwadratem.
jest kwadratem.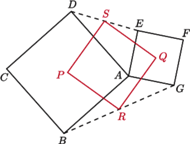
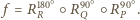 Na mocy
Na mocy 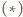 jest to przesunięcie;
jest to przesunięcie; 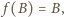 więc
więc 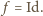 Na mocy
Na mocy 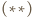 trójkąt
trójkąt 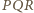 jest prostokątny i
jest prostokątny i 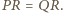 Tak samo dowodzimy, że trójkąt
Tak samo dowodzimy, że trójkąt 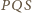 jest drugą połową kwadratu
jest drugą połową kwadratu 
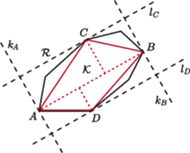
 wybierzmy te dwa, które są najdalej od siebie, i oznaczmy je przez
wybierzmy te dwa, które są najdalej od siebie, i oznaczmy je przez  i
i 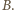 Przez te wierzchołki przeprowadźmy proste
Przez te wierzchołki przeprowadźmy proste 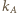 i
i 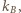 prostopadłe do odcinka
prostopadłe do odcinka 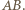 Wówczas
Wówczas 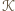 jest zawarty w pasie
jest zawarty w pasie 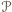 ograniczonym prostymi
ograniczonym prostymi 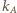 i
i 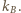 Po obu stronach prostej
Po obu stronach prostej 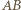 znajdźmy te wierzchołki
znajdźmy te wierzchołki 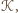 które są najdalej od tej prostej, i nazwijmy je
które są najdalej od tej prostej, i nazwijmy je 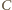 i
i 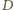 (być może któryś z nich jest wierzchołkiem
(być może któryś z nich jest wierzchołkiem 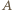 lub
lub 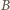 ). Przez
). Przez 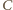 i
i 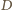 poprowadźmy proste
poprowadźmy proste 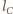 i
i 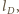 równoległe do
równoległe do 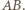 Wielokąt
Wielokąt 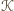 jest zawarty w pasie
jest zawarty w pasie 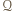 ograniczonym tymi prostymi, jest zatem zawarty w prostokącie
ograniczonym tymi prostymi, jest zatem zawarty w prostokącie 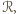 będącym przecięciem pasów
będącym przecięciem pasów 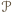 i
i 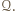 Z konstrukcji wynika, że pole prostokąta
Z konstrukcji wynika, że pole prostokąta 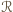 jest dwa razy większe od pola
jest dwa razy większe od pola 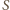 czworokąta
czworokąta 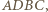 który jest zawarty w
który jest zawarty w 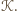 Zatem
Zatem 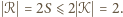
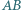 i
i 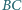 kwadratu
kwadratu 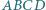 leżą (odpowiednio) takie punkty
leżą (odpowiednio) takie punkty 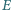 i
i 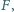 zaś wewnątrz tego kwadratu znajduje się taki punkt
zaś wewnątrz tego kwadratu znajduje się taki punkt 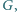 że
że 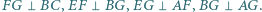 Sporządzony odręcznie rysunek sugeruje, że trapez
Sporządzony odręcznie rysunek sugeruje, że trapez  pokrywa około 40% powierzchni kwadratu
pokrywa około 40% powierzchni kwadratu  Czy jest to równość dokładna?
Czy jest to równość dokładna?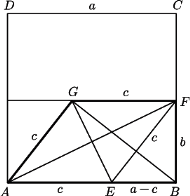
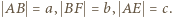 Z podanych warunków wynika, że czworokąt
Z podanych warunków wynika, że czworokąt 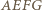 jest równoległobokiem o przekątnych prostopadłych, czyli rombem. Trójkąty
jest równoległobokiem o przekątnych prostopadłych, czyli rombem. Trójkąty 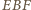 i
i 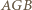 są podobne. Stąd
są podobne. Stąd 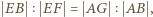 czyli
czyli 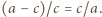 Z tego równania wyznaczamy
Z tego równania wyznaczamy 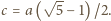 Z trójkąta prostokątnego
Z trójkąta prostokątnego 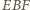 dostajemy
dostajemy 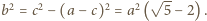 Pole trapezu
Pole trapezu 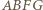 wynosi
wynosi 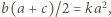 gdzie
gdzie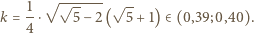
 punkty
punkty 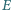 i
i 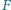 są środkami boków
są środkami boków 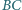 i
i 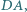 ponadto
ponadto 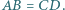 Wykaż, że prosta
Wykaż, że prosta 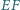 tworzy z prostymi
tworzy z prostymi 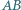 i
i 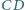 równe kąty.
równe kąty.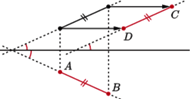
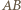 na
na 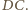 Na mocy
Na mocy 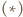 jej osią jest prosta
jej osią jest prosta 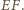 Prosta
Prosta 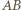 i jej obraz (prosta równoległa do
i jej obraz (prosta równoległa do 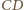 ) tworzą z osią symetrii równe kąty, co kończy dowód.
) tworzą z osią symetrii równe kąty, co kończy dowód.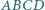 i
i 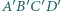 są przeciwnie zorientowane. Udowodnij, że środki odcinków
są przeciwnie zorientowane. Udowodnij, że środki odcinków 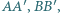
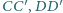 są współliniowe.
są współliniowe.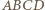 na
na 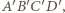 a następnie wykorzystać uwagę (*).
a następnie wykorzystać uwagę (*).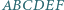 zachodzą równości
zachodzą równości 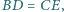
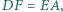
 Wykaż, że symetralne boków
Wykaż, że symetralne boków  przecinają się w jednym punkcie.
przecinają się w jednym punkcie.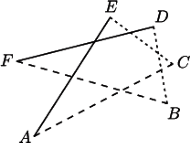
 i
i  są przystające i tak samo zorientowane, istnieje więc izometria zachowująca orientację, która przeprowadza jeden z nich na drugi. Odcinki
są przystające i tak samo zorientowane, istnieje więc izometria zachowująca orientację, która przeprowadza jeden z nich na drugi. Odcinki 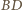 i
i 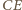 przecinają się, jako przekątne czworokąta wypukłego
przecinają się, jako przekątne czworokąta wypukłego 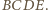 Stąd rozważana izometria jest obrotem; oznaczmy jego środek przez
Stąd rozważana izometria jest obrotem; oznaczmy jego środek przez 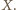
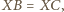 czyli punkt
czyli punkt 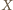 leży na symetralnej odcinka
leży na symetralnej odcinka 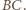 Analogicznie leży też na symetralnych
Analogicznie leży też na symetralnych 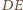 i
i 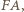 co kończy dowód.
co kończy dowód.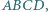 że
że 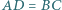 oraz boki
oraz boki 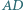 i
i 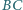 nie są równoległe. Zmienne punkty
nie są równoległe. Zmienne punkty 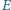 i
i 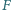 należą odpowiednio do boków
należą odpowiednio do boków 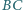 i
i 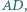 przy czym
przy czym 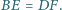 Proste
Proste 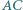 i
i 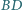 przecinają się w punkcie
przecinają się w punkcie 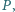 proste
proste 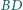 i
i 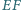 w punkcie
w punkcie 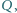 a proste
a proste 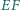 i
i 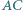 - w punkcie
- w punkcie 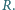 Wykaż, że okręgi opisane na trójkątach
Wykaż, że okręgi opisane na trójkątach 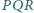 mają wspólny punkt różny od
mają wspólny punkt różny od 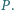
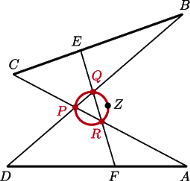
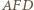 na
na 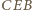 ; oznaczmy jego środek przez
; oznaczmy jego środek przez 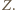 Podobnie jak w rozwiązaniu zadania 3, punkt
Podobnie jak w rozwiązaniu zadania 3, punkt 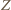 należy do symetralnych odcinków
należy do symetralnych odcinków 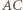 i
i 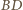 (a więc nie zależy od wyboru punktów
(a więc nie zależy od wyboru punktów 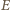 i
i 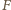 ) oraz do symetralnej
) oraz do symetralnej 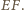 Stąd rzutami punktu
Stąd rzutami punktu 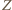 na odcinki
na odcinki 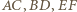 są ich środki.
są ich środki.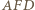 na
na 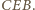 Na mocy (*), środki odcinków
Na mocy (*), środki odcinków 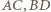 i
i 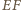 są wówczas współliniowe. Wykazaliśmy, że są to rzuty punktu
są wówczas współliniowe. Wykazaliśmy, że są to rzuty punktu 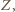 więc korzystając z twierdzenia o prostej Simsona uzyskujemy wniosek, iż stały punkt
więc korzystając z twierdzenia o prostej Simsona uzyskujemy wniosek, iż stały punkt 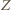 leży na każdym z okręgów opisanych na zmiennych trójkątach
leży na każdym z okręgów opisanych na zmiennych trójkątach 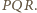
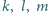 przecinają się w jednym punkcie
przecinają się w jednym punkcie 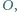 a punkt
a punkt 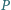 nie należy do żadnej z nich. Punkty
nie należy do żadnej z nich. Punkty 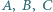 są rzutami prostokątnymi punktu
są rzutami prostokątnymi punktu 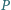 na proste
na proste 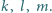 Udowodnij, że rzuty prostokątne
Udowodnij, że rzuty prostokątne 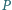 na proste
na proste 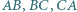 są współliniowe.
są współliniowe.
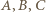 leży na okręgu o średnicy
leży na okręgu o średnicy 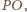 zatem punkt
zatem punkt 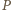 leży na okręgu opisanym na trójkącie
leży na okręgu opisanym na trójkącie 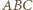 i teza wynika z twierdzenia o prostej Simsona.
i teza wynika z twierdzenia o prostej Simsona.