Zadanie ZM-1378
o zadaniu...
- Publikacja w Delcie: marzec 2013
- Publikacja elektroniczna: 01-03-2013
Punkty
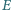 i
i
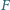 leżą odpowiednio na bokach
leżą odpowiednio na bokach
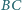 i
i
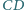 kwadratu
kwadratu
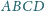 o boku 1, przy czym
o boku 1, przy czym
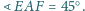 Wykaż, że
Wykaż, że
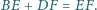
Punkty
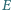 i
i
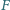 leżą odpowiednio na bokach
leżą odpowiednio na bokach
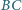 i
i
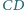 kwadratu
kwadratu
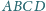 o boku 1, przy czym obwód
trójkąta
o boku 1, przy czym obwód
trójkąta
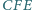 równy jest 2. Wyznacz miarę kąta
równy jest 2. Wyznacz miarę kąta
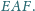
Punkty
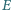 i
i
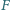 leżą odpowiednio na bokach
leżą odpowiednio na bokach
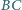 i
i
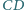 kwadratu
kwadratu
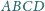 o boku 1, przy czym
o boku 1, przy czym
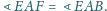 Wykaż, że
Wykaż, że
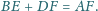
Punkty
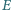 i
i
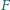 leżą odpowiednio na bokach
leżą odpowiednio na bokach
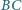 i
i
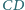 kwadratu
kwadratu
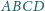 o boku 1, przy czym
o boku 1, przy czym
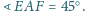 Oblicz wysokość trójkąta
Oblicz wysokość trójkąta
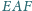 poprowadzoną
z wierzchołka
poprowadzoną
z wierzchołka
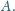
Punkty
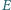 i
i
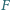 leżą odpowiednio na bokach
leżą odpowiednio na bokach
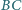 i
i
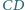 kwadratu
kwadratu
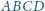 o boku 1, przy czym
o boku 1, przy czym
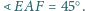 Proste
Proste
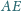 i
i
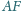 przecinają przekątną
przecinają przekątną
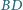 odpowiednio w punktach
odpowiednio w punktach
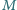 i
i
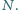 Proste
Proste
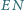 i
i
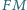 przecinają się w punkcie
przecinają się w punkcie
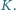 Wykaż, że proste
Wykaż, że proste
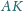 i
i
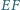 są prostopadłe.
są prostopadłe.
Punkty
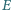 i
i
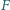 leżą odpowiednio na bokach
leżą odpowiednio na bokach
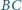 i
i
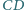 kwadratu
kwadratu
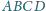 o boku 1, przy czym prosta
o boku 1, przy czym prosta
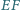 jest styczna do okręgu o środku
jest styczna do okręgu o środku
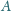 i promieniu 1. Proste
i promieniu 1. Proste
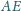 i
i
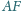 przecinają przekątną
przecinają przekątną
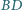 odpowiednio w punktach
odpowiednio w punktach
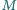 i
i
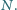 Udowodnij, że punkty
Udowodnij, że punkty
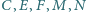 leżą na
jednym okręgu.
leżą na
jednym okręgu.
Punkty
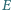 i
i
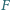 leżą odpowiednio na bokach
leżą odpowiednio na bokach
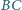 i
i
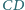 kwadratu
kwadratu
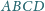 o boku 1, przy czym
o boku 1, przy czym
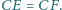 Punkt
Punkt
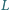 to rzut punktu
to rzut punktu
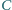 na prostą
na prostą
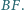 Wykaż, że
Wykaż, że
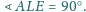
Punkt
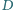 leży na boku
leży na boku
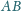 trójkąta
trójkąta
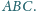 Punkt
Punkt
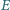 jest środkiem okręgu dopisanego, stycznego do boku
jest środkiem okręgu dopisanego, stycznego do boku
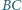 oraz
przedłużeń boków
oraz
przedłużeń boków
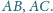 Punkt
Punkt
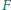 jest środkiem
okręgu wpisanego w trójkąt
jest środkiem
okręgu wpisanego w trójkąt
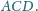 Dowieść, że jeżeli trójkąt
Dowieść, że jeżeli trójkąt
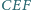 jest równoramienny, to także trójkąt
jest równoramienny, to także trójkąt
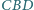 jest
równoramienny.
jest
równoramienny.
Punkty
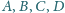 leżą, w tej właśnie kolejności, na prostej
leżą, w tej właśnie kolejności, na prostej
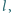 przy
czym
przy
czym
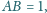
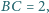
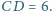 Rozstrzygnij, czy istnieje taki
punkt
Rozstrzygnij, czy istnieje taki
punkt
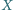 spoza prostej
spoza prostej
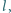 aby
aby
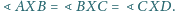
Dane są dwa okręgi rozłączne zewnętrznie. Wyznacz zbiór punktów, z których okręgi te widać pod tym samym kątem.
W czworokącie
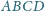 miara kąta wewnętrznego przy wierzchołku
miara kąta wewnętrznego przy wierzchołku
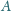 jest większa od
jest większa od
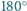 oraz zachodzi równość
oraz zachodzi równość
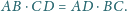 Punkt
Punkt
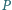 jest symetryczny do punktu
jest symetryczny do punktu
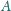 względem prostej
względem prostej
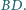 Udowodnij, że
Udowodnij, że
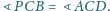
Dany jest prostokąt
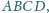 w którym
w którym
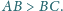 Na boku
Na boku
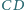 tego prostokąta skonstruuj takie punkty
tego prostokąta skonstruuj takie punkty
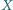 i
i
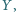 aby
aby
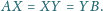
Zwardoń 2007
Rozstrzygnąć, czy istnieje taki skończony zbiór kół na płaszczyźnie o parami rozłącznych wnętrzach, że każde z danych kół jest styczne do dokładnie 5 spośród pozostałych kół.
W trójkącie prostokątnym
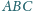 punkt
punkt
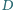 jest środkiem
przeciwprostokątnej
jest środkiem
przeciwprostokątnej
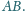 Dowieść, że prosta
Dowieść, że prosta
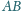 jest styczna do
okręgu, którego średnica łączy środki okręgów opisanych na trójkątach
jest styczna do
okręgu, którego średnica łączy środki okręgów opisanych na trójkątach
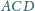 i
i
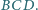
Dany jest kąt ostry
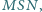 przy czym
przy czym
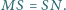 Punkt
Punkt
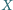 leży na krótszym łuku
leży na krótszym łuku
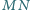 okręgu o środku
okręgu o środku
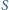 i promieniu
i promieniu
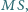 punkt
punkt
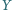 jest takim punktem odcinka
jest takim punktem odcinka
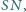 że proste
że proste
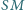 i
i
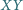 są równoległe. Znaleźć takie
położenie punktu
są równoległe. Znaleźć takie
położenie punktu
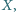 przy którym pole trójkąta
przy którym pole trójkąta
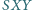 jest
największe.
jest
największe.
W czworokącie
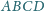 kąt
kąt
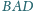 jest prosty. Wykaż, że
jest prosty. Wykaż, że

Na płaszczyźnie danych jest
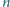 punktów, przy czym odległości między
nimi są różne dla różnych par punktów. Każdy punkt łączymy odcinkiem
z jego najbliższym sąsiadem. Czy można otrzymać w ten sposób łamaną
zamkniętą?
punktów, przy czym odległości między
nimi są różne dla różnych par punktów. Każdy punkt łączymy odcinkiem
z jego najbliższym sąsiadem. Czy można otrzymać w ten sposób łamaną
zamkniętą?
Na płaszczyźnie danych jest
 punktów białych i
punktów białych i
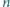 czarnych,
żadne trzy nie są współliniowe. Wykaż, że można je tak połączyć
czarnych,
żadne trzy nie są współliniowe. Wykaż, że można je tak połączyć
 odcinkami, by każdy odcinek miał końce różnych kolorów i by
żadne dwa odcinki nie miały punktów wspólnych.
odcinkami, by każdy odcinek miał końce różnych kolorów i by
żadne dwa odcinki nie miały punktów wspólnych.
Na płaszczyźnie dany jest skończony zbiór punktów, z których każde trzy są wierzchołkami trójkąta o polu mniejszym lub równym 1. Wykaż, że istnieje trójkąt o polu nie większym niż 4, zawierający wszystkie te punkty.
Na płaszczyźnie dany jest skończony zbiór punktów, z których żadne trzy nie leżą na jednej prostej. Wykaż, że można wśród nich znaleźć trzy takie, iż poprowadzony przez nie okrąg nie zawiera we wnętrzu innych punktów tego zbioru.
Każdy punkt płaszczyzny pomalowano na biało, czarno lub zielono. Udowodnić, że istnieją dwa punkty w odległości 1, które są tego samego koloru.
Znaleźć wszystkie trójkąty ostrokątne
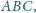 wpisane w ustalony
okrąg
wpisane w ustalony
okrąg
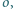 spełniające następujący warunek: środek ciężkości
spełniające następujący warunek: środek ciężkości
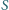 trójkąta
trójkąta
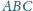 pokrywa się z ortocentrum
pokrywa się z ortocentrum
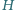 trójkąta
trójkąta
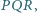 gdzie
gdzie
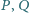 i
i
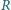 to odpowiednio punkty przecięcia
półprostych
to odpowiednio punkty przecięcia
półprostych
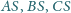 z okręgiem
z okręgiem
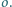
Czworokąt
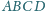 jest wpisany w okrąg. Boki
jest wpisany w okrąg. Boki
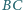 i
i
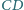 mają
jednakową długość. Na przedłużeniu odcinka
mają
jednakową długość. Na przedłużeniu odcinka
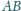 odkładamy odcinek
odkładamy odcinek
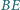 długości
długości
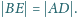 Dowieść, że
Dowieść, że
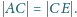
Każdy punkt płaszczyzny pomalowano na biało lub czarno. Rozstrzygnąć, czy istnieje niezdegenerowany do punktu odcinek jednokolorowy.