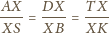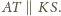I Czesko-Polsko-Słowackie Zawody Matematyczne Juniorów»Zadanie 4
o zadaniu...
- Zadanie pochodzi z artykułu I Czesko-Polsko-Słowackie Zawody Matematyczne Juniorów
- Publikacja w Delcie: sierpień 2012
- Publikacja elektroniczna: 31-07-2012
Udowodnij, że wśród dowolnych
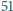 wierzchołków
wierzchołków
 -kąta
foremnego istnieją takie trzy, które są wierzchołkami trójkąta równoramiennego.
-kąta
foremnego istnieją takie trzy, które są wierzchołkami trójkąta równoramiennego.
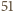 wierzchołków
wierzchołków
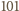 -kąta foremnego, by żadne trzy nie były wierzchołkami trójkąta
równoramiennego. Oznaczmy wówczas wierzchołki
-kąta foremnego, by żadne trzy nie były wierzchołkami trójkąta
równoramiennego. Oznaczmy wówczas wierzchołki
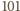 -kąta przez
-kąta przez
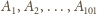 w taki sposób, by wierzchołek
w taki sposób, by wierzchołek
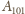 był
wybrany. Podzielmy teraz pozostałe wierzchołki na
był
wybrany. Podzielmy teraz pozostałe wierzchołki na
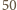 par postaci
par postaci
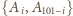 dla
dla
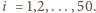 Zauważmy, że każda
z tych par tworzy podstawę trójkąta równoramiennego o wierzchołku
Zauważmy, że każda
z tych par tworzy podstawę trójkąta równoramiennego o wierzchołku
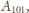 zatem z każdej pary dokładnie jeden wierzchołek musiał być
wybrany. W szczególności wybrany jest jeden z wierzchołków sąsiadujących
z
zatem z każdej pary dokładnie jeden wierzchołek musiał być
wybrany. W szczególności wybrany jest jeden z wierzchołków sąsiadujących
z
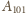 (tzn.
(tzn.
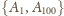 ) oraz jeden z wierzchołków odległych
o dwa miejsca od
) oraz jeden z wierzchołków odległych
o dwa miejsca od
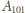 (czyli
(czyli
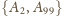 ). Nie mogą być to
jednak sąsiednie wierzchołki, bo wówczas wraz z
). Nie mogą być to
jednak sąsiednie wierzchołki, bo wówczas wraz z
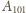 tworzyłyby
trójkąt równoramienny złożony z trzech sąsiednich wierzchołków.
Zatem, gdy z jednej strony sąsiadujący z nim wierzchołek został wybrany,
z drugiej wybrany został wierzchołek odległy od niego o dwa miejsca.
Przypuśćmy zatem bez straty ogólności, że wybrane zostały wierzchołki
tworzyłyby
trójkąt równoramienny złożony z trzech sąsiednich wierzchołków.
Zatem, gdy z jednej strony sąsiadujący z nim wierzchołek został wybrany,
z drugiej wybrany został wierzchołek odległy od niego o dwa miejsca.
Przypuśćmy zatem bez straty ogólności, że wybrane zostały wierzchołki
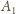 i
i
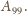 Stosując powyższe rozumowanie z wierzchołkiem
Stosując powyższe rozumowanie z wierzchołkiem
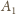 zamiast
zamiast
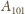 oraz z wierzchołkiem
oraz z wierzchołkiem
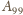 zamiast
zamiast
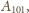 stwierdzamy, że wybrane musiały być
stwierdzamy, że wybrane musiały być
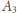 oraz
oraz
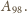 Dostajemy zatem trójkąt równoramienny
Dostajemy zatem trójkąt równoramienny
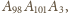 co jest
sprzeczne z założeniem. Otrzymana sprzeczność kończy rozwiązanie
zadania.
co jest
sprzeczne z założeniem. Otrzymana sprzeczność kończy rozwiązanie
zadania.
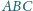 punkt
punkt
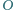 jest środkiem okręgu
opisanego, a dwusieczna kąta
jest środkiem okręgu
opisanego, a dwusieczna kąta
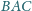 przecina bok
przecina bok
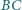 w punkcie
w punkcie
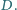 Niech
Niech
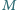 będzie takim punktem, że
będzie takim punktem, że
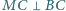 oraz
oraz
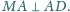 Proste
Proste
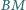 i
i
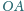 przecinają się w punkcie
przecinają się w punkcie
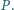 Wykazać, że okrąg o środku
Wykazać, że okrąg o środku
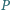 i przechodzący przez punkt
i przechodzący przez punkt
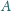 jest styczny do prostej
jest styczny do prostej
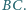
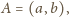
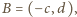
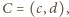
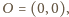
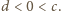 Ponieważ
trójkąt
Ponieważ
trójkąt
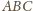 jest ostrokątny, więc
jest ostrokątny, więc
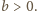 Możemy założyć, że
promień okręgu opisanego na trójkącie
Możemy założyć, że
promień okręgu opisanego na trójkącie
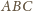 jest równy
jest równy
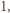 więc
więc
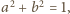
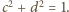 Ponieważ
Ponieważ
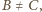 więc
więc
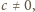 zatem
zatem
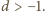 Niech
Niech
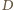 oznacza punkt wspólny boku
oznacza punkt wspólny boku
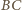 i dwusiecznej kąta
i dwusiecznej kąta
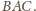 Jej równanie to
Jej równanie to
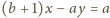 (bo
leżą na niej punkty
(bo
leżą na niej punkty
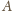 i
i
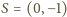 – środek łuku
– środek łuku
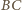 ). Wobec tego
). Wobec tego
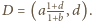 Równanie prostej
Równanie prostej
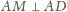 to
to
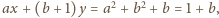 więc
więc
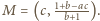 Niech
Niech
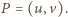 Mamy
Mamy
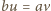 oraz
oraz
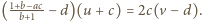 Jeśli
Jeśli
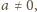 to
to
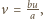 więc
więc
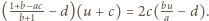 Stąd
Stąd

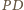 jest równoległa do prostej
jest równoległa do prostej
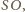 więc
trójkąty
więc
trójkąty
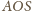 i
i
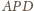 są podobne, zatem
są podobne, zatem
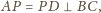 co
kończy dowód twierdzenia. Jeśli
co
kończy dowód twierdzenia. Jeśli
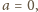 to
to
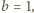 więc
więc
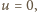 zatem
zatem
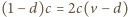 i
i
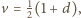 więc
więc
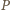 jest środkiem odcinka
jest środkiem odcinka
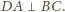 Twierdzenie zachodzi
również w tym przypadku.
Twierdzenie zachodzi
również w tym przypadku.

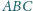 o kącie
prostym przy wierzchołku
o kącie
prostym przy wierzchołku
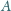 . Niech
. Niech
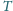 będzie środkiem
okręgu wpisanego, zaś
będzie środkiem
okręgu wpisanego, zaś
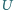 i
i
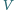 niech będą jego punktami
styczności odpowiednio z bokami
niech będą jego punktami
styczności odpowiednio z bokami
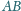 i
i
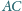 . Prosta
. Prosta
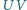 przecina w punkcie
przecina w punkcie
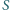 styczną do okręgu opisanego poprowadzoną
w punkcie
styczną do okręgu opisanego poprowadzoną
w punkcie
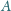 . Udowodnić, że proste
. Udowodnić, że proste
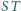 i
i
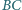 są równoległe.
są równoległe.
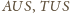 są przystające
na mocy cechy bkb (oczywiście
są przystające
na mocy cechy bkb (oczywiście
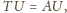 a ponadto
a ponadto
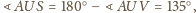
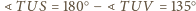 ).
).
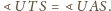 Natomiast z twierdzenia o stycznej do
okręgu i kącie wpisanym, zastosowanego do okręgu opisanego na trójkącie
Natomiast z twierdzenia o stycznej do
okręgu i kącie wpisanym, zastosowanego do okręgu opisanego na trójkącie
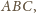 mamy
mamy
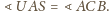 Wobec tego kąty
Wobec tego kąty
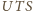 i
i
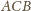 są równe, co kończy dowód.
są równe, co kończy dowód.
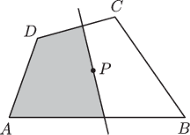
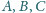 i
i
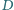 są wierzchołkami czworokąta wypukłego.
Udowodnić, że odcinki
są wierzchołkami czworokąta wypukłego.
Udowodnić, że odcinki
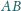 i
i
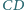 są równoległe wtedy
i tylko wtedy, gdy wewnątrz czworokąta
są równoległe wtedy
i tylko wtedy, gdy wewnątrz czworokąta
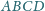 istnieje punkt
istnieje punkt
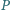 o następującej własności: każda prosta przechodząca przez
o następującej własności: każda prosta przechodząca przez
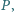 która przecina odcinki
która przecina odcinki
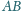 i
i
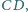 dzieli czworokąt
dzieli czworokąt
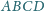 na części o równych polach.
na części o równych polach.
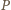 o podanej własności.
Poprowadźmy przez niego dwie proste. Jedna przecina boki
o podanej własności.
Poprowadźmy przez niego dwie proste. Jedna przecina boki
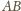 i
i
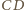 odpowiednio w punktach
odpowiednio w punktach
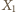 i
i
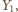 a druga –
w punktach
a druga –
w punktach
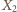 i
i
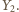 Mamy
Mamy
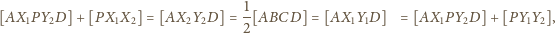
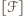 oznacza pole figury
oznacza pole figury
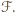 Zatem
Zatem
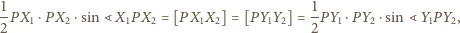
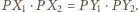 Prowadząc przez
Prowadząc przez
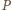 trzecią prostą,
przecinającą
trzecią prostą,
przecinającą
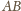 i
i
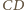 odpowiednio w punktach
odpowiednio w punktach
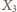 i
i
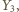 otrzymamy
otrzymamy
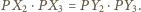 Dzieląc stronami ostatnie
dwie równości, otrzymamy
Dzieląc stronami ostatnie
dwie równości, otrzymamy
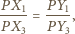
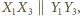 tzn.
tzn.
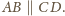
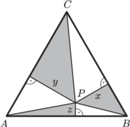
 Niech
Niech
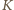 i
i
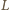 będą odpowiednio
środkami boków
będą odpowiednio
środkami boków
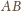 i
i
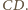 Niech
Niech
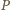 będzie środkiem
odcinka
będzie środkiem
odcinka
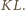
 wynika, że punkt
wynika, że punkt
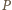 leży w jego
wnętrzu. Oczywiście
leży w jego
wnętrzu. Oczywiście
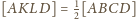 i
i
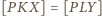 dla
dowolnej prostej przechodzącej przez
dla
dowolnej prostej przechodzącej przez
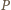 i przecinającej odcinki
i przecinającej odcinki
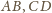 odpowiednio w punktach
odpowiednio w punktach
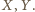 Zatem
Zatem
 ma
własność, o której mowa w treści zadania.
ma
własność, o której mowa w treści zadania.
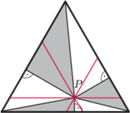
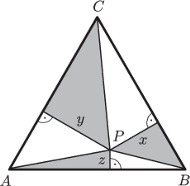
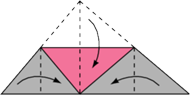
 proste równoległe do boków trójkąta.
Dzielą one trójkąt
proste równoległe do boków trójkąta.
Dzielą one trójkąt
 na trzy trójkąty równoboczne i trzy
równoległoboki. Połowa każdej z tych sześciu figur jest szara. Wobec
tego suma pól szarych trójkątów równa jest połowie pola trójkąta
na trzy trójkąty równoboczne i trzy
równoległoboki. Połowa każdej z tych sześciu figur jest szara. Wobec
tego suma pól szarych trójkątów równa jest połowie pola trójkąta
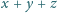 nie zależy od położenia punktu
nie zależy od położenia punktu
 suma
suma
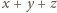 równa jest
równa jest
 ponieważ
ponieważ

 powinien leżeć punkt
powinien leżeć punkt
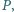 aby
z odcinków o długościach
aby
z odcinków o długościach
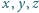 można było zbudować
trójkąt?
można było zbudować
trójkąt?
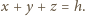 Stąd
nierówność trójkąta
Stąd
nierówność trójkąta
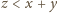 równoważna jest warunkowi
równoważna jest warunkowi
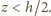 Analogicznie powinny być spełnione warunki
Analogicznie powinny być spełnione warunki
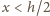 oraz
oraz
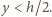 Oznacza to, że punkt
Oznacza to, że punkt
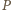 powinien leżeć wewnątrz
trójkąta utworzonego przez środki boków trójkąta
powinien leżeć wewnątrz
trójkąta utworzonego przez środki boków trójkąta
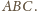
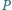 leży wewnątrz trójkąta równobocznego
leży wewnątrz trójkąta równobocznego
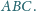 Wykaż,
że z odcinków o długościach
Wykaż,
że z odcinków o długościach
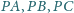 można zbudować
trójkąt.
można zbudować
trójkąt.
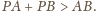 Ponadto
Ponadto
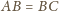 oraz
oraz
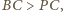 stąd
stąd
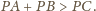 Analogicznie
Analogicznie
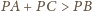 oraz
oraz
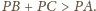
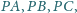 jeśli
jeśli
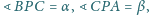
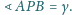
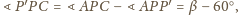 podobnie
podobnie
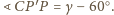 Stąd, korzystając z równości
Stąd, korzystając z równości
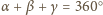 i z sumy
miar kątów trójkąta
i z sumy
miar kątów trójkąta
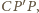 otrzymujemy
otrzymujemy
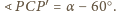
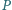 leży wewnątrz trójkąta równobocznego
leży wewnątrz trójkąta równobocznego
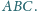 Wyznacz
pole trójkąta
Wyznacz
pole trójkąta
 jeśli
jeśli
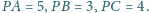
 wokół wierzchołka
wokół wierzchołka
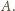 Niech
Niech
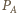 będzie
obrazem punktu
będzie
obrazem punktu
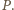 Trójkąt
Trójkąt
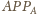 jest równoboczny. Trójkąt
jest równoboczny. Trójkąt
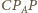 ma boki długości
ma boki długości
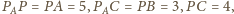 więc
jest prostokątny.
więc
jest prostokątny.
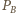 i
i
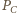 jako obrazy
jako obrazy
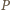 przy obrotach wokół odpowiednio wierzchołków
przy obrotach wokół odpowiednio wierzchołków
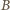 i
i
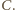 Wtedy trójkąty
Wtedy trójkąty
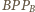 i
i
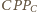 są równoboczne o bokach
odpowiednio długości 3 i 4, a trójkąty
są równoboczne o bokach
odpowiednio długości 3 i 4, a trójkąty
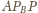 i
i
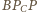 oba są
prostokątne o bokach długości 3, 4, 5.
oba są
prostokątne o bokach długości 3, 4, 5.
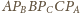 jest równe
jest równe
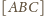 plus
„dodatki”:
plus
„dodatki”:
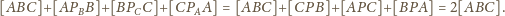
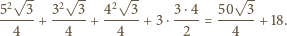
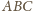 jest więc dwukrotnie mniejsze:
jest więc dwukrotnie mniejsze:
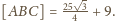
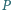 leży wewnątrz trójkąta równobocznego
leży wewnątrz trójkąta równobocznego
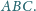 Udowodnij, że
Udowodnij, że
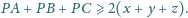
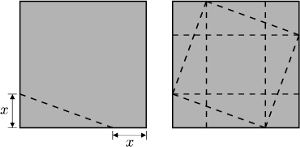
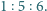 Najdłuższy bok trójkąta
to 6. Ile wynosi wysokość opuszczona na ten bok?
Najdłuższy bok trójkąta
to 6. Ile wynosi wysokość opuszczona na ten bok?
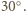 Kąt ten oparty jest na pewnym łuku okręgu, kąt środkowy oparty na
tym samym łuku to wobec tego
Kąt ten oparty jest na pewnym łuku okręgu, kąt środkowy oparty na
tym samym łuku to wobec tego
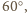 a cięciwa oparta na tym łuku jest
jednocześnie podstawą odpowiedniego trójkąta równobocznego i podwojoną
szukaną wysokością.
a cięciwa oparta na tym łuku jest
jednocześnie podstawą odpowiedniego trójkąta równobocznego i podwojoną
szukaną wysokością.
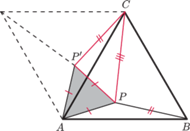
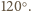 Podnosząc w przestrzeni ten punkt
nieznacznie do góry, skonstruujemy odpowiedni czworościan.
Podnosząc w przestrzeni ten punkt
nieznacznie do góry, skonstruujemy odpowiedni czworościan.
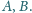 Rozważamy wszystkie
czworokąty wypukłe
Rozważamy wszystkie
czworokąty wypukłe
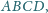 położone w ustalonej półpłaszczyźnie
o krawędzi
położone w ustalonej półpłaszczyźnie
o krawędzi
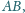 symetryczne względem prostej
symetryczne względem prostej
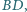 z kątem
prostym przy wierzchołku
z kątem
prostym przy wierzchołku
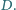 Wykazać, że istnieje punkt wspólny
wszystkich uzyskanych prostych
Wykazać, że istnieje punkt wspólny
wszystkich uzyskanych prostych
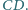
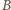 prowadzimy półprostą
prowadzimy półprostą
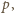 prostopadłą do
prostopadłą do
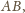 położoną w rozpatrywanej półpłaszczyźnie. Niech
położoną w rozpatrywanej półpłaszczyźnie. Niech
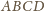 będzie jednym z rozważanych czworokątów. Trójkąt
będzie jednym z rozważanych czworokątów. Trójkąt
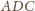 jest prostokątny, równoramienny. Stąd (i z wypukłości czworokąta
jest prostokątny, równoramienny. Stąd (i z wypukłości czworokąta
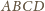 ) wynika, że punkt
) wynika, że punkt
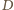 leży po tej stronie
leży po tej stronie
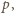 co
punkt
co
punkt
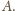 Półprosta
Półprosta
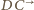 przecina więc
przecina więc
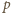 w pewnym
punkcie
w pewnym
punkcie
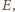 tworząc czworokąt wypukły
tworząc czworokąt wypukły
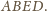 Ma on kąty proste
przy wierzchołkach
Ma on kąty proste
przy wierzchołkach
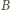 i
i
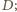 można na nim opisać okrąg.
Zatem
można na nim opisać okrąg.
Zatem
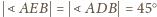 (ostatnia równość zachodzi,
bo
(ostatnia równość zachodzi,
bo
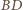 jest symetralną odcinka
jest symetralną odcinka
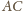 ). Stąd wniosek, że
). Stąd wniosek, że
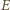 jest wierzchołkiem kwadratu, którego jednym bokiem jest odcinek
jest wierzchołkiem kwadratu, którego jednym bokiem jest odcinek
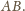 Jest to szukany punkt wspólny wszystkich możliwych prostych
Jest to szukany punkt wspólny wszystkich możliwych prostych
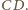
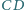 trójkąta równoramiennego
trójkąta równoramiennego
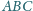 o podstawie
o podstawie
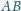 dany jest punkt
dany jest punkt
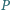 . Proste
. Proste
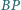 i
i
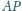 przecinają
boki
przecinają
boki
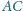 i
i
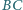 odpowiednio w punktach
odpowiednio w punktach
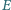 i
i
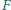 .
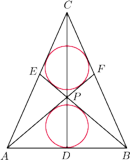
Okrąg wpisany w trójkąt
.
Okrąg wpisany w trójkąt
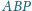 przystaje do okręgu wpisanego
w czworokąt
przystaje do okręgu wpisanego
w czworokąt
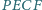 . Udowodnić, ze okręgi wpisane w trójkąty
. Udowodnić, ze okręgi wpisane w trójkąty
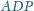 i
i
 też są przystające.
też są przystające.
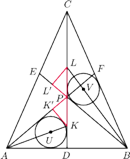
 i
i
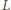 oznaczmy środki okręgów wpisanych odpowiednio
w trójkąt
oznaczmy środki okręgów wpisanych odpowiednio
w trójkąt
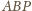 i czworokąt
i czworokąt
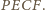
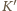 i
i
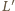 będą rzutami prostokątnymi punktów
będą rzutami prostokątnymi punktów
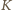 i
i
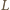 odpowiednio na
odpowiednio na
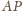 i
i
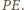 Niech wreszcie
Niech wreszcie
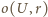 i
i
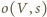 będą okręgami wpisanymi w trójkąty
będą okręgami wpisanymi w trójkąty
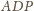 i
i
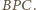 Chcemy wykazać, że
Chcemy wykazać, że
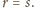
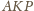 i
i
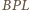 są równe, bo
podstawy
są równe, bo
podstawy
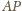 i
i
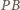 oraz odpowiednie wysokości
oraz odpowiednie wysokości
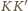 i
i
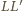 są równej długości. Skoro
są równej długości. Skoro
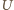 leży na
leży na
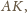 a
a
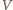 na
na
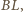 to możemy obliczyć pola tych trójkątów innym
sposobem, otrzymując
to możemy obliczyć pola tych trójkątów innym
sposobem, otrzymując
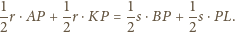
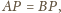 zaś
zaś
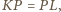 gdyż trójkąty prostokątne
gdyż trójkąty prostokątne
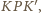
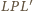 są przystające (kąty
są przystające (kąty
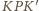 i
i
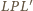 są
równe, boki
są
równe, boki
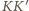 i
i
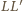 też). Zatem
też). Zatem
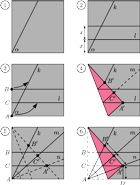
 punkt
punkt
 jest środkiem okręgu wpisanego.
Prosta
jest środkiem okręgu wpisanego.
Prosta
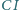 przecina bok
przecina bok
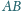 w punkcie
w punkcie
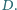 Prowadzimy
przez punkt
Prowadzimy
przez punkt
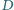 dowolną prostą, przecinającą okrąg opisany na
trójkącie
dowolną prostą, przecinającą okrąg opisany na
trójkącie
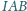 w punktach
w punktach
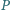 i
i
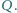 Wykazać, że prosta
Wykazać, że prosta
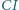 jest dwusieczną kąta
jest dwusieczną kąta
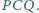

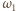 i
i
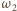 będą (odpowiednio) okręgami opisanymi
na trójkątach
będą (odpowiednio) okręgami opisanymi
na trójkątach
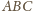 i
i
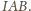 Dwusieczna
Dwusieczna
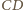 kąta
kąta
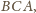 a raczej jej przedłużenie, przecina okrąg
a raczej jej przedłużenie, przecina okrąg
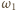 w środku
łuku
w środku
łuku
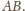 Oznaczmy ten punkt przez
Oznaczmy ten punkt przez
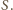 Zachodzi równość
Zachodzi równość
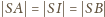 (znana, a przy tym łatwa do wykazania). Punkt
(znana, a przy tym łatwa do wykazania). Punkt
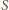 jest więc środkiem okręgu
jest więc środkiem okręgu
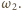 Zatem
Zatem
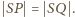
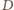 przecinają się cięciwy
przecinają się cięciwy
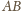 i
i
 okręgu
okręgu
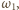 a także cięciwy
a także cięciwy
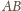 i
i
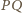 okręgu
okręgu
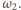 Tak
więc
Tak
więc
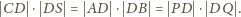
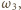 przechodzący przez punkty
przechodzący przez punkty
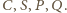 Jego cięciwy
Jego cięciwy
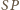 i
i
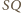 mają jednakową długość, więc wyznaczają przystające
łuki
mają jednakową długość, więc wyznaczają przystające
łuki
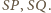 Oparte na nich kąty
Oparte na nich kąty
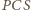 i
i
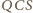 (wpisane
w okrąg
(wpisane
w okrąg
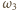 ) są równe – a to jest teza zadania.
) są równe – a to jest teza zadania.
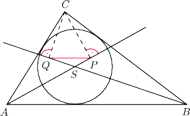
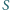 jest środkiem okręgu wpisanego w trójkąt
jest środkiem okręgu wpisanego w trójkąt
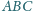 . Punkty
. Punkty
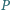 i
i
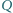 są rzutami prostopadłymi punktu
są rzutami prostopadłymi punktu
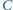 odpowiednio na
proste
odpowiednio na
proste
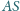 i
i
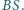 Udowodnić, że prosta
Udowodnić, że prosta
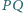 jest
równoległa do prostej
jest
równoległa do prostej
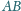 .
.
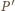 i
i
 będą punktami przecięcia prostej
będą punktami przecięcia prostej
 odpowiednio
z prostymi
odpowiednio
z prostymi
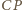 i
i
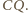
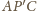 dwusieczna
dwusieczna
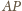 jest prostopadła do boku
jest prostopadła do boku
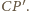 Wobec tego
Wobec tego
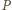 jest środkiem odcinka
jest środkiem odcinka
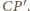 Podobnie,
Podobnie,
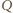 jest środkiem odcinka
jest środkiem odcinka
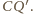 Zatem prosta
Zatem prosta
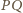 jest
równoległa do prostej
jest
równoległa do prostej
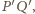 czyli do prostej
czyli do prostej
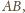 na mocy
twierdzenia odwrotnego do twierdzenia Talesa.
na mocy
twierdzenia odwrotnego do twierdzenia Talesa.

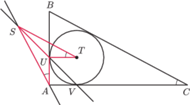
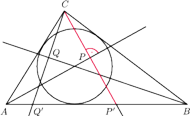
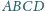 jest styczny do boków
jest styczny do boków
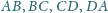 odpowiednio w punktach
odpowiednio w punktach
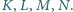 Udowodnij,
że proste
Udowodnij,
że proste
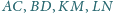 przecinają się w jednym punkcie.
przecinają się w jednym punkcie.
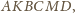 proste
proste
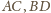 i
i
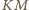 przecinają się
w jednym punkcie. Z kolei z twierdzenia Brianchona dla zdegenerowanego
sześciokąta
przecinają się
w jednym punkcie. Z kolei z twierdzenia Brianchona dla zdegenerowanego
sześciokąta
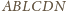 wynika, że przez punkt przecięcia prostych
wynika, że przez punkt przecięcia prostych
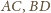 przechodzi także prosta
przechodzi także prosta
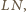 co kończy dowód.
co kończy dowód.
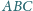 jest styczny do boków
jest styczny do boków
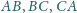 odpowiednio w punktach
odpowiednio w punktach
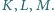 Wykaż, że
proste
Wykaż, że
proste
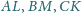 przecinają się w jednym punkcie.
przecinają się w jednym punkcie.
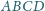 jest opisany na okręgu o środku
jest opisany na okręgu o środku
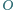 i promieniu 1.
Przekątne tego trapezu przecinają się w punkcie
i promieniu 1.
Przekątne tego trapezu przecinają się w punkcie
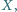 przy czym
przy czym
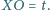 Wyznacz stosunek
Wyznacz stosunek
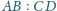 długości podstaw tego
trapezu, jeśli
długości podstaw tego
trapezu, jeśli
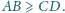
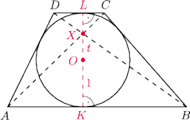
 odpowiednio punkty styczności podstaw
odpowiednio punkty styczności podstaw
 z okręgiem. Wtedy
z okręgiem. Wtedy
 oraz
oraz
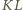 przechodzi
przez punkt
przechodzi
przez punkt
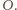 Z twierdzenia Brianchona dla czworokąta,
Z twierdzenia Brianchona dla czworokąta,
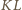 przechodzi też przez punkt
przechodzi też przez punkt
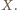 Trójkąty
Trójkąty
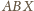 i
i
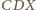 są podobne, więc
są podobne, więc
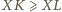 oraz
oraz
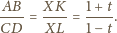
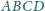 jest styczny do boku
jest styczny do boku
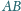 w punkcie
w punkcie
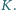 Styczna do tego okręgu przecina boki
Styczna do tego okręgu przecina boki
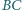 i
i
 odpowiednio
w punktach
odpowiednio
w punktach
 i
i
 Wykaż, że
Wykaż, że

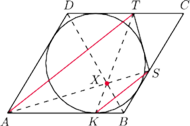
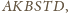 proste
proste
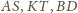 przecinają się w jednym punkcie
przecinają się w jednym punkcie
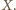 Z twierdzenia
Talesa ponieważ
Z twierdzenia
Talesa ponieważ
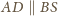 oraz
oraz
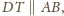 więc
więc