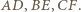Zadanie ZM-1534
o zadaniu...
- Publikacja w Delcie: lipiec 2017
- Publikacja elektroniczna: 30 czerwca 2017
Czy na płaszczyźnie można wskazać taki skończony zbiór 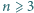 punktów
punktów 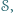 że dla każdego
że dla każdego 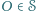 istnieją
istnieją 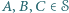 o tej własności, że punkt
o tej własności, że punkt 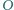 jest środkiem okręgu opisanego na trójkącie
jest środkiem okręgu opisanego na trójkącie 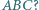
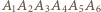 będzie sześciokątem foremnym o boku 1, a
będzie sześciokątem foremnym o boku 1, a 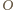 będzie środkiem okręgu opisanego na tym sześciokącie. Wówczas
będzie środkiem okręgu opisanego na tym sześciokącie. Wówczas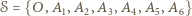
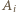 jest środkiem okręgu opisanego na trójkącie
jest środkiem okręgu opisanego na trójkącie 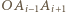 dla
dla 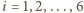 (przyjmujemy
(przyjmujemy 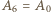 i
i 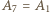 ).
).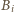 środek okręgu opisanego na trójkącie
środek okręgu opisanego na trójkącie 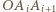 dla
dla 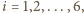 a przez
a przez 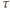 - dowolną translację o wektor długości większej od
- dowolną translację o wektor długości większej od 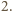 Wówczas, jeżeli
Wówczas, jeżeli 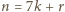 dla
dla 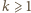 oraz
oraz 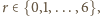 to zbiór
to zbiór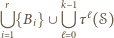
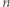 elementów i spełnia warunki zadania (
elementów i spełnia warunki zadania ( 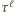 oznacza
oznacza 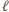 -krotne złożenie
-krotne złożenie  ).
).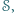 że dla każdych trzech niewspółliniowych punktów
że dla każdych trzech niewspółliniowych punktów 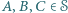 środek okręgu opisanego na trójkącie
środek okręgu opisanego na trójkącie 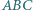 również należy do
również należy do 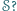
 istnieje. Spośród wszystkich odcinków o obu końcach w zbiorze
istnieje. Spośród wszystkich odcinków o obu końcach w zbiorze 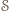 wybierzmy taki, który ma najmniejszą długość i nazwijmy go
wybierzmy taki, który ma najmniejszą długość i nazwijmy go 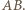 Ponieważ zbiór
Ponieważ zbiór 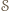 nie jest zawarty w prostej, więc poza prostą
nie jest zawarty w prostej, więc poza prostą 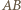 jest co najmniej jeden punkt zbioru
jest co najmniej jeden punkt zbioru 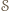 - spośród wszystkich takich punktów wybierzmy taki punkt
- spośród wszystkich takich punktów wybierzmy taki punkt 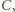 dla którego miara kąta
dla którego miara kąta 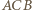 jest największa.
jest największa.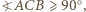 to
to 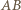 jest najdłuższym bokiem trójkąta
jest najdłuższym bokiem trójkąta 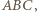 co przeczy wyborowi odcinka
co przeczy wyborowi odcinka 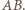 Z kolei jeżeli
Z kolei jeżeli 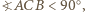 to środek
to środek 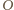 okręgu opisanego na trójkącie
okręgu opisanego na trójkącie 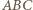 należy do
należy do 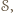 przy czym
przy czym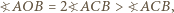
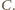 Uzyskana sprzeczność oznacza, że nie istnieje zbiór
Uzyskana sprzeczność oznacza, że nie istnieje zbiór 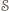 o zadanych własnościach.
o zadanych własnościach.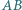 jest najkrótszym bokiem trójkąta
jest najkrótszym bokiem trójkąta 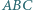 opisanego na okręgu o środku w punkcie
opisanego na okręgu o środku w punkcie 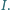 Na bokach
Na bokach 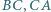 znajdują się odpowiednio takie punkty
znajdują się odpowiednio takie punkty 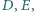 że
że 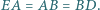 Odcinki
Odcinki 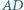 i
i 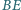 przecinają się w punkcie
przecinają się w punkcie 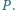 Wykazać, że proste
Wykazać, że proste 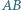 i
i  są prostopadłe.
są prostopadłe.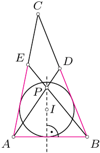
 jako dwusieczna kąta między ramionami trójkąta równoramiennego
jako dwusieczna kąta między ramionami trójkąta równoramiennego  jest prostopadła do podstawy
jest prostopadła do podstawy 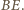 Podobnie prosta
Podobnie prosta 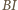 jest prostopadła do prostej
jest prostopadła do prostej 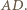 Wobec tego punkt
Wobec tego punkt 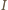 jest ortocentrum trójkąta
jest ortocentrum trójkąta 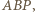 a zatem
a zatem 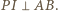

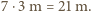 Stąd na mocy twierdzenia Pitagorasa długość winorośli to 29 m.
Stąd na mocy twierdzenia Pitagorasa długość winorośli to 29 m. jest wpisany w trójkąt
jest wpisany w trójkąt 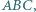 w którym
w którym 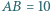 i
i 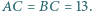 Okręgi
Okręgi 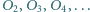 są styczne do boków
są styczne do boków 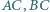 oraz dla każdego
oraz dla każdego 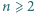 okrąg
okrąg 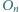 jest styczny zewnętrznie do okręgów
jest styczny zewnętrznie do okręgów 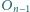 i
i 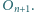 Wyznacz sumę obwodów wszystkich okręgów
Wyznacz sumę obwodów wszystkich okręgów 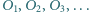
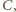 która z kolei z twierdzenia Pitagorasa ma długość 12. Okrąg o średnicy
która z kolei z twierdzenia Pitagorasa ma długość 12. Okrąg o średnicy 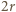 ma obwód
ma obwód 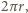 zatem szukana suma obwodów wszystkich okręgów to
zatem szukana suma obwodów wszystkich okręgów to 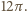
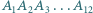 o środku
o środku 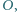 przy czym
przy czym 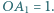 Punkt
Punkt 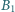 jest rzutem
jest rzutem 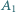 na odcinek
na odcinek 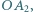 punkt
punkt 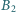 jest rzutem
jest rzutem 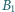 na
na 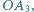 punkt
punkt 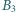 jest rzutem
jest rzutem 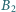 na
na 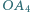 itd. Wyznacz długość łamanej
itd. Wyznacz długość łamanej 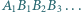

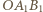 oraz
oraz 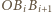 mają kąty po
mają kąty po 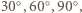 gdyż każdy z nich z założenia jest prostokątny i ma kąt
gdyż każdy z nich z założenia jest prostokątny i ma kąt 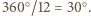 Można wobec tego ułożyć je w sposób przedstawiony na rysunku. Kąt pomiędzy sąsiadującymi teraz odcinkami rozważanej łamanej jest wówczas równy
Można wobec tego ułożyć je w sposób przedstawiony na rysunku. Kąt pomiędzy sąsiadującymi teraz odcinkami rozważanej łamanej jest wówczas równy 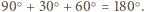
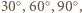 przy czym jedna jego przyprostokątna ma długość 1, a suma pozostałych dwóch boków to szukana długość łamanej. Jest ona wobec tego równa
przy czym jedna jego przyprostokątna ma długość 1, a suma pozostałych dwóch boków to szukana długość łamanej. Jest ona wobec tego równa 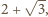 gdyż trójkąt ten jest połową trójkąta równobocznego o boku 2.
gdyż trójkąt ten jest połową trójkąta równobocznego o boku 2.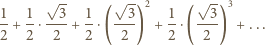
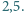 Wykaż, że obwód tego czworokąta jest większy od 7.
Wykaż, że obwód tego czworokąta jest większy od 7.
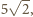 co z kolei jest większe od 7.
co z kolei jest większe od 7.
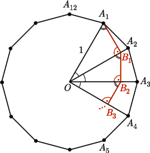
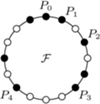
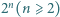 znajdują się punkty
znajdują się punkty 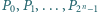 będące wierzchołkami
będące wierzchołkami 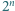 -kąta foremnego, oznaczone w taki sposób, że długość łuku
-kąta foremnego, oznaczone w taki sposób, że długość łuku 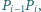 mierzonego zgodnie z ruchem wskazówek zegara, jest równa
mierzonego zgodnie z ruchem wskazówek zegara, jest równa 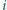 dla każdego
dla każdego 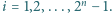 Niech
Niech
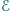 i
i 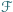 są przystające (jako podzbiory płaszczyzny).
są przystające (jako podzbiory płaszczyzny).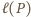 będzie długością łuku (mierzoną zgodnie z ruchem wskazówek zegara) łączącego
będzie długością łuku (mierzoną zgodnie z ruchem wskazówek zegara) łączącego 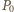 z
z 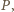 tzn. dla każdego
tzn. dla każdego 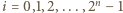
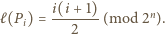
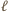 jest bijekcją zbioru wierzchołków
jest bijekcją zbioru wierzchołków 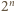 -kąta i
-kąta i ![|Z ∩ [0,2n −1].](/math/temat/matematyka/geometria/planimetria/zadania/2017/04/30/zm-1530/8x-5a02d8212f68e6296da2e894dc2a3a250bf72f4c-im-66,57,43-FF,FF,FF.gif)
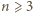 zachodzi równość
zachodzi równość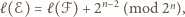
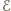 jest obrazem
jest obrazem 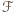 przy obrocie o
przy obrocie o 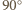 wokół środka danego okręgu zgodnie z ruchem wskazówek zegara. Konkretnie, wykażemy, że dla każdego
wokół środka danego okręgu zgodnie z ruchem wskazówek zegara. Konkretnie, wykażemy, że dla każdego 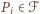
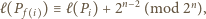
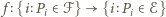 określona jest następująco
określona jest następująco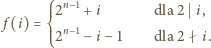
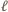 wystarczy więc sprawdzić, że dla każdego
wystarczy więc sprawdzić, że dla każdego 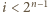 liczba
liczba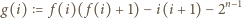
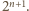 Rzeczywiście, bezpośrednio z definicji funkcji
Rzeczywiście, bezpośrednio z definicji funkcji 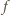 otrzymujemy, że jeżeli
otrzymujemy, że jeżeli 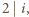 to
to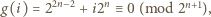
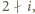 to
to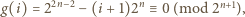
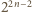 dzieli się przez
dzieli się przez 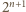 dla
dla 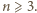 Pozostaje bezpośrednio sprawdzić, że dla
Pozostaje bezpośrednio sprawdzić, że dla 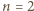 rozważane zbiory także są przystające (odpowiednia izometria znów jest obrotem o
rozważane zbiory także są przystające (odpowiednia izometria znów jest obrotem o 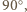 ale w przeciwną stronę).
ale w przeciwną stronę).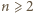 istnieje etykietowanie wierzchołków
istnieje etykietowanie wierzchołków 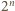 -kąta foremnego o opisanych własnościach - jest to równoważne zadaniu 2 z I etapu LX OM, którego rozwiązanie można znaleźć na stronie
-kąta foremnego o opisanych własnościach - jest to równoważne zadaniu 2 z I etapu LX OM, którego rozwiązanie można znaleźć na stronie 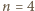 z zaznaczonymi zbiorami
z zaznaczonymi zbiorami  oraz
oraz 
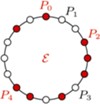
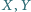 są środkami odpowiednio boków
są środkami odpowiednio boków 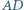 i
i 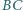 czworokąta wypukłego
czworokąta wypukłego 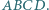 Udowodnij, że
Udowodnij, że 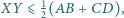 przy czym równość zachodzi wtedy i tylko wtedy, gdy
przy czym równość zachodzi wtedy i tylko wtedy, gdy 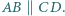
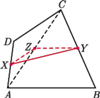
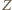 będzie środkiem przekątnej
będzie środkiem przekątnej 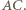 Wówczas
Wówczas 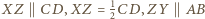 oraz
oraz 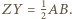 Stąd na mocy nierówności trójkąta dla punktów
Stąd na mocy nierówności trójkąta dla punktów 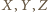 mamy
mamy 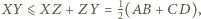 przy czym równość zachodzi wtedy i tylko wtedy, gdy
przy czym równość zachodzi wtedy i tylko wtedy, gdy 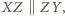 czyli gdy
czyli gdy 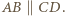
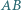 i
i 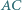 trójkąta
trójkąta 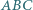 zbudowano, po jego zewnętrznej stronie, kwadraty
zbudowano, po jego zewnętrznej stronie, kwadraty 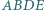 i
i 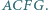 Punkty
Punkty 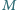 i
i 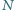 są odpowiednio środkami odcinków
są odpowiednio środkami odcinków 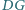 i
i 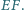 Wyznacz możliwe wartości wyrażenia
Wyznacz możliwe wartości wyrażenia 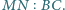
 będzie środkiem odcinka
będzie środkiem odcinka 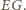 Wówczas
Wówczas 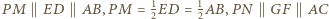 oraz
oraz 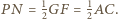 Wobec tego trójkąty
Wobec tego trójkąty 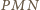 i
i 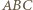 są podobne w skali
są podobne w skali 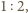 a więc
a więc 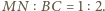
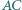 i
i 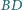 czworokąta wypukłego
czworokąta wypukłego 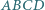 są równej długości. Punkty
są równej długości. Punkty 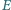 i
i 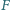 są odpowiednio środkami boków
są odpowiednio środkami boków 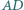 i
i 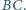 Udowodnij, że prosta
Udowodnij, że prosta 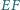 tworzy równe kąty z przekątnymi
tworzy równe kąty z przekątnymi 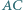 i
i 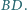

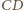 przez
przez 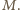 Wówczas
Wówczas 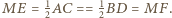 Wobec tego trójkąt
Wobec tego trójkąt 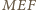 jest równoramienny i podstawa
jest równoramienny i podstawa 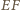 tworzy równe kąty z bokami
tworzy równe kąty z bokami 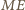 i
i 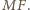 Jednocześnie
Jednocześnie 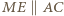 oraz
oraz 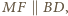 co kończy dowód.
co kończy dowód.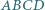 nie jest równoległobokiem oraz
nie jest równoległobokiem oraz 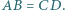 Punkty
Punkty 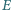 i
i 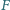 są odpowiednio środkami przekątnych
są odpowiednio środkami przekątnych 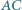 i
i 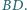 Wykaż, że rzuty prostopadłe odcinków
Wykaż, że rzuty prostopadłe odcinków 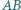 i
i 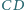 na prostą
na prostą 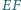 są równej długości.
są równej długości.
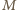 będzie środkiem boku
będzie środkiem boku 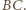 Wówczas
Wówczas 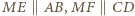 oraz
oraz 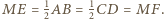 Wobec tego trójkąt
Wobec tego trójkąt 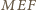 jest równoramienny (
jest równoramienny ( 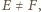 gdyż
gdyż 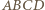 nie jest równoległobokiem). Stąd rzut
nie jest równoległobokiem). Stąd rzut 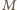 na prostą
na prostą 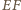 jest środkiem podstawy
jest środkiem podstawy 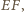 a więc rzuty boków
a więc rzuty boków 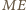 i
i 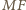 na prostą
na prostą 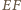 są równej długości jako połówki podstawy. Wobec tego również dwukrotnie od nich dłuższe rzuty odcinków
są równej długości jako połówki podstawy. Wobec tego również dwukrotnie od nich dłuższe rzuty odcinków 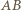 i
i 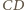 są równej długości.
są równej długości.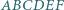 o polu 1 punkty
o polu 1 punkty 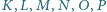 są środkami odpowiednio przekątnych
są środkami odpowiednio przekątnych 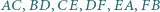 i tworzą sześciokąt wypukły
i tworzą sześciokąt wypukły 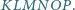 Wyznacz jego pole.
Wyznacz jego pole.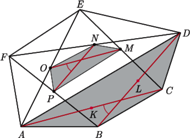
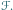
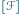
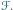
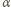 oznacza miarę nie większego z kątów pomiędzy przekątnymi
oznacza miarę nie większego z kątów pomiędzy przekątnymi 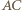 i
i 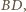 wówczas
wówczas ![|[ABCD] = 12AC⋅ BD⋅sinα .](/math/temat/matematyka/geometria/planimetria/zadania/2017/04/29/zm-17_05-deltoid-5/4x-9b80fedd92e33e6d528df9e7b09e1c2f4c115de4-im-66,57,43-FF,FF,FF.gif) Jednocześnie
Jednocześnie 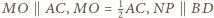 oraz
oraz 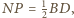 zatem kąt pomiędzy odcinkami
zatem kąt pomiędzy odcinkami 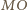 i
i 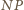 także jest równy
także jest równy 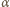 oraz
oraz![[MNOP] = 1MO⋅ NP ⋅sinα = 1CA⋅BD⋅sin α = 1[ABCD]. 2 8 4](/math/temat/matematyka/geometria/planimetria/zadania/2017/04/29/zm-17_05-deltoid-5/10x-9b80fedd92e33e6d528df9e7b09e1c2f4c115de4-dm-66,57,43-FF,FF,FF.gif)
![|[PKLM] = 14[DEFA],](/math/temat/matematyka/geometria/planimetria/zadania/2017/04/29/zm-17_05-deltoid-5/11x-9b80fedd92e33e6d528df9e7b09e1c2f4c115de4-im-66,57,43-FF,FF,FF.gif) stąd
stąd ![[KLMNOP] = 14[ABCDEF] = 14.](/math/temat/matematyka/geometria/planimetria/zadania/2017/04/29/zm-17_05-deltoid-5/12x-9b80fedd92e33e6d528df9e7b09e1c2f4c115de4-im-66,57,43-FF,FF,FF.gif)
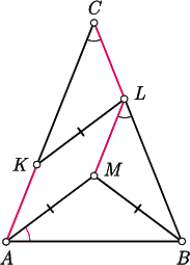
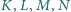 będą środkami kolejnych boków czworokąta
będą środkami kolejnych boków czworokąta 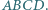 Wykaż, że
Wykaż, że 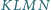 jest równoległobokiem, że
jest równoległobokiem, że 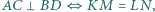 że
że 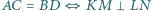 oraz wyznacz stosunek pól
oraz wyznacz stosunek pól ![N] [ABCD]. [KLM](/math/temat/matematyka/geometria/planimetria/zadania/2017/04/29/zm-17_05-deltoid-6/6x-476c50773c7ee85da9c32be7747c5f72357fd03b-im-2C,6B,73-FF,FF,FF.gif)
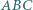 o bokach
o bokach 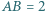 oraz
oraz 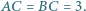 Punkt
Punkt 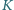 jest środkiem boku
jest środkiem boku 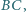 punkt
punkt 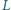 leży na boku
leży na boku 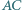 oraz
oraz 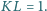 Wyznacz długość odcinka
Wyznacz długość odcinka 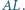
 to tylko jedna z możliwości.
to tylko jedna z możliwości.
 i nożyczki. Czy można wyciąć taką dziurę, przez którą przejdzie człowiek?
i nożyczki. Czy można wyciąć taką dziurę, przez którą przejdzie człowiek?
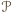 oznaczmy przez
oznaczmy przez 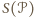 lekko zmodyfikowaną sumę miar kątów wewnętrznych wielokąta
lekko zmodyfikowaną sumę miar kątów wewnętrznych wielokąta 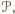 mianowicie taką, w której zamiast kątów wklęsłych występują kąty dopełniające je do pełnych ze znakiem "
mianowicie taką, w której zamiast kątów wklęsłych występują kąty dopełniające je do pełnych ze znakiem "  ". Jeżeli więc
". Jeżeli więc 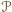 jest
jest 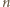 -kątem o dokładnie
-kątem o dokładnie 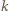 wklęsłych kątach wewnętrznych, to definiujemy
wklęsłych kątach wewnętrznych, to definiujemy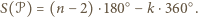
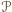 jest podzielony odcinkami na wielokąty
jest podzielony odcinkami na wielokąty 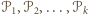 o rozłącznych wnętrzach. Wierzchołkami podziału nazwijmy te wierzchołki wielokątów
o rozłącznych wnętrzach. Wierzchołkami podziału nazwijmy te wierzchołki wielokątów 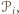 które nie są wierzchołkami wielokąta
które nie są wierzchołkami wielokąta 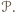 Wówczas
Wówczas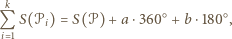
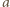 jest liczbą wierzchołków podziału wokół których znajdują się tylko kąty wypukłe wielokątów
jest liczbą wierzchołków podziału wokół których znajdują się tylko kąty wypukłe wielokątów 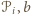 zaś jest liczbą wierzchołków podziału leżących na bokach wielokąta
zaś jest liczbą wierzchołków podziału leżących na bokach wielokąta  (w przypadku wierzchołków podziału, będących wierzchołkami pewnych kątów wklęsłych wielokątów
(w przypadku wierzchołków podziału, będących wierzchołkami pewnych kątów wklęsłych wielokątów 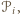 "wychodzimy na zero", zgodnie z definicją
"wychodzimy na zero", zgodnie z definicją 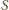 ).
).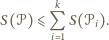
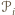 były czworokątami wklęsłymi, to
były czworokątami wklęsłymi, to 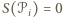 dla każdego
dla każdego 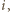 wobec czego
wobec czego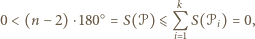
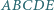 jest wpisany w okrąg
jest wpisany w okrąg 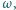 przy czym proste
przy czym proste 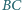 i
i 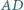 przecinają się w takim punkcie
przecinają się w takim punkcie 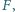 że prosta
że prosta 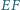 jest styczna do
jest styczna do 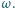 Druga prosta styczna do okręgu
Druga prosta styczna do okręgu 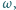 równoległa do
równoległa do 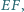 przecina proste
przecina proste 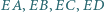 odpowiednio w punktach
odpowiednio w punktach 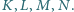 Udowodnić, że odcinki
Udowodnić, że odcinki 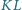 i
i 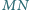 mają jednakową długość.
mają jednakową długość.
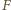 prostą różną od
prostą różną od 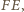 styczną do okręgu
styczną do okręgu 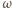 w punkcie
w punkcie 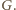 Prosta przechodząca przez punkty
Prosta przechodząca przez punkty 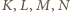 jest styczna do okręgu w punkcie
jest styczna do okręgu w punkcie 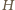 i przecina prostą
i przecina prostą 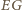 w punkcie
w punkcie 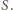 Pokażemy, że
Pokażemy, że 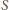 jest środkiem odcinka
jest środkiem odcinka 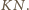 Ponieważ
Ponieważ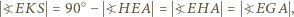
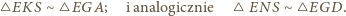
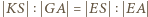 oraz
oraz 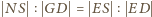 ; a z nich -
; a z nich -
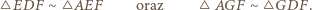
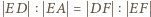 oraz
oraz 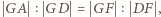 z których wynika, że prawa strona wzoru (1) jest równa
z których wynika, że prawa strona wzoru (1) jest równa 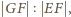 czyli 1.
czyli 1. leżą po jednej stronie punktu
leżą po jednej stronie punktu  ; punkty
; punkty  po drugiej. Uzyskana równość
po drugiej. Uzyskana równość 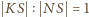 oznacza, że
oznacza, że 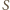 jest środkiem odcinka
jest środkiem odcinka 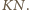 Przez analogię, ten sam punkt
Przez analogię, ten sam punkt 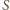 jest też środkiem odcinka
jest też środkiem odcinka 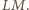 Stąd wniosek, że odcinki
Stąd wniosek, że odcinki 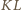 i
i 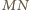 są przystające.
są przystające.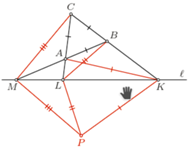
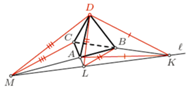
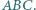 Prosta
Prosta 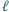 przecina proste
przecina proste 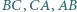 odpowiednio w punktach
odpowiednio w punktach 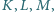 różnych od wierzchołków trójkąta. Udowodnić, że istnieje taki punkt
różnych od wierzchołków trójkąta. Udowodnić, że istnieje taki punkt 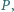 że
że 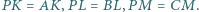
 będzie takim punktem w przestrzeni, że czworościan
będzie takim punktem w przestrzeni, że czworościan 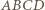 jest foremny. Wówczas trójkąt
jest foremny. Wówczas trójkąt 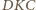 jest przystający do trójkąta
jest przystający do trójkąta 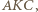 gdyż jest jego obrazem przy obrocie wokół prostej
gdyż jest jego obrazem przy obrocie wokół prostej 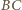 przeprowadzającym punkt
przeprowadzającym punkt 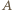 na punkt
na punkt 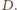 Wobec tego
Wobec tego 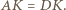
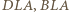 oraz
oraz 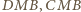 i wynikające stąd równości
i wynikające stąd równości 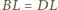 oraz
oraz 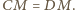 Za
Za 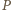 wystarczy teraz przyjąć obraz punktu
wystarczy teraz przyjąć obraz punktu 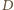 przy takim obrocie wokół prostej
przy takim obrocie wokół prostej 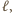 który posyła
który posyła 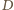 w płaszczyznę trójkąta
w płaszczyznę trójkąta 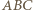 (są dwa takie punkty).
(są dwa takie punkty).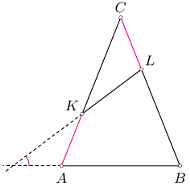
 w którym
w którym  Na odcinkach
Na odcinkach  znajdują się odpowiednio takie punkty
znajdują się odpowiednio takie punkty 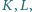 że
że 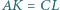 oraz
oraz 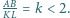 Wyznaczyć, w zależności od
Wyznaczyć, w zależności od 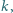 miarę kąta między prostymi
miarę kąta między prostymi  i
i 
 będzie takim punktem, że czworokąt
będzie takim punktem, że czworokąt 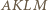 jest równoległobokiem. Wówczas
jest równoległobokiem. Wówczas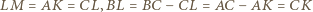
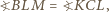
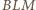 oraz
oraz 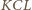 są przystające (cecha bok-kąt-bok). Zatem
są przystające (cecha bok-kąt-bok). Zatem 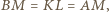 czyli trójkąt
czyli trójkąt 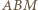 jest równoramienny, więc
jest równoramienny, więc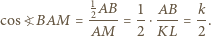
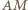 i
i 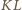 są równoległe, więc
są równoległe, więc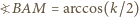
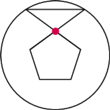
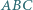 bok
bok 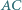 jest dłuższy niż
jest dłuższy niż 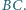 Punkt
Punkt 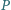 leży na dwusiecznej
leży na dwusiecznej 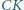 kąta
kąta 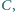 zaś punkt
zaś punkt 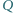 leży na środkowej
leży na środkowej 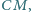 połowiącej bok
połowiącej bok 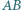 ; przy tym
; przy tym 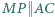 oraz
oraz 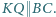 Wykazać, że odcinek
Wykazać, że odcinek 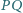 jest prostopadły do
jest prostopadły do 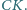
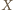 punkt przecięcia przekątnych czworokąta
punkt przecięcia przekątnych czworokąta 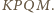 Prosta
Prosta 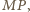 równoległa do
równoległa do 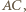 przecina bok
przecina bok 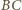 w punkcie
w punkcie 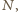 będącym środkiem tego boku. Skoro ów bok jest równoległy do
będącym środkiem tego boku. Skoro ów bok jest równoległy do 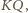 zatem punkt
zatem punkt 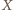 (leżący na prostej
(leżący na prostej 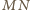 ) jest środkiem odcinka
) jest środkiem odcinka 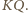
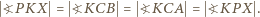
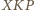 jest więc równoramienny:
jest więc równoramienny: 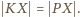 Punkt
Punkt 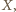 jako środek odcinka
jako środek odcinka 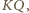 jest w takim razie środkiem okręgu opisanego na trójkącie
jest w takim razie środkiem okręgu opisanego na trójkącie 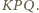 Wynika stąd, że kąt
Wynika stąd, że kąt 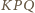 jest prosty - a to teza zadania.
jest prosty - a to teza zadania.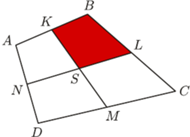
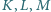 i
i 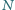 są odpowiednio środkami boków
są odpowiednio środkami boków 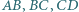 i
i 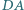 czworokąta wypukłego
czworokąta wypukłego 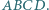 Odcinki
Odcinki 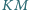 i
i 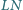 przecinają się w punkcie
przecinają się w punkcie 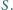 Znaleźć kres dolny i górny pola czworokąta
Znaleźć kres dolny i górny pola czworokąta 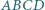 przy założeniu, że pole czworokąta
przy założeniu, że pole czworokąta 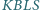 jest równe
jest równe 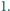
![|[ℱ]](/math/temat/matematyka/geometria/planimetria/zadania/2016/10/31/zm-1512/1x-9dbfe84ebf61bac61555ddb19dc430d0032fb9e1-im-66,57,43-FF,FF,FF.gif) oznacza pole figury
oznacza pole figury 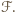
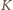 i
i 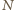 są środkami odcinków
są środkami odcinków 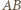 i
i 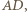 to
to 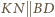 oraz
oraz 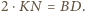 Podobnie otrzymujemy
Podobnie otrzymujemy 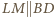 oraz
oraz 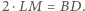 W takim razie czworokąt
W takim razie czworokąt 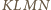 ma dwa boki równej długości i równoległe, więc jest równoległobokiem o środku
ma dwa boki równej długości i równoległe, więc jest równoległobokiem o środku 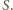 Ponadto trójkąt
Ponadto trójkąt 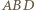 jest obrazem trójkąta
jest obrazem trójkąta 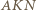 w jednokładności o środku
w jednokładności o środku 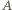 i skali
i skali 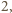 więc
więc ![]=4⋅[A].[AKBND](/math/temat/matematyka/geometria/planimetria/zadania/2016/10/31/zm-1512/15x-89a4f3d2a354815ca7ee350824d02cb970519291-im-66,57,43-FF,FF,FF.gif) Z analogicznych rozważań dla trójkątów
Z analogicznych rozważań dla trójkątów 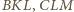 i
i 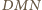 otrzymujemy
otrzymujemy![]+4⋅[BKL]+4⋅[C]+4⋅[DMN]=[ADB]+[BAC]+[CBD]+[DCA]=2⋅[ABCD].4L⋅[MAKN](/math/temat/matematyka/geometria/planimetria/zadania/2016/10/31/zm-1512/18x-89a4f3d2a354815ca7ee350824d02cb970519291-dm-66,57,43-FF,FF,FF.gif)
![N]=8⋅[KLS]. [ABCD]](/math/temat/matematyka/geometria/planimetria/zadania/2016/10/31/zm-1512/19x-89a4f3d2a354815ca7ee350824d02cb970519291-dm-66,57,43-FF,FF,FF.gif)
![4 ⋅[BKL] = [BAC]](/math/temat/matematyka/geometria/planimetria/zadania/2016/10/31/zm-1512/20x-89a4f3d2a354815ca7ee350824d02cb970519291-dm-66,57,43-FF,FF,FF.gif)
![-1 [KBLS] = [KBL] + [KLS] ⩽ 4 [ABCD]](/math/temat/matematyka/geometria/planimetria/zadania/2016/10/31/zm-1512/21x-89a4f3d2a354815ca7ee350824d02cb970519291-dm-66,57,43-FF,FF,FF.gif)
![1- [KBLS] ⩾ [KLS] = 8[ABCD].](/math/temat/matematyka/geometria/planimetria/zadania/2016/10/31/zm-1512/22x-89a4f3d2a354815ca7ee350824d02cb970519291-dm-66,57,43-FF,FF,FF.gif)
![8-⩽ [ABCD] 3](/math/temat/matematyka/geometria/planimetria/zadania/2016/10/31/zm-1512/23x-89a4f3d2a354815ca7ee350824d02cb970519291-dm-66,57,43-FF,FF,FF.gif)
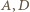 i
i 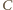 są współliniowe (wówczas
są współliniowe (wówczas ![[ABC] |](/math/temat/matematyka/geometria/planimetria/zadania/2016/10/31/zm-1512/26x-89a4f3d2a354815ca7ee350824d02cb970519291-im-66,57,43-FF,FF,FF.gif) ), a maksimum - gdy wierzchołki
), a maksimum - gdy wierzchołki 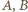 i
i 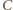 są współliniowe (wówczas
są współliniowe (wówczas ![|[ABC]](/math/temat/matematyka/geometria/planimetria/zadania/2016/10/31/zm-1512/29x-89a4f3d2a354815ca7ee350824d02cb970519291-im-66,57,43-FF,FF,FF.gif) ).
).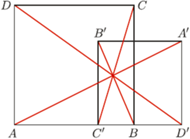
 położone są na jednej prostej w tej właśnie kolejności. Kwadraty
położone są na jednej prostej w tej właśnie kolejności. Kwadraty  i
i 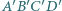 leżą po tej samej stronie tej prostej. Wykaż, że odcinki
leżą po tej samej stronie tej prostej. Wykaż, że odcinki 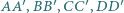 przecinają się w jednym punkcie.
przecinają się w jednym punkcie.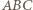 i
i 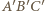 są podobne (jako połówki kwadratów) oraz są położone w sposób opisany w twierdzeniu (*). Ponadto są one niezgodnie ułożone, istnieje więc jednokładność o skali ujemnej przeprowadzająca
są podobne (jako połówki kwadratów) oraz są położone w sposób opisany w twierdzeniu (*). Ponadto są one niezgodnie ułożone, istnieje więc jednokładność o skali ujemnej przeprowadzająca 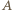 na
na 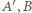 na
na 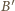 oraz
oraz 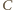 na
na 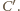 Odcinki
Odcinki 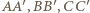 przecinają się więc w jej środku. Analogicznie odcinek
przecinają się więc w jej środku. Analogicznie odcinek 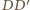 przechodzi przez punkt przecięcia odcinków
przechodzi przez punkt przecięcia odcinków 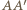 i
i 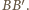
 Każda z przekątnych
Każda z przekątnych  dzieli ten sześciokąt na dwa czworokąty o równych polach. Udowodnij, że przekątne te przecinają się w jednym punkcie.
dzieli ten sześciokąt na dwa czworokąty o równych polach. Udowodnij, że przekątne te przecinają się w jednym punkcie.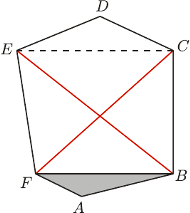
![[ℱ]](/math/temat/matematyka/geometria/planimetria/zadania/2016/10/31/zm-16_11-deltoid-2/1x-f0947e5fa2249f537e09dae26bfbbda96a771afe-im-66,57,43-FF,FF,FF.gif) oznacza pole figury
oznacza pole figury 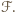 Skoro
Skoro ![1 |[BACF] = 2[BACDEF] = [ABEF],](/math/temat/matematyka/geometria/planimetria/zadania/2016/10/31/zm-16_11-deltoid-2/3x-f0947e5fa2249f537e09dae26bfbbda96a771afe-im-66,57,43-FF,FF,FF.gif) to
to ![|[FBC] = [FBE].](/math/temat/matematyka/geometria/planimetria/zadania/2016/10/31/zm-16_11-deltoid-2/4x-f0947e5fa2249f537e09dae26bfbbda96a771afe-im-66,57,43-FF,FF,FF.gif) Trójkąty te mają wspólną podstawę
Trójkąty te mają wspólną podstawę 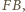 zatem mają też równe wysokości na nią. Ponieważ punkty
zatem mają też równe wysokości na nią. Ponieważ punkty 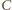 i
i 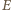 leżą po tej samej stronie prostej
leżą po tej samej stronie prostej 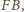 wynika stąd, że
wynika stąd, że 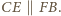 Analogicznie
Analogicznie 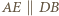 oraz
oraz 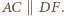
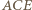 i
i 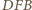 spełniają założenia twierdzenia
spełniają założenia twierdzenia 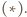 Jeden z nich jest więc obrazem drugiego w pewnej jednokładności o ujemnej skali, której środek leży na każdym z odcinków
Jeden z nich jest więc obrazem drugiego w pewnej jednokładności o ujemnej skali, której środek leży na każdym z odcinków