Zmieści się?»Zadanie 3
o zadaniu...
- Zadanie pochodzi z artykułu Zmieści się?
- Publikacja w Delcie: czerwiec 2015
- Publikacja elektroniczna: 31-05-2015
- Artykuł źródłowy w wersji do druku [application/pdf]: (55 KB)

Rys. 1
a) Kwadrat o boku 2 dzielimy na cztery kwadraty jednostkowe i w każdy z nich wpisujemy koło. Koło 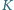 ma środek w środku kwadratu i jest styczne zewnętrznie do każdego z pozostałych kół (Rys. 1). Wyznacz jego promień
ma środek w środku kwadratu i jest styczne zewnętrznie do każdego z pozostałych kół (Rys. 1). Wyznacz jego promień 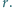
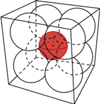
Rys. 2
b) Wyznacz promień analogicznej kuli 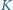 dla sześcianu o krawędzi 2 i ośmiu kul o średnicy 1 (Rys. 2).
dla sześcianu o krawędzi 2 i ośmiu kul o średnicy 1 (Rys. 2).
c) Wyznacz promień analogicznej  -wymiarowej kuli
-wymiarowej kuli 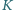 dla
dla  -wymiarowego hipersześcianu o krawędzi 2 i
-wymiarowego hipersześcianu o krawędzi 2 i 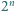 kul
kul 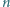 -wymiarowych o średnicy 1.
-wymiarowych o średnicy 1.
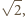 stąd
stąd 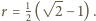
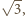 stąd
stąd 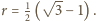
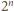 kul równa jest 1, a przekątna hipersześcianu jednostkowego ma długość
kul równa jest 1, a przekątna hipersześcianu jednostkowego ma długość 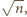 stąd
stąd 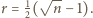
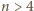 uzyskujemy
uzyskujemy 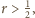 więc "mała" kulka
więc "mała" kulka 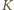 jest większa od każdej z "dużych" kul, a dla
jest większa od każdej z "dużych" kul, a dla 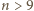 mamy
mamy 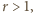 czyli kula
czyli kula 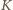 wystaje poza hipersześcian!
wystaje poza hipersześcian!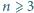 można wybrać
można wybrać 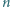 punktów na płaszczyźnie tak, aby odległość między każdymi dwoma była co najwyżej
punktów na płaszczyźnie tak, aby odległość między każdymi dwoma była co najwyżej 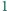 i była równa
i była równa 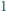 dla dokładnie
dla dokładnie 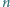 par punktów.
par punktów.
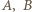 i
i 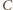 leżące w wierzchołkach trójkąta równobocznego o boku
leżące w wierzchołkach trójkąta równobocznego o boku 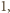 a pozostałe
a pozostałe 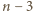 punkty z krótszego łuku
punkty z krótszego łuku 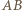 okręgu o środku
okręgu o środku 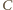 i promieniu
i promieniu 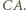
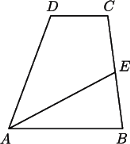
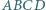 boki
boki 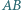 i
i 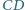 są równoległe oraz
są równoległe oraz 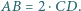 Punkt
Punkt 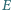 jest środkiem boku
jest środkiem boku 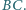 Udowodnić, że jeśli w czworokąt
Udowodnić, że jeśli w czworokąt 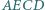 można wpisać okrąg, to
można wpisać okrąg, to 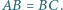
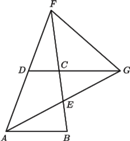
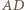 i
i 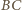 przecinają się w punkcie
przecinają się w punkcie 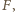 a proste
a proste 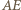 i
i 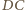 w punkcie
w punkcie 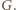
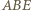 i
i 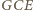 są przystające, a w szczególności
są przystające, a w szczególności 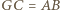 oraz
oraz 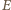 jest środkiem
jest środkiem 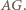 Ponadto
Ponadto 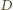 jest środkiem
jest środkiem 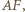 ponieważ odcinek
ponieważ odcinek 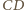 jest równoległy do
jest równoległy do 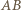 i dwa razy krótszy. Zatem
i dwa razy krótszy. Zatem 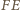 i
i 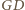 są środkowymi w trójkącie
są środkowymi w trójkącie 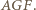
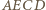 można wpisać okrąg, to zachodzi równość
można wpisać okrąg, to zachodzi równość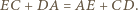
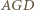 i
i 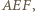 które mają równe pola (równe połowie pola trójkąta
które mają równe pola (równe połowie pola trójkąta 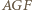 ). W takim razie mają również równe obwody, czyli
). W takim razie mają również równe obwody, czyli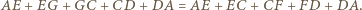
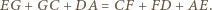
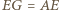 i
i 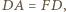 to mamy też
to mamy też 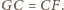 Stąd dostajemy
Stąd dostajemy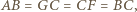

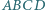 boki
boki 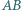 i
i 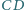 są równoległe oraz
są równoległe oraz 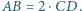 Punkt
Punkt 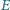 jest środkiem boku
jest środkiem boku 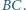 Udowodnić, że jeśli
Udowodnić, że jeśli 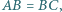 to w czworokąt
to w czworokąt 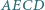 można wpisać okrąg.
można wpisać okrąg.
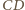 punkt
punkt 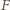 w taki sposób, aby czworokąt
w taki sposób, aby czworokąt 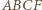 był równoległobokiem.
był równoległobokiem.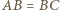 możemy wywnioskować, że
możemy wywnioskować, że 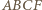 jest rombem. Ponadto, skoro
jest rombem. Ponadto, skoro 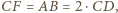 to punkt
to punkt 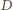 jest środkiem boku
jest środkiem boku 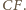 Ponieważ punkt
Ponieważ punkt 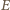 jest środkiem boku
jest środkiem boku 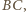 więc punkty
więc punkty 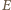 i
i 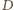 są symetryczne względem prostej
są symetryczne względem prostej 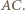 Oznacza to, że czworokąt
Oznacza to, że czworokąt 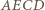 jest deltoidem, zatem w szczególności można w niego wpisać okrąg.
jest deltoidem, zatem w szczególności można w niego wpisać okrąg.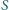 poza kartką, oraz punkt
poza kartką, oraz punkt 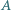 pomiędzy nimi. Korzystając wyłącznie z linijki, narysuj tę część prostej
pomiędzy nimi. Korzystając wyłącznie z linijki, narysuj tę część prostej 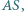 która mieści się na kartce.
która mieści się na kartce.
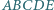 jest podstawą ostrosłupa
jest podstawą ostrosłupa 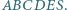 Płaszczyzna przecina krawędzie
Płaszczyzna przecina krawędzie 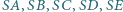 odpowiednio w punktach
odpowiednio w punktach 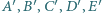 (różnych od wierzchołków ostrosłupa). Udowodnij, że punkty przecięcia przekątnych czworokątów
(różnych od wierzchołków ostrosłupa). Udowodnij, że punkty przecięcia przekątnych czworokątów 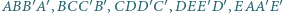 leżą na jednej płaszczyźnie.
leżą na jednej płaszczyźnie.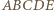 i
i 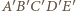 (rysunek podobny do
(rysunek podobny do 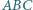 jest styczny do boków
jest styczny do boków 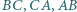 odpowiednio w punktach
odpowiednio w punktach 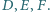 Udowodnij, że punkty
Udowodnij, że punkty 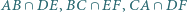 leżą na jednej prostej.
leżą na jednej prostej.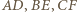 są współpękowe i wykorzystaj twierdzenie Desarguesa. Inne rozwiązanie opisano w deltoidzie 9/2014.
są współpękowe i wykorzystaj twierdzenie Desarguesa. Inne rozwiązanie opisano w deltoidzie 9/2014.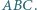 Punkty
Punkty 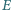 i
i 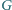 leżą na boku
leżą na boku 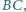 punkty
punkty 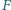 i
i 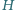 - na boku
- na boku 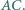 Punkty
Punkty 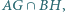
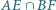 oraz punkt
oraz punkt 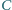 leżą na jednej prostej. Wykaż, że jeśli proste
leżą na jednej prostej. Wykaż, że jeśli proste 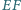 i
i 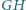 nie są równoległe, to przecinają się na prostej
nie są równoległe, to przecinają się na prostej 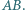
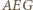 oraz
oraz 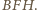

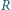 i
i  są styczne zewnętrznie. Poprowadzono ich wspólną styczną i w obszar ograniczony przez nią i okręgi wpisano okrąg. Ile wynosi jego promień?
są styczne zewnętrznie. Poprowadzono ich wspólną styczną i w obszar ograniczony przez nią i okręgi wpisano okrąg. Ile wynosi jego promień?
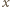 oznacza szukany promień. Jeden z trójkątów prostokątnych widocznych na rysunku ma przeciwprostokątną będącą sumą promieni o długościach
oznacza szukany promień. Jeden z trójkątów prostokątnych widocznych na rysunku ma przeciwprostokątną będącą sumą promieni o długościach 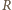 i
i  oraz przyprostokątną o długości
oraz przyprostokątną o długości 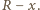 Z twierdzenia Pitagorasa otrzymujemy, że długość drugiej przyprostokątnej, a więc również długość odcinka pomiędzy odpowiednimi punktami styczności jest równa
Z twierdzenia Pitagorasa otrzymujemy, że długość drugiej przyprostokątnej, a więc również długość odcinka pomiędzy odpowiednimi punktami styczności jest równa 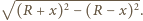
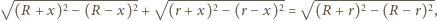
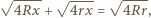
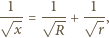
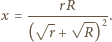
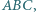 mając dany jego wierzchołek
mając dany jego wierzchołek 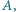 punkt
punkt 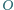 - środek okręgu opisanego i punkt
- środek okręgu opisanego i punkt 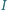 - środek okręgu wpisanego.
- środek okręgu wpisanego.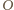 i promieniu
i promieniu 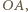
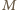 - jego punkt przecięcia z prostą
- jego punkt przecięcia z prostą 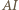 oraz okrąg o środku
oraz okrąg o środku 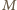 i promieniu
i promieniu 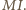 Na mocy twierdzenia
Na mocy twierdzenia 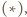 punkty przecięcia powyższych dwóch okręgów to wierzchołki
punkty przecięcia powyższych dwóch okręgów to wierzchołki 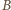 i
i 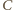 trójkąta.
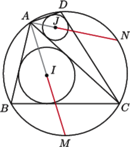
trójkąta.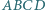 jest wpisany w okrąg
jest wpisany w okrąg 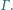 Punkt
Punkt 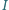 jest środkiem okręgu wpisanego w trójkąt
jest środkiem okręgu wpisanego w trójkąt 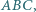 prosta
prosta 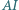 przecina okrąg
przecina okrąg 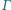 w punkcie
w punkcie 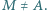 Punkt
Punkt 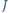 jest środkiem okręgu wpisanego w trójkąt
jest środkiem okręgu wpisanego w trójkąt 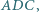 prosta
prosta 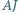 przecina okrąg
przecina okrąg 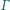 w punkcie
w punkcie 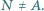 Wykaż, że jeżeli
Wykaż, że jeżeli 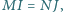 to
to 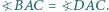
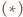 i założenia, zachodzi równość
i założenia, zachodzi równość 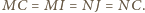 Stąd
Stąd 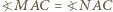 jako kąty wpisane w okrąg
jako kąty wpisane w okrąg 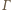 oparte na równych łukach. Wobec tego
oparte na równych łukach. Wobec tego 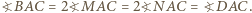
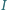 jest środkiem okręgu wpisanego w trójkąt
jest środkiem okręgu wpisanego w trójkąt 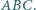 Wykaż, że okrąg opisany na trójkącie
Wykaż, że okrąg opisany na trójkącie 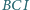 wyznacza na prostych
wyznacza na prostych 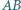 i
i 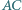 równe cięciwy.
równe cięciwy.
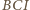 jest punkt
jest punkt 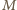 z twierdzenia
z twierdzenia 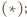 leży on na dwusiecznej kąta
leży on na dwusiecznej kąta 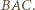 Z symetrii problemu okrąg ten wyznacza więc na ramionach kąta równe cięciwy.
Z symetrii problemu okrąg ten wyznacza więc na ramionach kąta równe cięciwy.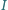 jest środkiem okręgu wpisanego w trójkąt
jest środkiem okręgu wpisanego w trójkąt 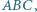 punkt
punkt 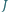 jest środkiem okręgu dopisanego do tego trójkąta. Wykaż, że środek odcinka
jest środkiem okręgu dopisanego do tego trójkąta. Wykaż, że środek odcinka 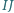 należy do okręgu opisanego na trójkącie
należy do okręgu opisanego na trójkącie 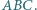
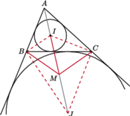
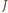 leży w kącie
leży w kącie 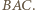 Dwusieczne kątów przyległych są prostopadłe, więc
Dwusieczne kątów przyległych są prostopadłe, więc 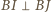 oraz
oraz 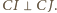 Wobec tego na czworokącie
Wobec tego na czworokącie 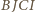 można opisać okrąg, którego środkiem jest środek
można opisać okrąg, którego środkiem jest środek 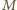 odcinka
odcinka 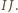 Okrąg ten jest opisany na trójkącie
Okrąg ten jest opisany na trójkącie 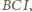 czyli
czyli 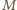 to punkt z twierdzenia
to punkt z twierdzenia 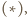 leży więc na okręgu opisanym na trójkącie
leży więc na okręgu opisanym na trójkącie 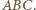
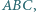 mając dane jego wierzchołki
mając dane jego wierzchołki 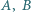 oraz promień okręgu wpisanego.
oraz promień okręgu wpisanego. jest styczny do okręgu opisanego na trójkącie
jest styczny do okręgu opisanego na trójkącie 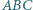 w punkcie
w punkcie 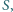 a do boków
a do boków 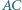 i
i 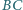 odpowiednio w punktach
odpowiednio w punktach 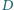 i
i 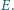 Wykaż, że jeśli
Wykaż, że jeśli 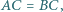 to środek okręgu wpisanego w trójkąt
to środek okręgu wpisanego w trójkąt 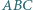 jest środkiem odcinka
jest środkiem odcinka 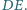
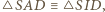 gdzie
gdzie 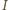 to środek odcinka
to środek odcinka 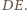
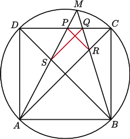
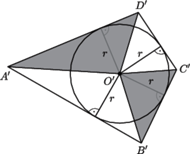
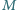 leży na krótszym łuku
leży na krótszym łuku 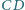 okręgu opisanego na kwadracie
okręgu opisanego na kwadracie 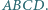 Prosta
Prosta 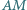 przecina
przecina 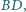
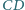 odpowiednio w punktach
odpowiednio w punktach 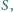
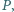 zaś prosta
zaś prosta 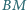 przecina
przecina 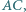
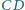 odpowiednio w punktach
odpowiednio w punktach 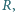
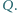 Udowodnić, że odcinki
Udowodnić, że odcinki 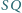 i
i 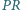 są prostopadłe.
są prostopadłe.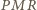 i
i 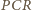 są równe (jako kąty wpisane oparte na ćwiartce okręgu), to na czworokącie
są równe (jako kąty wpisane oparte na ćwiartce okręgu), to na czworokącie 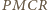 można opisać okrąg. Zatem
można opisać okrąg. Zatem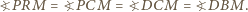
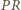 i
i 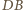 są równoległe. Rozważając czworokąt
są równoległe. Rozważając czworokąt 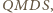 wykażemy analogicznie, że
wykażemy analogicznie, że 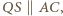 a stąd łatwo wywnioskować tezę.
a stąd łatwo wywnioskować tezę.
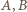 będą dwoma punktami z tej siódemki, których odległość jest maksymalna. Pozostałe punkty leżą w "soczewce", ograniczonej łukami okręgów o środkach
będą dwoma punktami z tej siódemki, których odległość jest maksymalna. Pozostałe punkty leżą w "soczewce", ograniczonej łukami okręgów o środkach 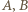 i promieniu
i promieniu 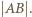 Skoro każdy z tych pięciu punktów ma wraz z
Skoro każdy z tych pięciu punktów ma wraz z 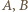 tworzyć trójkąt równoramienny, mogą one leżeć jedynie na owych łukach oraz odcinku
tworzyć trójkąt równoramienny, mogą one leżeć jedynie na owych łukach oraz odcinku 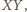 łączącym ich wspólne końce. Na samym odcinku
łączącym ich wspólne końce. Na samym odcinku 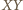 leżą co najwyżej dwa punkty (trójka współliniowa nie tworzy trójkąta). Pozostałe trzy punkty leżą na łukach
leżą co najwyżej dwa punkty (trójka współliniowa nie tworzy trójkąta). Pozostałe trzy punkty leżą na łukach 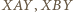 (bez końców
(bez końców 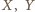 ).
).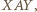 bowiem wraz z punktem
bowiem wraz z punktem 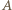 dałoby to czwórkę punktów, spośród których pewne trzy nie tworzyłyby trójkąta równoramiennego. Zatem na jednym łuku, np.
dałoby to czwórkę punktów, spośród których pewne trzy nie tworzyłyby trójkąta równoramiennego. Zatem na jednym łuku, np. 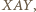 leży jeden punkt
leży jeden punkt 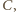 zaś na łuku
zaś na łuku 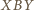 dwa punkty
dwa punkty 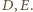 Przyjmijmy, że
Przyjmijmy, że 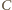 leży między
leży między 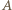 i
i 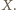
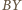 jest oddalony od
jest oddalony od 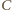 o odcinek dłuższy niż
o odcinek dłuższy niż 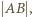 więc
więc 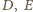 muszą być punktami łuku
muszą być punktami łuku 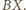 Każdy z odcinków
Każdy z odcinków 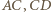 ma wtedy długość mniejszą niż
ma wtedy długość mniejszą niż 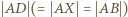 ; warunek równoramienności trójkąta
; warunek równoramienności trójkąta 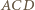 wymusza równość
wymusza równość 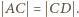 Zastępując w tym rozumowaniu
Zastępując w tym rozumowaniu 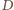 przez
przez 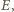 dostajemy równość
dostajemy równość 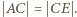 Wobec tego
Wobec tego 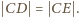 To już jest oczekiwana sprzeczność, bo jedynym punktem łuku
To już jest oczekiwana sprzeczność, bo jedynym punktem łuku 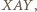 położonym w równych odległościach od
położonym w równych odległościach od 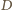 i
i 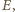 czyli na symetralnej odcinka
czyli na symetralnej odcinka 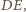 jest punkt
jest punkt 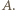
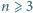 różnych punktów, które nie leżą wszystkie na jednej prostej. Udowodnić, że istnieje co najmniej
różnych punktów, które nie leżą wszystkie na jednej prostej. Udowodnić, że istnieje co najmniej 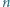 różnych prostych, z których każda zawiera co najmniej dwa spośród danych punktów.
różnych prostych, z których każda zawiera co najmniej dwa spośród danych punktów.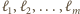 będą wszystkimi prostymi, które zawierają co najmniej dwa spośród danych punktów. Dla dowodu nie wprost załóżmy, że
będą wszystkimi prostymi, które zawierają co najmniej dwa spośród danych punktów. Dla dowodu nie wprost załóżmy, że 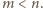 Zauważmy, że wówczas możliwe jest przyporządkowanie każdemu punktowi jednej z liczb rzeczywistych
Zauważmy, że wówczas możliwe jest przyporządkowanie każdemu punktowi jednej z liczb rzeczywistych 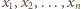 w taki sposób, aby suma na każdej prostej
w taki sposób, aby suma na każdej prostej 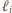 była równa
była równa 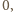 ale aby nie wszystkie liczby
ale aby nie wszystkie liczby 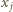 były równe
były równe 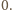 Wynika to natychmiast z faktu, iż jednorodny układ równań liniowych
Wynika to natychmiast z faktu, iż jednorodny układ równań liniowych
 równaniach i
równaniach i 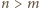 niewiadomych ma nietrywialne rozwiązanie.
niewiadomych ma nietrywialne rozwiązanie.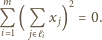
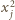 oraz
oraz 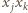 dla
dla 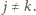 Skoro nie wszystkie punkty leżą na jednej prostej, to każdy punkt pojawia się na co najmniej dwóch prostych, a zatem każdy składnik postaci
Skoro nie wszystkie punkty leżą na jednej prostej, to każdy punkt pojawia się na co najmniej dwóch prostych, a zatem każdy składnik postaci 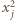 występuje co najmniej dwukrotnie w powyższej sumie. Co więcej, ponieważ przez dwa różne punkty przechodzi dokładnie jedna prosta, liczby
występuje co najmniej dwukrotnie w powyższej sumie. Co więcej, ponieważ przez dwa różne punkty przechodzi dokładnie jedna prosta, liczby 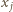 i
i 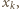 gdzie
gdzie 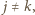 znajdą się razem w dokładnie jednej sumie. A zatem przy składniku
znajdą się razem w dokładnie jednej sumie. A zatem przy składniku 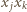 znajduje się współczynnik
znajduje się współczynnik 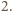 W tej sytuacji
W tej sytuacji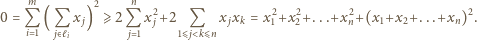
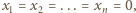 co stanowi sprzeczność z wyborem liczb
co stanowi sprzeczność z wyborem liczb 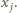 Kończy to dowód.
Kończy to dowód.
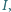 wpisany w trójkąt
wpisany w trójkąt 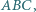 jest styczny do boku
jest styczny do boku 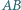 w punkcie
w punkcie 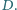 Punkt
Punkt 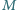 jest środkiem boku
jest środkiem boku 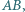 punkt
punkt 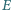 jest symetryczny do punktu
jest symetryczny do punktu 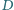 względem
względem 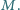 Udowodnić, że proste
Udowodnić, że proste 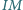 oraz
oraz 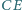 są równoległe.
są równoległe.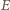 jest punktem styczności z bokiem
jest punktem styczności z bokiem 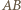 okręgu dopisanego do trójkąta
okręgu dopisanego do trójkąta 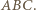 Jeżeli więc przez
Jeżeli więc przez 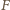 oznaczymy punkt środkowosymetryczny do
oznaczymy punkt środkowosymetryczny do 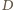 względem
względem 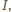 to jednokładność o środku w punkcie
to jednokładność o środku w punkcie 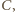 która przekształca okrąg wpisany na okrąg dopisany, przeprowadza punkt
która przekształca okrąg wpisany na okrąg dopisany, przeprowadza punkt 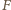 na punkt
na punkt 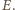 A zatem punkty
A zatem punkty 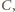
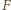 i
i 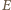 są współliniowe. Prosta
są współliniowe. Prosta 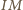 jest zatem prostą łączącą środki boków w trójkącie
jest zatem prostą łączącą środki boków w trójkącie 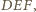 a stąd wynika żądana równoległość.
a stąd wynika żądana równoległość.
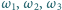 mają wspólny punkt
mają wspólny punkt 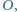 a ponadto
a ponadto 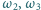 przecinają się jeszcze w punkcie
przecinają się jeszcze w punkcie 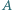 i podobnie
i podobnie 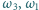 i
i 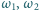 - w punkcie
- w punkcie 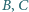 odpowiednio. Prosta
odpowiednio. Prosta 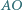 przecina
przecina 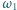 ponadto w punkcie
ponadto w punkcie 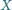 i podobnie
i podobnie 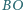 przecina
przecina 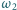 w
w 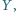 a
a 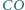 przecina
przecina 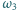 w
w 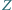 (rysunek). Udowodnić, że
(rysunek). Udowodnić, że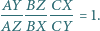
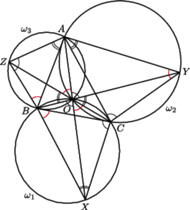
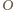 jak następuje:
jak następuje: 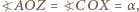
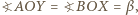
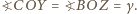
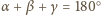 oraz na mocy tw. o kątach wpisanych,
oraz na mocy tw. o kątach wpisanych, 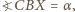
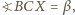 więc kąty w trójkącie
więc kąty w trójkącie 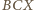 wynoszą
wynoszą 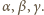 Analogicznie jest dla trójkątów
Analogicznie jest dla trójkątów 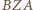 i
i 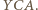 Zatem są to trójkąty podobne do trójkąta
Zatem są to trójkąty podobne do trójkąta 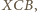 w szczególności
w szczególności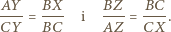
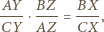

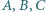 są trzema kolejnymi wierzchołkami pięciokąta foremnego wpisanego w okrąg o promieniu
są trzema kolejnymi wierzchołkami pięciokąta foremnego wpisanego w okrąg o promieniu 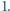 Obliczyć
Obliczyć 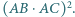

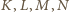 to środki odcinków).
to środki odcinków).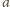 oznacza długość boku pięciokąta oraz
oznacza długość boku pięciokąta oraz 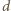 - długość przekątnej. Z podobieństwa trójkątów
- długość przekątnej. Z podobieństwa trójkątów 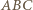 i
i 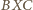 mamy
mamy 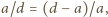 skąd
skąd 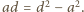 Z podobieństwa trójkątów
Z podobieństwa trójkątów 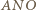 i
i 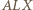 otrzymujemy
otrzymujemy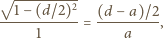
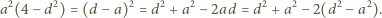
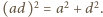 Wreszcie z podobieństwa trójkątów
Wreszcie z podobieństwa trójkątów 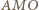 i
i 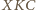 i
i 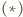 mamy
mamy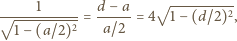
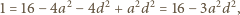
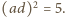
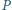 zaznaczono
zaznaczono 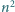 różnych punktów. Dla każdej liczby całkowitej
różnych punktów. Dla każdej liczby całkowitej 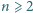 znaleźć największą możliwą liczbę prostokątów, w których każdy wierzchołek jest jednym z zaznaczonych punktów, a boki są równoległe do boków prostokąta
znaleźć największą możliwą liczbę prostokątów, w których każdy wierzchołek jest jednym z zaznaczonych punktów, a boki są równoległe do boków prostokąta 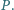
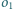 i
i 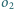 o środkach odpowiednio
o środkach odpowiednio 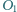 i
i 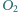 przecinają się w dwóch różnych punktach
przecinają się w dwóch różnych punktach 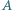 i
i 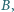 przy czym kąt
przy czym kąt 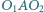 jest rozwarty. Prosta
jest rozwarty. Prosta 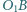 przecina okrąg
przecina okrąg 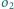 w punkcie
w punkcie 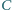 różnym od
różnym od 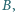 a prosta
a prosta 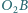 przecina okrąg
przecina okrąg 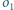 w punkcie
w punkcie 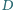 różnym od
różnym od 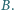 Wykazać, że punkt
Wykazać, że punkt 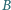 jest środkiem okręgu wpisanego w trójkąt
jest środkiem okręgu wpisanego w trójkąt 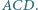
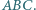 Rozważamy trzy elipsy: każda z nich ma ogniska w dwóch wierzchołkach tego trójkąta i przechodzi przez trzeci wierzchołek. Pokazać, że te trzy elipsy mają punkt wspólny wtedy i tylko wtedy, gdy trójkąt
Rozważamy trzy elipsy: każda z nich ma ogniska w dwóch wierzchołkach tego trójkąta i przechodzi przez trzeci wierzchołek. Pokazać, że te trzy elipsy mają punkt wspólny wtedy i tylko wtedy, gdy trójkąt 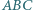 jest prostokątny.
jest prostokątny.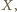 leżący w odległościach
leżący w odległościach 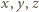 odpowiednio od wierzchołków
odpowiednio od wierzchołków 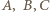 zadanego trójkąta, o bokach długości
zadanego trójkąta, o bokach długości 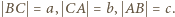 Elipsa o ogniskach
Elipsa o ogniskach 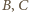 przechodzi przez punkty
przechodzi przez punkty 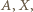 więc
więc 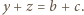 Analogicznie
Analogicznie 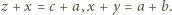 Ten układ równań z niewiadomymi
Ten układ równań z niewiadomymi 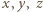 ma jedyne rozwiązanie
ma jedyne rozwiązanie 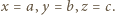 Odległości punktu
Odległości punktu 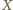 od
od 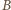 oraz
oraz 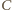 wynoszą więc, odpowiednio,
wynoszą więc, odpowiednio, 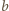 oraz
oraz  - czyli przeciwnie niż odległości punktu
- czyli przeciwnie niż odległości punktu 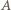 od
od 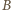 oraz
oraz 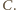 To wyznacza dwa możliwe położenia punktu
To wyznacza dwa możliwe położenia punktu 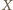 - może to być punkt symetryczny do
- może to być punkt symetryczny do 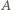 względem symetralnej odcinka
względem symetralnej odcinka 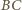 lub punkt symetryczny do
lub punkt symetryczny do 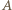 względem środka odcinka
względem środka odcinka 
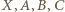 są wierzchołkami trapezu równoramiennego
są wierzchołkami trapezu równoramiennego 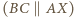 ; w drugim - tworzą równoległobok
; w drugim - tworzą równoległobok 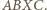 Dodatkowa informacja, że
Dodatkowa informacja, że 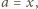 czyli
czyli 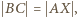 daje w obu przypadkach wniosek, że ów czworokąt jest prostokątem. A zatem trójkąt
daje w obu przypadkach wniosek, że ów czworokąt jest prostokątem. A zatem trójkąt 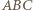 jest prostokątny.
jest prostokątny. licząc od wierzchołka.
licząc od wierzchołka. jest środkiem elipsy wpisanej w czworokąt
jest środkiem elipsy wpisanej w czworokąt 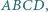 to
to
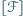 oznacza pole figury
oznacza pole figury 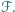
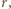 obrazem punktu
obrazem punktu 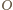 jest środek okręgu
jest środek okręgu 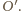 Czworokąt
Czworokąt 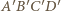 jest opisany na okręgu, zachodzi więc równość
jest opisany na okręgu, zachodzi więc równość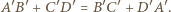
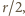 uzyskujemy tezę dla okręgu. Przekształcenia afiniczne zachowują równość pól, zatem teza zachodzi także dla wyjściowej elipsy.
uzyskujemy tezę dla okręgu. Przekształcenia afiniczne zachowują równość pól, zatem teza zachodzi także dla wyjściowej elipsy.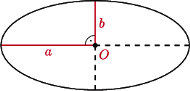
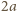 i
i 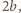 równoległych do jej półosi. Powinowactwo prostokątne o skali
równoległych do jej półosi. Powinowactwo prostokątne o skali 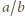 i o osi zawierającej dużą półoś elipsy przekształca nasz prostokąt na kwadrat, a elipsę na koło weń wpisane. Stąd stosunek pola
i o osi zawierającej dużą półoś elipsy przekształca nasz prostokąt na kwadrat, a elipsę na koło weń wpisane. Stąd stosunek pola 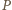 elipsy do pola
elipsy do pola 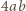 prostokąta równy jest stosunkowi pola koła do pola kwadratu na nim opisanego, czyli
prostokąta równy jest stosunkowi pola koła do pola kwadratu na nim opisanego, czyli 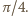 Wobec tego
Wobec tego 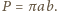
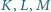 leżą odpowiednio na bokach
leżą odpowiednio na bokach 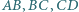 równoległoboku
równoległoboku 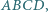 przy czym
przy czym
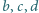 przechodzą odpowiednio przez punkty
przechodzą odpowiednio przez punkty 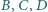 oraz są równoległe odpowiednio do prostych
oraz są równoległe odpowiednio do prostych 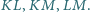 Udowodnij, że proste
Udowodnij, że proste 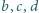 przecinają się w jednym punkcie.
przecinają się w jednym punkcie.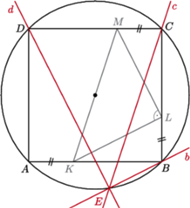
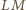 powstaje z odcinka
powstaje z odcinka 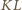 przez obrót o
przez obrót o 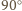 wokół środka kwadratu, zatem
wokół środka kwadratu, zatem 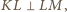 więc także
więc także 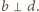 Stąd punkt
Stąd punkt 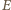 przecięcia prostych
przecięcia prostych 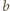 i
i 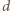 leży na okręgu opisanym na kwadracie. Ponadto skoro
leży na okręgu opisanym na kwadracie. Ponadto skoro 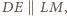 to punkt
to punkt 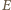 musi należeć do tego łuku
musi należeć do tego łuku 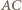 okręgu, który zawiera
okręgu, który zawiera 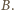 Wobec tego
Wobec tego 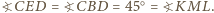 Na mocy
Na mocy 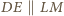 wynika stąd, iż
wynika stąd, iż 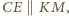 czyli
czyli 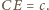 Zatem proste
Zatem proste 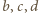 przecinają się w jednym punkcie
przecinają się w jednym punkcie