Twierdzenie o trójzębie»Zadanie 6
o zadaniu...
- Zadanie pochodzi z artykułu Twierdzenie o trójzębie
- Publikacja w Delcie: marzec 2019
- Publikacja elektroniczna: 1 marca 2019
- Artykuł źródłowy w wersji do druku [application/pdf]: (371 KB)
Okrąg wpisany w trójkąt 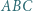 jest styczny do odcinków
jest styczny do odcinków 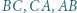 w punktach odpowiednio
w punktach odpowiednio 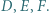 Niech
Niech 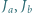 i
i 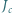 będą odpowiednio środkami okręgów wpisanych w trójkąty
będą odpowiednio środkami okręgów wpisanych w trójkąty 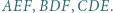 Prosta
Prosta 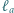 jest symetryczna do prostej
jest symetryczna do prostej 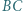 względem prostej
względem prostej 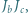 analogicznie określamy proste
analogicznie określamy proste 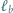 i
i 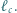 Dowieść, że proste
Dowieść, że proste 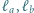 i
i 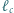 przecinają się w jednym punkcie.
przecinają się w jednym punkcie.

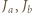 i
i 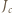 są środkami łuków
są środkami łuków 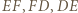 okręgu opisanego na trójkącie
okręgu opisanego na trójkącie 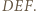 Punkt
Punkt 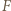 i środek
i środek 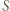 okręgu wpisanego w trójkąt
okręgu wpisanego w trójkąt 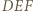 są symetryczne względem prostej
są symetryczne względem prostej 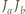 (por. poprzednie zadanie), więc
(por. poprzednie zadanie), więc 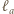 przechodzi przez punkt
przechodzi przez punkt