Zadanie ZM-1411
o zadaniu...
- Publikacja w Delcie: luty 2014
- Publikacja elektroniczna: 31-01-2014
W trójkącie
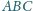 okrąg wpisany jest styczny do boków
okrąg wpisany jest styczny do boków
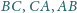 odpowiednio w punktach
odpowiednio w punktach
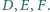 Punkty
Punkty
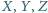 zostały obrane odpowiednio na bokach
zostały obrane odpowiednio na bokach
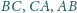 tak,
że
tak,
że
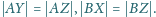 Dowieść, że prosta
Dowieść, że prosta
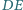 połowi
odcinek
połowi
odcinek

Wysokości pewnego trójkąta mają długości odpowiednio
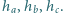 Wykaż,
że z odcinków o długościach
Wykaż,
że z odcinków o długościach
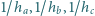 można zbudować
trójkąt.
można zbudować
trójkąt.
Przeciwległe krawędzie czworościanu mają długości odpowiednio
 i
i
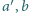 i
i
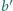 oraz
oraz
 i
i
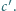 Wykaż, że
z odcinków o długościach
Wykaż, że
z odcinków o długościach
 można zbudować
trójkąt.
można zbudować
trójkąt.
Punkt
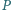 leży wewnątrz trójkąta równobocznego
leży wewnątrz trójkąta równobocznego
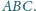 Wykaż,
że z odcinków o długościach
Wykaż,
że z odcinków o długościach
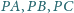 można zbudować
trójkąt.
można zbudować
trójkąt.
Dany jest równoległobok
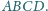 Punkty
Punkty
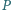 i
i
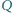 leżą
odpowiednio na bokach
leżą
odpowiednio na bokach
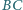 i
i
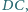 odcinki
odcinki
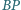 i
i
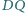 mają
jednakową długość. Dowieść, że odcinki
mają
jednakową długość. Dowieść, że odcinki
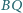 i
i
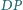 przecinają
się w punkcie, leżącym na dwusiecznej kąta
przecinają
się w punkcie, leżącym na dwusiecznej kąta
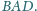
Okręgi
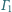 i
i
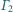 są rozłączne zewnętrznie, a ich wspólne
styczne zewnętrzne przecinają się w punkcie
są rozłączne zewnętrznie, a ich wspólne
styczne zewnętrzne przecinają się w punkcie
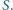 Okrąg
Okrąg
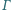 jest
styczny zewnętrznie do okręgów
jest
styczny zewnętrznie do okręgów
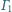 i
i
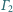 odpowiednio
w punktach
odpowiednio
w punktach
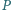 i
i
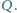 Wykaż, że punkty
Wykaż, że punkty
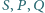 są
współliniowe.
są
współliniowe.
Dany jest trójkąt równoramienny
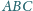 o podstawie
o podstawie
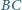 i okrąg
i okrąg
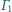 opisany na tym trójkącie. Okrąg
opisany na tym trójkącie. Okrąg
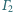 jest styczny do prostej
jest styczny do prostej
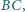 ale nie do odcinka
ale nie do odcinka
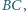 oraz do tego łuku
oraz do tego łuku
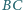 okręgu
okręgu
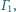 do którego należy punkt
do którego należy punkt
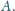 Prosta
Prosta
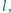 przechodząca przez
punkt
przechodząca przez
punkt
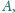 jest styczna do okręgu
jest styczna do okręgu
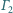 w punkcie
w punkcie
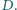 Wykaż,
że
Wykaż,
że
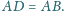
Okręgi
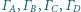 są styczne wewnętrznie do okręgu
są styczne wewnętrznie do okręgu
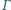 odpowiednio
w punktach
odpowiednio
w punktach
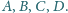 Ponadto okręgi
Ponadto okręgi
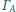 i
i
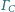 są styczne
zewnętrznie do obu okręgów
są styczne
zewnętrznie do obu okręgów
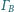 i
i
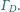 Proste styczne do
okręgu
Proste styczne do
okręgu
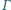 w punktach
w punktach
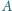 i
i
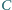 przecinają się w punkcie
przecinają się w punkcie
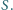 Udowodnij, że punkty
Udowodnij, że punkty
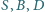 leżą na jednej prostej.
leżą na jednej prostej.
Zadanie 4 pochodzi z obozu naukowego Olimpiady Matematycznej z roku 2004.
Okręgi
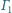 i
i
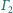 są styczne zewnętrznie i styczne do prostej
są styczne zewnętrznie i styczne do prostej
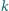 odpowiednio w punktach
odpowiednio w punktach
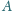 i
i
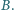 Odcinek
Odcinek
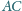 jest
średnicą okręgu
jest
średnicą okręgu
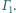 Prosta
Prosta
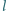 przechodzi przez punkt
przechodzi przez punkt
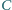 i jest styczna do okręgu
i jest styczna do okręgu
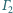 w punkcie
w punkcie
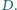 Wykaż, że
Wykaż, że
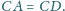
Na płaszczyźnie dane są rozłączne wewnętrznie okręgi
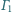 i
i
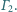 Do
każdego z nich styczny jest każdy z
Do
każdego z nich styczny jest każdy z
 okręgów
okręgów
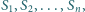 ponadto
dla każdego
ponadto
dla każdego
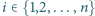 okrąg
okrąg
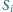 styczny jest do okręgu
styczny jest do okręgu
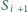 (przy czym
(przy czym
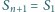 ). Dla jakich
). Dla jakich
 istnieje taki łańcuch
okręgów
istnieje taki łańcuch
okręgów
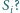 W jaki sposób zależy to od rozmiarów i wzajemnego
położenia okręgów
W jaki sposób zależy to od rozmiarów i wzajemnego
położenia okręgów
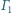 i
i
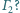 Czy i jak zależy to od wyboru
początkowego okręgu
Czy i jak zależy to od wyboru
początkowego okręgu
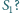
Zadanie zawodów II stopnia
Czy istnieje taki trójkat ostrokątny, w którym długości wszystkich boków i wszystkich wysokości są liczbami całkowitymi? Odpowiedź uzasadnij.
Dany jest trójkąt równoboczny
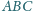 oraz punkt
oraz punkt
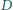 na
boku
na
boku
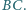 Punkty
Punkty
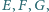 leżące odpowiednio na bokach
leżące odpowiednio na bokach
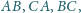 są wyznaczone przez warunki
są wyznaczone przez warunki
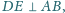
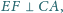
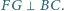 Proste
Proste
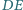 i
i
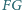 przecinają się
w punkcie
przecinają się
w punkcie
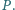 W jakim stosunku prosta
W jakim stosunku prosta
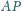 dzieli odcinek
dzieli odcinek
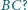
Wyznacz obraz kwadratu opisanego na okręgu w inwersji względem tego okręgu.
Okrąg o środku w punkcie
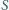 i wpisany w czworokąt wypukły
i wpisany w czworokąt wypukły
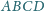 jest styczny do boków
jest styczny do boków
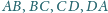 odpowiednio
w punktach
odpowiednio
w punktach
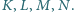 Proste
Proste
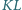 i
i
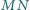 przecinają
się w punkcie
przecinają
się w punkcie
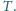 Wykaż, że proste
Wykaż, że proste
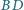 i
i
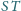 są
prostopadłe.
są
prostopadłe.
Każdy z rozłącznych okręgów
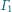 i
i
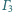 jest styczny zewnętrznie
do każdego z rozłącznych okręgów
jest styczny zewnętrznie
do każdego z rozłącznych okręgów
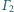 i
i
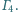 Wykaż, że punkty
styczności leżą na jednym okręgu.
Wykaż, że punkty
styczności leżą na jednym okręgu.
W czworokącie wypukłym
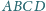 okręgi wpisane w trójkąty
okręgi wpisane w trójkąty
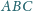 i
i
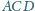 są styczne. Wykaż, że ich punkty styczności
z bokami czworokąta leżą na jednym okręgu.
są styczne. Wykaż, że ich punkty styczności
z bokami czworokąta leżą na jednym okręgu.
Dany jest trójkąt równoboczny
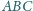 oraz dowolny punkt
oraz dowolny punkt
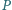 na
jego okręgu wpisanym. Wykaż, że suma
na
jego okręgu wpisanym. Wykaż, że suma
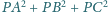 nie zależy od
wyboru punktu
nie zależy od
wyboru punktu
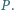
W czworokącie wypukłym
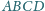 punkty
punkty
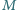 i
i
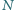 są
odpowiednio środkami boków
są
odpowiednio środkami boków
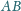 i
i
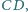 zaś przekątne
przecinają się w punkcie
zaś przekątne
przecinają się w punkcie
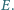 Wykaż, że prosta zawierająca dwusieczną
kąta
Wykaż, że prosta zawierająca dwusieczną
kąta
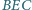 jest prostopadła do prostej
jest prostopadła do prostej
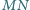 wtedy i tylko wtedy, gdy
wtedy i tylko wtedy, gdy