Zadanie ZM-1435
o zadaniu...
- Publikacja w Delcie: październik 2014
- Publikacja elektroniczna: 31-10-2014
Okrąg wpisany w trójkąt 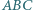 jest styczny do boków
jest styczny do boków 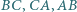 odpowiednio w punktach
odpowiednio w punktach 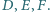 Udowodnij, że punkty
Udowodnij, że punkty 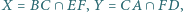
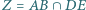 leżą na jednej prostej.
leżą na jednej prostej.
Na czworokącie 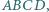 który nie jest trapezem, opisano okrąg. Wykaż, że punkty
który nie jest trapezem, opisano okrąg. Wykaż, że punkty 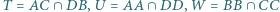 leżą na jednej prostej.
leżą na jednej prostej.
Punkty 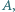
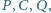
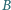 leżą w tej kolejności na łuku okręgu
leżą w tej kolejności na łuku okręgu 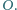 Na odcinkach
Na odcinkach 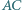 i
i 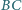 wybrano takie punkty odpowiednio
wybrano takie punkty odpowiednio 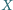 i
i 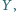 że
że 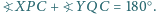 Wykaż, że wszystkie otrzymane w ten sposób proste
Wykaż, że wszystkie otrzymane w ten sposób proste 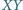 (przy ustalonych punktach
(przy ustalonych punktach 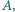
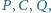
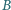 ) mają punkt wspólny.
) mają punkt wspólny.
Dany jest trójkąt 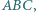 w którym
w którym 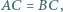 i takie punkty
i takie punkty 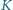 i
i 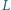 w jego wnętrzu, że
w jego wnętrzu, że 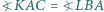 oraz
oraz 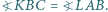 Udowodnij, że punkty
Udowodnij, że punkty 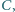
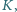
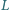 są współliniowe.
są współliniowe.
Okrąg 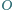 jest styczny do okręgu
jest styczny do okręgu 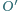 opisanego na trójkącie
opisanego na trójkącie 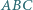 w punkcie
w punkcie 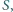 a do boków
a do boków 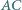 i
i 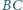 odpowiednio w punktach
odpowiednio w punktach 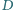 i
i 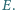 Wykaż, że środek okręgu wpisanego w trójkąt
Wykaż, że środek okręgu wpisanego w trójkąt 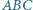 jest środkiem odcinka
jest środkiem odcinka 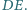
Punkt 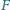 leży na boku
leży na boku 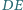 pięciokąta wypukłego
pięciokąta wypukłego 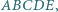 przy czym
przy czym 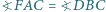 oraz
oraz 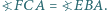 Wykaż, że
Wykaż, że 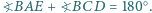
Dane są liczby dodatnie
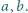 Rozważmy trójkąty prostokątne
Rozważmy trójkąty prostokątne
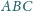 o kącie prostym przy wierzchołku
o kącie prostym przy wierzchołku
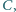 dla których
dla których
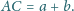 Niech
Niech
 będzie punktem na
będzie punktem na
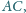 dla którego
dla którego
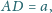
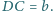 Znaleźć długość boku
Znaleźć długość boku
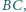 dla
której kąt
dla
której kąt
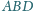 jest maksymalny.
jest maksymalny.
Dany jest kwadrat
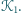 Na jednym z jego boków, na zewnątrz,
zbudowano trzy sąsiadujące kolejno kwadraty
Na jednym z jego boków, na zewnątrz,
zbudowano trzy sąsiadujące kolejno kwadraty
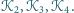 Udowodnić,
że odcinki łączące odpowiednio środki kwadratów
Udowodnić,
że odcinki łączące odpowiednio środki kwadratów
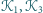 oraz
oraz
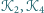 są prostopadłe.
są prostopadłe.
Proste
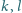 są styczne do okręgu
są styczne do okręgu
 w punktach
w punktach
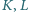 i przecinają
się w punkcie
i przecinają
się w punkcie
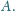 Punkt
Punkt
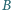 jest środkiem odcinka
jest środkiem odcinka
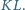 Wykazać, że punkty
Wykazać, że punkty
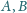 są symetryczne względem okręgu
są symetryczne względem okręgu
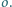
Okręgi
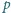 i
i
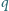 przecinają się w punktach
przecinają się w punktach
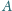 i
i
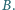 Prosta
Prosta
 jest styczna do tych okręgów w punktach odpowiednio
jest styczna do tych okręgów w punktach odpowiednio
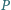 i
i
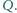 Punkt
Punkt
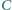 jest środkiem odcinka
jest środkiem odcinka
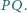 Wykazać,
że punkty
Wykazać,
że punkty
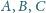 są współliniowe.
są współliniowe.
Okręgi
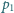 i
i
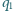 przecinają się w punktach
przecinają się w punktach
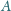 i
i
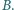 Prosta
Prosta
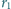 jest styczna do tych okręgów w punktach odpowiednio
jest styczna do tych okręgów w punktach odpowiednio
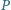 i
i
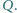 Punkt
Punkt
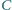 jest symetryczny do punktu
jest symetryczny do punktu
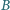 względem prostej
względem prostej
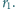 Okrąg
Okrąg
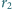 jest opisany na trójkącie
jest opisany na trójkącie
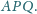 Proste
Proste
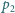 i
i
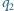 styczne do
styczne do
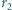 w punktach
odpowiednio
w punktach
odpowiednio
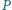 i
i
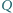 przecinają się w punkcie
przecinają się w punkcie
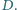 Wykazać,
że punkty
Wykazać,
że punkty
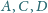 są współliniowe.
są współliniowe.
Dane są dwa przystające okręgi, przecinające się w punktach 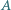 i
i 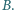 Punkt
Punkt 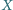 leży na jednym z tych okręgów, punkt
leży na jednym z tych okręgów, punkt 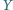 na drugim, przy czym prosta
na drugim, przy czym prosta 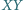 nie przechodzi ani przez
nie przechodzi ani przez 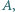 ani przez
ani przez 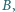 ani przez środek odcinka
ani przez środek odcinka 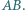 Punkt
Punkt 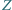 jest wierzchołkiem równoległoboku
jest wierzchołkiem równoległoboku 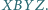 Dowieść, że okręgi opisane na trójkątach
Dowieść, że okręgi opisane na trójkątach 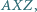
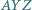 są przystające do dwóch danych okręgów.
są przystające do dwóch danych okręgów.
Rysunek z książki When Less is More, C. Alsina i R. Nelsen, MAA 2009.
Wykaż, że pole dowolnego czworokąta wypukłego równe jest połowie pola równoległoboku wyznaczonego przez jego przekątne.
Dany jest równoległobok
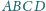 oraz punkt
oraz punkt
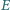 należący do boku
należący do boku
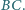 Przez punkt
Przez punkt
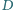 prowadzimy prostą
prowadzimy prostą
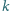 równoległą
do prostej
równoległą
do prostej
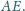 Na prostej
Na prostej
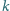 obieramy takie punkty
obieramy takie punkty
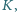
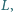 że czworokąt
że czworokąt
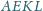 jest równoległobokiem. Udowodnij, że
równoległoboki
jest równoległobokiem. Udowodnij, że
równoległoboki
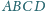 i
i
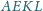 mają równe pola.
mają równe pola.
Punkt
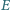 należy do boku
należy do boku
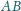 równoległoboku
równoległoboku
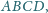 punkt
punkt
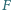 – do boku
– do boku
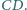 Odcinki
Odcinki
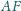 i
i
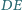 przecinają się w punkcie
przecinają się w punkcie
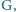 odcinki
odcinki
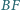 i
i
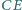 przecinają się w punkcie
przecinają się w punkcie
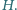 Wykaż,
że
Wykaż,
że

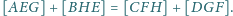
Na okręgu wybrano skończoną liczbę punktów i niektóre z nich oznaczono kolorem białym, a pozostałe czerwonym tak, że punktów białych jest przeszło dwukrotnie więcej niż czerwonych. Dowieść, że istnieje taki punkt biały, że każdy łuk okręgu, mający koniec w tym punkcie, zawiera więcej punktów białych niż czerwonych.
Dwusieczne kątów wewnętrznych trójkąta
 przecinają okrąg na nim
opisany odpowiednio w punktach
przecinają okrąg na nim
opisany odpowiednio w punktach
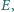
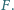 Odcinki prostych
Odcinki prostych
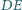 i
i
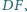 wyznaczone przez punkty przecięcia tych prostych
z bokami trójkąta, mają środki w punktach
wyznaczone przez punkty przecięcia tych prostych
z bokami trójkąta, mają środki w punktach
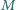 i
i
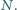 Odcinki
Odcinki
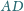 i
i
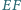 przecinają się w punkcie
przecinają się w punkcie
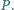 Wykazać, że
środek okręgu, przechodzącego przez punkty
Wykazać, że
środek okręgu, przechodzącego przez punkty
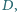
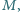
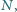 leży
na okręgu, przechodzącym przez punkty
leży
na okręgu, przechodzącym przez punkty
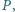
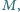
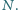
Zadanie 676 zaproponował pan Tomasz Ordowski
W trójkącie o bokach długości
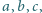 o wszystkich kątach
wewnętrznych mniejszych od
o wszystkich kątach
wewnętrznych mniejszych od
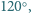 znajduje się punkt, którego suma
odległości od wierzchołków jest minimalna i wynosi
znajduje się punkt, którego suma
odległości od wierzchołków jest minimalna i wynosi
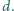 Dowieść,
że zachodzi równość
Dowieść,
że zachodzi równość
