Odpowiedź: nie.
Uzasadnienie: długość krzywej to kres górny długości linii łamanych w nią wpisanych. Weźmy więc dowolną łamaną, wpisaną w rozważaną krzywą (utworzoną dla pewnego parametru 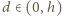 ); jej wierzchołki
); jej wierzchołki 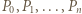 leżą (w takim porządku) na owej krzywej, przy czym
leżą (w takim porządku) na owej krzywej, przy czym 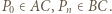 Przedłużenia odcinków
Przedłużenia odcinków 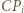 docierają do boku
docierają do boku 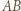 w punktach
w punktach 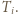 Ustalmy
Ustalmy 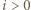 i spójrzmy na czworokąt
i spójrzmy na czworokąt 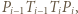 którego boki
którego boki 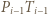 oraz
oraz 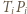 mają długość
mają długość 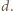 Przyjmijmy, że punkt
Przyjmijmy, że punkt 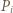 jest nie mniej oddalony od prostej
jest nie mniej oddalony od prostej 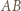 niż punkt
niż punkt 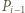 (gdy jest przeciwnie, zamieniamy role wskaźników
(gdy jest przeciwnie, zamieniamy role wskaźników 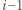 oraz
oraz 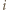 ). Niech punkt
). Niech punkt 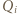 uzupełnia równoległobok
uzupełnia równoległobok 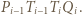 Skoro półproste
Skoro półproste 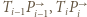 spotykają się (w punkcie
spotykają się (w punkcie 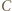 ), odcinek
), odcinek 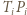 przecina odcinek
przecina odcinek 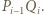 Trójkąt
Trójkąt 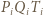 jest równoramienny, jego osią symetrii jest symetralna odcinka
jest równoramienny, jego osią symetrii jest symetralna odcinka 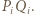 Punkt
Punkt 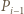 leży po tej stronie owej symetralnej co punkt
leży po tej stronie owej symetralnej co punkt 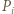 - zatem bliżej punktu
- zatem bliżej punktu 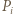 niż punktu
niż punktu 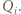 Tak więc
Tak więc 
Taka nierówność zachodzi dla wszystkich 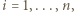 wobec czego łamana
wobec czego łamana 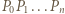 jest krótsza niż bok
jest krótsza niż bok 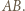 Biorąc kres górny długości wszystkich takich łamanych, wpisanych w rozważaną krzywą, stwierdzamy, że jej długość nie przekracza długości boku
Biorąc kres górny długości wszystkich takich łamanych, wpisanych w rozważaną krzywą, stwierdzamy, że jej długość nie przekracza długości boku 
[Korzystając ze wzoru całkowego na długość krzywej (najwygodniej we współrzędnvch biegunowych ze środkiem 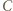 ), nietrudno się przekonać, że długość badanej krzywej jest ściśle malejącą funkcją parametru
), nietrudno się przekonać, że długość badanej krzywej jest ściśle malejącą funkcją parametru 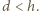 Dla
Dla 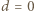 ta krzywa to odcinek
ta krzywa to odcinek 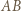 ; dla
; dla 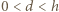 jej długość jest więc ostro mniejsza niż
jej długość jest więc ostro mniejsza niż 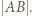 ]
]
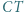 jest wysokością trójkąta
jest wysokością trójkąta 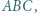 w którym
w którym 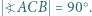 Okrąg o środku
Okrąg o środku 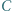 i promieniu
i promieniu 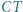 oraz okrąg opisany na trójkącie
oraz okrąg opisany na trójkącie 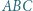 przecinają się w punktach
przecinają się w punktach 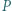 i
i 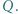 Dowieść, że prosta
Dowieść, że prosta 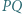 przechodzi przez środek odcinka
przechodzi przez środek odcinka 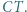
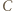 ma równą potęgę względem obu okręgów z zadania. Umiejętne zastosowanie twierdzenia Pitagorasa powinno wystarczyć.
ma równą potęgę względem obu okręgów z zadania. Umiejętne zastosowanie twierdzenia Pitagorasa powinno wystarczyć.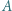 poprowadzono styczne do okręgu
poprowadzono styczne do okręgu 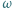 o środku
o środku 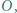 w punktach
w punktach 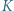 i
i 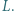 Punkt
Punkt 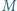 jest środkiem odcinka
jest środkiem odcinka 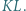 Okrąg
Okrąg 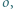 przechodzący przez punkty
przechodzący przez punkty 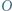 i
i 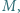 przecina okrąg
przecina okrąg 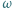 w punktach
w punktach 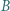 i
i 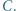 Wykazać, że punkty
Wykazać, że punkty 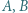 i
i 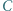 leżą na jednej prostej.
leżą na jednej prostej.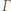 będzie okręgiem o średnicy
będzie okręgiem o średnicy 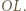 Wówczas okrąg
Wówczas okrąg 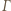 przechodzi przez punkt
przechodzi przez punkt 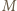 i jest styczny do prostej
i jest styczny do prostej 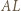 w punkcie
w punkcie 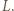 Wystarczy zauważyć, że punkt
Wystarczy zauważyć, że punkt 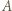 ma jednakową potęgę względem okręgów
ma jednakową potęgę względem okręgów 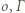 i
i 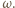
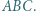 Okrąg styczny do odcinków
Okrąg styczny do odcinków 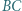 i
i 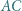 przecina odcinek
przecina odcinek 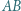 w punktach
w punktach 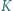 i
i 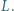 Wykazać, że
Wykazać, że 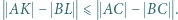
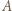 i
i 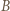 względem okręgu z zadania i odjąć stronami otrzymane równości.
względem okręgu z zadania i odjąć stronami otrzymane równości.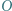 jest środkiem okręgu opisanego, a punkt
jest środkiem okręgu opisanego, a punkt 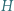 ortocentrum trójkąta ostrokątnego i różnobocznego
ortocentrum trójkąta ostrokątnego i różnobocznego 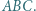 Punkty
Punkty 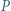 i
i 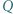 leżą odpowiednio na odcinkach
leżą odpowiednio na odcinkach 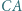 i
i 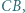 przy czym czworokąt
przy czym czworokąt 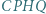 jest równoległobokiem. Wykazać, że
jest równoległobokiem. Wykazać, że 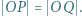
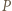 i
i 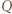 mają równą potęgę względem okręgu opisanego na trójkącie
mają równą potęgę względem okręgu opisanego na trójkącie 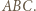 Do tego celu wystarczy podobieństwo odpowiednich trójkątów.
Do tego celu wystarczy podobieństwo odpowiednich trójkątów.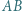 i prostopadła do niej cięciwa
i prostopadła do niej cięciwa 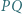 okręgu
okręgu  przecinają się w punkcie
przecinają się w punkcie 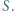 Okrąg
Okrąg 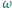 jest styczny (wewnętrznie) do okręgu
jest styczny (wewnętrznie) do okręgu  i do odcinków
i do odcinków 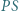 oraz
oraz 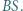 Niech
Niech 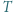 będzie punktem styczności okręgu
będzie punktem styczności okręgu 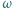 do odcinka
do odcinka 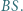 Wykazać, że
Wykazać, że 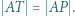
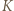 i
i 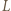 będą punktami styczności okręgu
będą punktami styczności okręgu 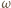 do, odpowiednio, okręgu
do, odpowiednio, okręgu  i odcinka
i odcinka 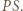 Wówczas punkty
Wówczas punkty 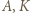 i
i 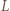 są współliniowe, gdyż punkt
są współliniowe, gdyż punkt 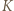 jest obrazem punktu
jest obrazem punktu 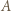 w jednokładności względem punktu
w jednokładności względem punktu 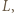 która przekształca okrąg
która przekształca okrąg  na
na 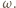 Mamy też
Mamy też 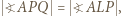 bo są to kąty wpisane, oparte na równej długości łukach okręgu
bo są to kąty wpisane, oparte na równej długości łukach okręgu  Resztę załatwia podobieństwo trójkątów i potęga punktu
Resztę załatwia podobieństwo trójkątów i potęga punktu 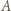 względem okręgu
względem okręgu 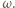
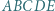 jest wpisany w okrąg o środku
jest wpisany w okrąg o środku 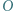 ; przy tym
; przy tym 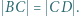 Przekątne
Przekątne 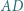 i
i 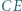 są prostopadłe, zaś przekątne
są prostopadłe, zaś przekątne 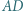 i
i 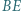 przecinają się w takim punkcie
przecinają się w takim punkcie 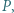 że
że  Wykazać, że trójkąt
Wykazać, że trójkąt  jest równoboczny.
jest równoboczny.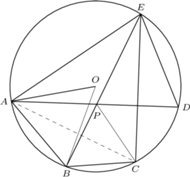
 punkt
punkt 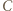 jest środkiem łuku
jest środkiem łuku 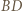 ; zatem prosta
; zatem prosta 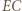 jest dwusieczną kąta wpisanego
jest dwusieczną kąta wpisanego 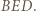 Przy tym jest prostopadła do prostej
Przy tym jest prostopadła do prostej 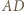 ; jest więc symetralną odcinka
; jest więc symetralną odcinka 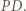 Stąd wynika, że
Stąd wynika, że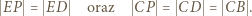
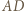 i
i 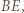 przecinające się w punkcie
przecinające się w punkcie 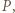 wyznaczają trójkąty podobne:
wyznaczają trójkąty podobne: 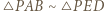 ; a ponieważ
; a ponieważ 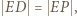 zatem
zatem 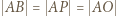 (ostatnia równość jest dana w założeniach). To pokazuje, że trójkąt
(ostatnia równość jest dana w założeniach). To pokazuje, że trójkąt 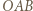 jest równoboczny, wobec czego
jest równoboczny, wobec czego 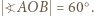 W takim razie
W takim razie 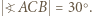
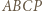 to deltoid
to deltoid 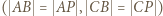 ; stąd
; stąd 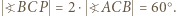 Wobec wcześniejszego spostrzeżenia, że
Wobec wcześniejszego spostrzeżenia, że 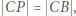 dostajemy tezę zadania: trójkąt
dostajemy tezę zadania: trójkąt 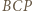 jest równoboczny.
jest równoboczny.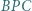 i
i 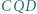 są równoboczne i leżą na zewnątrz równoległoboku
są równoboczne i leżą na zewnątrz równoległoboku 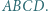 Udowodnić, że trójkąt
Udowodnić, że trójkąt 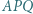 też jest równoboczny.
też jest równoboczny.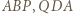 i
i 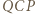 są przystające (bkb).
są przystające (bkb).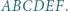 Punkty
Punkty 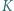 i
i 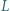 są środkami odcinków odpowiednio
są środkami odcinków odpowiednio 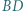 i
i 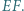 Dowieść, że trójkąt
Dowieść, że trójkąt 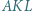 jest równoboczny.
jest równoboczny.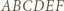 na
na  przystające trójkąty równoboczne można zauważyć, że odcinki
przystające trójkąty równoboczne można zauważyć, że odcinki 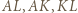 są dłuższymi przekątnymi przystających równoległoboków
są dłuższymi przekątnymi przystających równoległoboków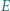 i
i 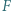 leżą odpowiednio na bokach
leżą odpowiednio na bokach 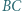 i
i 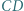 prostokąta
prostokąta 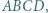 przy czym trójkąt
przy czym trójkąt 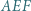 jest równoboczny. Punkt
jest równoboczny. Punkt 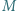 jest środkiem odcinka
jest środkiem odcinka 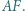 Wykazać, że trójkąt
Wykazać, że trójkąt 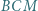 jest równoboczny.
jest równoboczny.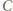 i
i 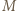 leżą na okręgu o średnicy
leżą na okręgu o średnicy 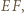 więc
więc 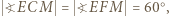 analogicznie
analogicznie 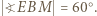
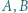 i
i 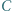 leżą kolejno na prostej
leżą kolejno na prostej 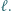 Punkty
Punkty 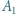 i
i 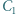 leżą po tej samej stronie prostej
leżą po tej samej stronie prostej 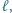 przy czym trójkąty
przy czym trójkąty 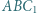 i
i 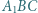 są równoboczne. Punkty
są równoboczne. Punkty 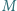 i
i 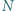 są środkami odcinków odpowiednio
są środkami odcinków odpowiednio 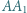 i
i 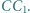 Udowodnić, że trójkąt
Udowodnić, że trójkąt 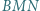 jest równoboczny.
jest równoboczny.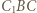 wokół punktu
wokół punktu 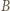 o
o 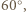 otrzymamy trójkąt
otrzymamy trójkąt 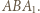 Obrazem punktu
Obrazem punktu 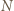 w tym obrocie jest punkt
w tym obrocie jest punkt 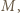 więc
więc 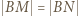 i
i 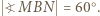
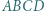 i punkt
i punkt 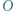 wewnątrz niego, przy czym zachodzą równości:
wewnątrz niego, przy czym zachodzą równości: 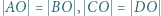 i
i 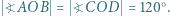 Dowieść, że środki odcinków
Dowieść, że środki odcinków 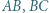 i
i 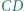 są wierzchołkami trójkąta równobocznego.
są wierzchołkami trójkąta równobocznego.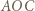 o
o 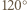 wokół punktu
wokół punktu  otrzymamy trójkąt
otrzymamy trójkąt 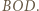 Zatem te trójkąty są przystające oraz proste
Zatem te trójkąty są przystające oraz proste 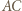 i
i 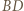 przecinają się pod kątem
przecinają się pod kątem 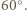
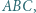 na zewnątrz niego, zbudowano trójkąty równoboczne
na zewnątrz niego, zbudowano trójkąty równoboczne 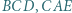 i
i 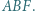 Środkami tych trójkątów są odpowiednio punkty
Środkami tych trójkątów są odpowiednio punkty 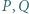 i
i 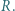 Dowieść, że trójkąt
Dowieść, że trójkąt 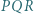 jest równoboczny (twierdzenie Napoleona).
jest równoboczny (twierdzenie Napoleona).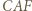 jest podobny do trójkąta
jest podobny do trójkąta 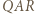 w skali
w skali 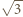 (bkb), analogicznie trójkąt
(bkb), analogicznie trójkąt 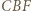 do
do 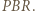 Stąd
Stąd 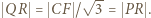 Tą samą metodą dowodzimy, że
Tą samą metodą dowodzimy, że 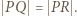
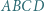 o podstawach
o podstawach 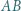 i
i 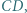 w którym
w którym 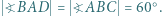 Na boku
Na boku 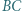 tego trapezu leży taki punkt
tego trapezu leży taki punkt 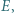 że
że 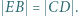 Wykazać, że
Wykazać, że 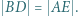
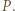 Wówczas trójkąty
Wówczas trójkąty 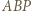 i
i 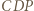 są równoboczne, dalej dowodzimy, że trójkąty
są równoboczne, dalej dowodzimy, że trójkąty 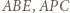 i
i 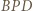 są przystające (bkb).
są przystające (bkb).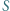 leży wewnątrz sześciokąta foremnego
leży wewnątrz sześciokąta foremnego 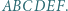 Udowodnić, że suma pól trójkątów
Udowodnić, że suma pól trójkątów 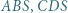 i
i 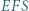 jest równa sumie pól trójkątów
jest równa sumie pól trójkątów 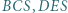 i
i 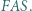
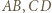 i
i 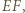 otrzymując trójkąt równoboczny. Suma pól trójkątów
otrzymując trójkąt równoboczny. Suma pól trójkątów 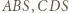 i
i 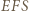 stanowi
stanowi 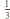 pola tego trójkąta.
pola tego trójkąta.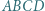 mamy
mamy 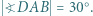 Wykazać, że
Wykazać, że 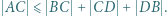
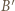 będzie punktem symetrycznym do
będzie punktem symetrycznym do 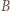 względem prostej
względem prostej 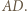 Wówczas trójkąt
Wówczas trójkąt 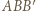 jest równoboczny oraz
jest równoboczny oraz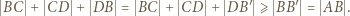
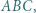 w którym
w którym 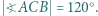 Punkt
Punkt 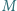 jest środkiem boku
jest środkiem boku 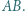 Na odcinkach
Na odcinkach 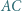 i
i 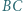 wybrano odpowiednio takie punkty
wybrano odpowiednio takie punkty 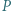 i
i 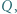 że
że 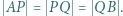 Wykazać, że
Wykazać, że 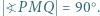
 będzie symetryczny do
będzie symetryczny do 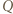 względem
względem 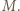 Wówczas trójkąt
Wówczas trójkąt 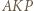 jest równoboczny.
jest równoboczny.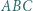 mamy
mamy 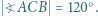 Punkty
Punkty 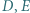 i
i 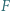 leżą na bokach odpowiednio
leżą na bokach odpowiednio 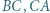 i
i 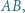 przy czym proste
przy czym proste 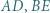 i
i 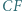 są dwusiecznymi kątów trójkąta
są dwusiecznymi kątów trójkąta 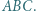 Udowodnić, że
Udowodnić, że 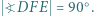
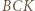 na zewnątrz trójkąta
na zewnątrz trójkąta 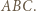 Wtedy
Wtedy 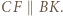 Korzystając z twierdzenia o dwusiecznej oraz podobieństwa trójkątów
Korzystając z twierdzenia o dwusiecznej oraz podobieństwa trójkątów 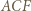 i
i 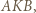 wykażemy, że
wykażemy, że 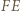 jest dwusieczną kąta
jest dwusieczną kąta 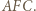 Analogicznie
Analogicznie 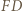 jest dwusieczną kąta
jest dwusieczną kąta 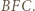
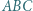 wybrano taki punkt
wybrano taki punkt 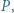 dla którego wartość wyrażenia
dla którego wartość wyrażenia 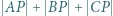 jest najmniejsza (punkt Fermata-Torricellego). Wykazać, że
jest najmniejsza (punkt Fermata-Torricellego). Wykazać, że 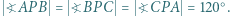
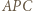 o
o 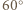 wokół punktu
wokół punktu 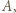 w kierunku zgodnym z orientacją trójkąta
w kierunku zgodnym z orientacją trójkąta 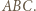 Otrzymamy trójkąt
Otrzymamy trójkąt 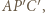 przystający do
przystający do 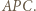 Trójkąt
Trójkąt 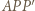 jest równoboczny, więc
jest równoboczny, więc 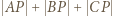 jest równe długości łamanej
jest równe długości łamanej 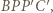 która jest najkrótsza, gdy jej wierzchołki są współliniowe.
która jest najkrótsza, gdy jej wierzchołki są współliniowe. Każdy bok i każdą przekątną
Każdy bok i każdą przekątną 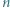 -kąta foremnego pomalowano przy użyciu jednego z
-kąta foremnego pomalowano przy użyciu jednego z  kolorów w taki sposób, że dla każdej trójki kolorów istnieje trójkąt o bokach w tych właśnie kolorach wyznaczony przez trzy spośród wierzchołków danego
kolorów w taki sposób, że dla każdej trójki kolorów istnieje trójkąt o bokach w tych właśnie kolorach wyznaczony przez trzy spośród wierzchołków danego 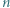 -kąta. Wykazać, że
-kąta. Wykazać, że 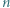 jest liczbą nieparzystą.
jest liczbą nieparzystą.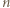 -kąta czadowym i zauważmy, że liczba czadowych trójkątów jest równa liczbie trójek kolorów. To oznacza, że jeśli warunki zadania są spełnione, to każda trójka kolorów pojawia się jako zbiór kolorów boków czadowego trójkąta dokładnie raz. W szczególności żaden czadowy trójkąt nie może mieć dwóch boków tego samego koloru.
-kąta czadowym i zauważmy, że liczba czadowych trójkątów jest równa liczbie trójek kolorów. To oznacza, że jeśli warunki zadania są spełnione, to każda trójka kolorów pojawia się jako zbiór kolorów boków czadowego trójkąta dokładnie raz. W szczególności żaden czadowy trójkąt nie może mieć dwóch boków tego samego koloru.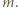 Z jednej strony liczba czadowych trójkątów o czerwonym boku jest równa
Z jednej strony liczba czadowych trójkątów o czerwonym boku jest równa 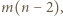 gdyż każdy czerwony odcinek jest bokiem dokładnie
gdyż każdy czerwony odcinek jest bokiem dokładnie 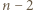 czadowych trójkątów. Z drugiej strony liczba ta jest równa liczbie sposobów doboru dwóch innych spośród
czadowych trójkątów. Z drugiej strony liczba ta jest równa liczbie sposobów doboru dwóch innych spośród  dostępnych kolorów do czerwonego, czyli
dostępnych kolorów do czerwonego, czyli 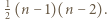 Stąd
Stąd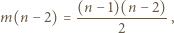
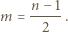
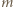 jest liczbą całkowitą, to
jest liczbą całkowitą, to 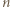 jest liczbą nieparzystą.
jest liczbą nieparzystą.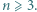 Każdy bok i każdą przekątną
Każdy bok i każdą przekątną 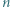 -kąta foremnego pomalowano przy użyciu jednego z
-kąta foremnego pomalowano przy użyciu jednego z  kolorów w taki sposób, że dwa odcinki mają ten sam kolor dokładnie wtedy, gdy są równoległe. Wykazać, że dla każdej trójki kolorów istnieje trójkąt o bokach w tych właśnie kolorach wyznaczony przez trzy spośród wierzchołków danego
kolorów w taki sposób, że dwa odcinki mają ten sam kolor dokładnie wtedy, gdy są równoległe. Wykazać, że dla każdej trójki kolorów istnieje trójkąt o bokach w tych właśnie kolorach wyznaczony przez trzy spośród wierzchołków danego 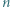 -kąta.
-kąta.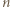 -kąta czadowym. Zauważmy, że skoro każde dwa jednokolorowe odcinki są równoległe, to każdy czadowy trójkąt ma różnokolorowe boki. Liczba trójek kolorów jest równa liczbie czadowych trójkątów, więc do rozwiązania zadania wystarczy wykazać, że każde dwa różne czadowe trójkąty mają różne zbiory kolorów boków.
-kąta czadowym. Zauważmy, że skoro każde dwa jednokolorowe odcinki są równoległe, to każdy czadowy trójkąt ma różnokolorowe boki. Liczba trójek kolorów jest równa liczbie czadowych trójkątów, więc do rozwiązania zadania wystarczy wykazać, że każde dwa różne czadowe trójkąty mają różne zbiory kolorów boków.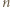 -kącie foremnym), to są przystające, a rozważana jednokładność jest symetrią względem środka tego okręgu. To jednak oznacza, że pewne dwa wierzchołki danego
-kącie foremnym), to są przystające, a rozważana jednokładność jest symetrią względem środka tego okręgu. To jednak oznacza, że pewne dwa wierzchołki danego 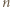 -kąta wyznaczają średnicę tego okręgu, co z kolei przeczy założeniu, że
-kąta wyznaczają średnicę tego okręgu, co z kolei przeczy założeniu, że 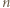 jest liczbą nieparzystą. Uzyskana sprzeczność kończy rozwiązanie zadania.
jest liczbą nieparzystą. Uzyskana sprzeczność kończy rozwiązanie zadania.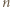 -kąta kolejnymi resztami z dzielenia przez
-kąta kolejnymi resztami z dzielenia przez 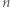 i zauważmy, że odcinki
i zauważmy, że odcinki 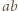 oraz
oraz 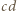 mają ten sam kolor wtedy i tylko wtedy, gdy
mają ten sam kolor wtedy i tylko wtedy, gdy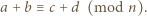
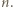
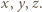 Trójkąt
Trójkąt 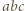 ma boki
ma boki 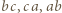 odpowiednio w tych kolorach wtedy i tylko wtedy, gdy
odpowiednio w tych kolorach wtedy i tylko wtedy, gdy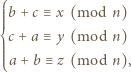
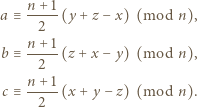
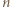 jest liczbą nieparzystą, więc trójka
jest liczbą nieparzystą, więc trójka 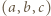 jest wyznaczona jednoznacznie z dokładnością do reszty z dzielenia przez
jest wyznaczona jednoznacznie z dokładnością do reszty z dzielenia przez 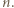
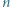 -kąta. Wykazać, że jego wierzchołki można tak pokolorować trzema kolorami, aby każde dwa punkty połączone bokiem lub jedną z narysowanych przekątnych miały różny kolor.
-kąta. Wykazać, że jego wierzchołki można tak pokolorować trzema kolorami, aby każde dwa punkty połączone bokiem lub jedną z narysowanych przekątnych miały różny kolor. -kąta (niekoniecznie wypukłego) nazywamy podział tego wielokąta na
-kąta (niekoniecznie wypukłego) nazywamy podział tego wielokąta na 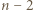 trójkąty przy użyciu pewnej liczby nieprzecinających się przekątnych (które mogą mieć wspólne końce).
trójkąty przy użyciu pewnej liczby nieprzecinających się przekątnych (które mogą mieć wspólne końce). -kąta o tej własności, że w każdym wierzchołku tego trójkąta schodzi się nieparzysta liczba trójkątów tej triangulacji. Wykazać, że
-kąta o tej własności, że w każdym wierzchołku tego trójkąta schodzi się nieparzysta liczba trójkątów tej triangulacji. Wykazać, że  jest liczbą podzielną przez 3.
jest liczbą podzielną przez 3. -kąta (niekoniecznie wypukłego) nazywamy podział tego wielokąta na
-kąta (niekoniecznie wypukłego) nazywamy podział tego wielokąta na 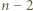 trójkąty przy użyciu pewnej liczby nieprzecinających się przekątnych (które mogą mieć wspólne końce).
trójkąty przy użyciu pewnej liczby nieprzecinających się przekątnych (które mogą mieć wspólne końce).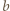 i
i 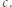
 -kąta należą do trójkątów triangulacji tego samego koloru; bez straty ogólności przypuśćmy, że jest to kolor czarny. Tymczasem każda przekątna triangulacji jest bokiem dokładnie jednego trójkąta czarnego i jednego trójkąta białego. Stąd wniosek, że łączna liczba narysowanych przekątnych jest równa
-kąta należą do trójkątów triangulacji tego samego koloru; bez straty ogólności przypuśćmy, że jest to kolor czarny. Tymczasem każda przekątna triangulacji jest bokiem dokładnie jednego trójkąta czarnego i jednego trójkąta białego. Stąd wniosek, że łączna liczba narysowanych przekątnych jest równa 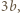 a łączna liczba boków
a łączna liczba boków  -kąta i narysowanych przekątnych jest równa
-kąta i narysowanych przekątnych jest równa 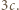 W konsekwencji
W konsekwencji 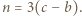
 -kąta, przy czym
-kąta, przy czym 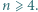 Na czarno malujemy wszystkie trójkąty tej triangulacji, których dokładnie jeden bok jest przekątną danego
Na czarno malujemy wszystkie trójkąty tej triangulacji, których dokładnie jeden bok jest przekątną danego  -kąta, a na biało - wszystkie trójkąty tej triangulacji, których wszystkie trzy boki są przekątnymi danego
-kąta, a na biało - wszystkie trójkąty tej triangulacji, których wszystkie trzy boki są przekątnymi danego  -kąta. Wykazać, że liczba czarnych trójkątów jest o
-kąta. Wykazać, że liczba czarnych trójkątów jest o 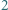 większa od liczby białych trójkątów.
większa od liczby białych trójkątów. -kąta (niekoniecznie wypukłego) nazywamy podział tego wielokąta na
-kąta (niekoniecznie wypukłego) nazywamy podział tego wielokąta na 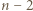 trójkąty przy użyciu pewnej liczby nieprzecinających się przekątnych (które mogą mieć wspólne końce).
trójkąty przy użyciu pewnej liczby nieprzecinających się przekątnych (które mogą mieć wspólne końce).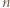 -kąta i oznaczmy przez
-kąta i oznaczmy przez 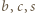 odpowiednio liczby białych, czarnych i szarych trójkątów.
odpowiednio liczby białych, czarnych i szarych trójkątów.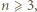 to nie istnieje trójkąt, którego wszystkie boki są także bokami danego
to nie istnieje trójkąt, którego wszystkie boki są także bokami danego  -kąta, więc każdy z
-kąta, więc każdy z 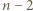 trójkątów został pomalowany dokładnie jednym kolorem, czyli
trójkątów został pomalowany dokładnie jednym kolorem, czyli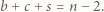
 -kąta, a każdy szary trójkąt ma dokładnie jeden taki bok. Stąd
-kąta, a każdy szary trójkąt ma dokładnie jeden taki bok. Stąd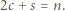
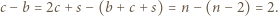
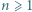 różnych okręgów dzieli płaszczyznę na co najwyżej
różnych okręgów dzieli płaszczyznę na co najwyżej 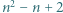 obszarów.
obszarów.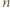 okręgów na płaszczyźnie, to po dorysowaniu jeszcze jednego liczba obszarów wzrośnie o co najwyżej
okręgów na płaszczyźnie, to po dorysowaniu jeszcze jednego liczba obszarów wzrośnie o co najwyżej 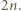
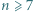 możemy tak umieścić w wierzchołkach
możemy tak umieścić w wierzchołkach  -kąta foremnego różne liczby od
-kąta foremnego różne liczby od 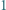 do
do 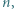 by wartość bezwzględna różnicy liczb z każdych dwóch sąsiednich wierzchołków była kwadratem liczby naturalnej.
by wartość bezwzględna różnicy liczb z każdych dwóch sąsiednich wierzchołków była kwadratem liczby naturalnej.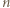 -kątów, w których
-kątów, w których 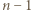 i
i 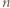 są przypisane sąsiednim wierzchołkom. Krok indukcji o głębokości
są przypisane sąsiednim wierzchołkom. Krok indukcji o głębokości 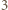 polega na dodaniu trzech wierzchołków z liczbami
polega na dodaniu trzech wierzchołków z liczbami 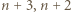 i
i 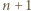 pomiędzy tymi dwoma.
pomiędzy tymi dwoma.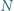 kwadratów o bokach równoległych i prostopadłych do ustalonego wspólnego kierunku. Niech
kwadratów o bokach równoległych i prostopadłych do ustalonego wspólnego kierunku. Niech 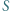 będzie zbiorem środków tych kwadratów; zakładamy, że jest to
będzie zbiorem środków tych kwadratów; zakładamy, że jest to 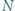 różnych punktów oraz że żaden punkt zbioru
różnych punktów oraz że żaden punkt zbioru 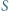 nie leży na brzegu żadnego kwadratu. Udowodnić, że można wyróżnić niektóre z tych
nie leży na brzegu żadnego kwadratu. Udowodnić, że można wyróżnić niektóre z tych 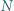 kwadratów tak, by każdy punkt zbioru
kwadratów tak, by każdy punkt zbioru 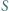 leżał w co najmniej jednym wyróżnionym kwadracie oraz w co najwyżej czterech wyróżnionych kwadratach.
leżał w co najmniej jednym wyróżnionym kwadracie oraz w co najwyżej czterech wyróżnionych kwadratach.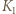 będzie największym spośród
będzie największym spośród 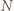 kwadratów (jeśli jest kilka przystających, większych od pozostałych, wybieramy dowolny). Niech
kwadratów (jeśli jest kilka przystających, większych od pozostałych, wybieramy dowolny). Niech 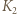 będzie największym spośród tych, których środki nie leżą w
będzie największym spośród tych, których środki nie leżą w 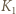 ; itd. (indukcja): niech
; itd. (indukcja): niech 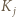 będzie największym spośród tych, których środki nie leżą w
będzie największym spośród tych, których środki nie leżą w 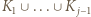 ; gdy takich kwadratów już nie ma, kończymy numerowanie. Ponumerowane kwadraty
; gdy takich kwadratów już nie ma, kończymy numerowanie. Ponumerowane kwadraty 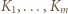 będą tymi "wyróżnionymi". Zbiór
będą tymi "wyróżnionymi". Zbiór 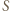 zawiera się w
zawiera się w 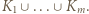 Przy tym środek żadnego wyróżnionego kwadratu nie leży w żadnym innym wyróżnionym kwadracie.
Przy tym środek żadnego wyróżnionego kwadratu nie leży w żadnym innym wyróżnionym kwadracie.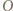 któregokolwiek spośród pozostałych kwadratów leży w co najmniej pięciu wyróżnionych kwadratach. Przyjmujemy punkt
któregokolwiek spośród pozostałych kwadratów leży w co najmniej pięciu wyróżnionych kwadratach. Przyjmujemy punkt 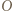 za początek układu współrzędnych
za początek układu współrzędnych 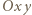 o osiach równoległych do boków kwadratów (jednostkę długości wybieramy dowolnie). Osie dzielą płaszczyznę na cztery ćwiartki, więc pewne dwa wyróżnione kwadraty
o osiach równoległych do boków kwadratów (jednostkę długości wybieramy dowolnie). Osie dzielą płaszczyznę na cztery ćwiartki, więc pewne dwa wyróżnione kwadraty 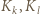 (zawierające
(zawierające 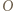 ) mają środki
) mają środki 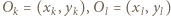 położone w jednej ćwiartce. Bez straty ogólności przyjmijmy, że
położone w jednej ćwiartce. Bez straty ogólności przyjmijmy, że 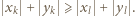 Wówczas
Wówczas 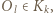 wbrew wcześniejszemu spostrzeżeniu. Sprzeczność kończy dowód.
wbrew wcześniejszemu spostrzeżeniu. Sprzeczność kończy dowód.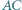 i
i 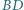 przecinają się w punkcie
przecinają się w punkcie 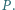 Wykazać, że
Wykazać, że![√ --------- √ ------- √ ------- [ABCD] ⩾ [ABP + [CDP ,](/math/temat/matematyka/geometria/planimetria/zadania/2019/04/30/zm-1602/4x-6f30022e90be6b8372c582cf70ce78e46db1ae4d-dm-2C,6B,73-FF,FF,FF.gif)
![[ℱ]](/math/temat/matematyka/geometria/planimetria/zadania/2019/04/30/zm-1602/5x-6f30022e90be6b8372c582cf70ce78e46db1ae4d-im-2C,6B,73-FF,FF,FF.gif) oznacza pole figury
oznacza pole figury 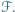
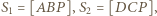
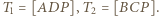 Zauważmy, że
Zauważmy, że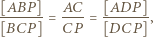
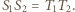 Wobec tego przekształcając równoważnie dowodzoną nierówność, mamy
Wobec tego przekształcając równoważnie dowodzoną nierówność, mamy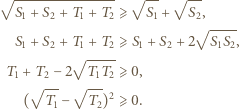
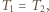 czyli gdy
czyli gdy 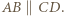
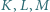 leżą odpowiednio na bokach
leżą odpowiednio na bokach 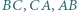 trójkąta
trójkąta 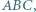 przy czym
przy czym
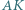 i
i 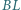 przecinają się w punkcie
przecinają się w punkcie 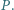 Wykazać, że punkty
Wykazać, że punkty 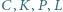 leżą na jednym okręgu.
leżą na jednym okręgu.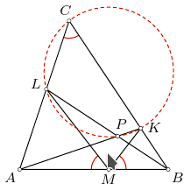
 oraz
oraz 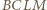 można opisać okręgi. Wobec tego
można opisać okręgi. Wobec tego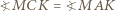
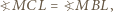
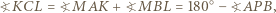
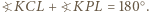
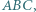 w którym wysokość opuszczona z wierzchołka
w którym wysokość opuszczona z wierzchołka 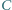 ma długość
ma długość 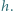 Na każdym odcinku
Na każdym odcinku 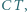 łączącym wierzchołek
łączącym wierzchołek 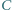 z bokiem
z bokiem 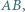 odkładamy odcinek
odkładamy odcinek 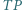 ustalonej długości
ustalonej długości 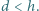 Uzyskane w ten sposób punkty
Uzyskane w ten sposób punkty 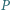 tworzą pewną krzywą. Czy - jeśli liczba
tworzą pewną krzywą. Czy - jeśli liczba 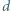 jest dostatecznie mała - długość owej krzywej przekroczy długość boku
jest dostatecznie mała - długość owej krzywej przekroczy długość boku 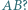
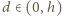 ); jej wierzchołki
); jej wierzchołki 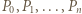 leżą (w takim porządku) na owej krzywej, przy czym
leżą (w takim porządku) na owej krzywej, przy czym 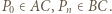 Przedłużenia odcinków
Przedłużenia odcinków 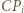 docierają do boku
docierają do boku 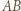 w punktach
w punktach 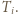 Ustalmy
Ustalmy 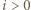 i spójrzmy na czworokąt
i spójrzmy na czworokąt 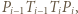 którego boki
którego boki 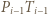 oraz
oraz 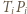 mają długość
mają długość 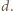 Przyjmijmy, że punkt
Przyjmijmy, że punkt 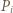 jest nie mniej oddalony od prostej
jest nie mniej oddalony od prostej 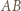 niż punkt
niż punkt 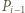 (gdy jest przeciwnie, zamieniamy role wskaźników
(gdy jest przeciwnie, zamieniamy role wskaźników 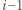 oraz
oraz 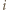 ). Niech punkt
). Niech punkt 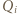 uzupełnia równoległobok
uzupełnia równoległobok 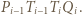 Skoro półproste
Skoro półproste 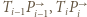 spotykają się (w punkcie
spotykają się (w punkcie 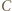 ), odcinek
), odcinek 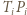 przecina odcinek
przecina odcinek 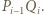 Trójkąt
Trójkąt 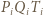 jest równoramienny, jego osią symetrii jest symetralna odcinka
jest równoramienny, jego osią symetrii jest symetralna odcinka 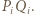 Punkt
Punkt 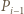 leży po tej stronie owej symetralnej co punkt
leży po tej stronie owej symetralnej co punkt 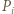 - zatem bliżej punktu
- zatem bliżej punktu 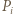 niż punktu
niż punktu 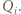 Tak więc
Tak więc 
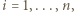 wobec czego łamana
wobec czego łamana 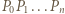 jest krótsza niż bok
jest krótsza niż bok 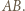 Biorąc kres górny długości wszystkich takich łamanych, wpisanych w rozważaną krzywą, stwierdzamy, że jej długość nie przekracza długości boku
Biorąc kres górny długości wszystkich takich łamanych, wpisanych w rozważaną krzywą, stwierdzamy, że jej długość nie przekracza długości boku 
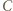 ), nietrudno się przekonać, że długość badanej krzywej jest ściśle malejącą funkcją parametru
), nietrudno się przekonać, że długość badanej krzywej jest ściśle malejącą funkcją parametru 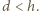 Dla
Dla 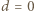 ta krzywa to odcinek
ta krzywa to odcinek 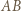 ; dla
; dla 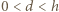 jej długość jest więc ostro mniejsza niż
jej długość jest więc ostro mniejsza niż 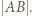 ]
] -kąta wypukłego nie przecinają się w jednym punkcie. Ile jest punktów przecięcia się przekątnych wewnątrz tego wielokąta?
-kąta wypukłego nie przecinają się w jednym punkcie. Ile jest punktów przecięcia się przekątnych wewnątrz tego wielokąta? -kąta należy dobrać w parę z czwórką (nieuporządkowaną) wierzchołków
-kąta należy dobrać w parę z czwórką (nieuporządkowaną) wierzchołków  -kąta, które są końcami tych przekątnych.
-kąta, które są końcami tych przekątnych.