Najkrótsza łamana»Zadanie 8
o zadaniu...
- Zadanie pochodzi z artykułu Najkrótsza łamana
- Publikacja w Delcie: styczeń 2012
- Publikacja elektroniczna: 01-01-2012
- Artykuł źródłowy w wersji do druku [application/pdf]: (84 KB)
Wykaż, że

Wykaż, że

Na płaszczyźnie dane są punkty
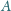 i
i
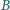 . Dany jest też kąt
skierowany
. Dany jest też kąt
skierowany
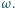 Przez
Przez
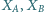 oznaczamy obraz punktu
oznaczamy obraz punktu
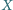 przy obrocie o kąt
przy obrocie o kąt
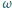 względem punktu
względem punktu
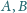 , odpowiednio.
Znaleźć wszystkie punkty
, odpowiednio.
Znaleźć wszystkie punkty
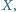 dla których trójkąt
dla których trójkąt
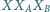 jest równoboczny.
jest równoboczny.
Wykaż, że w dowolnym czworokącie odcinki łączące środki przeciwległych boków oraz odcinek łączący środki przekątnych przecinają się w jednym punkcie.
Czworokąt
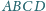 jest wpisany w okrąg o środku
jest wpisany w okrąg o środku
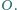 Przekątne
Przekątne
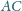 i
i
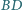 są prostopadłe i przecinają się w punkcie
są prostopadłe i przecinają się w punkcie
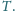 Udowodnij, że punkt przecięcia odcinków łączących środki
przeciwległych boków jest środkiem odcinka
Udowodnij, że punkt przecięcia odcinków łączących środki
przeciwległych boków jest środkiem odcinka
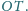
Punkty
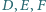 należą odpowiednio do boków
należą odpowiednio do boków
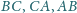 trójkąta
trójkąta
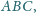 proste
proste
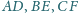 przecinają się w punkcie
przecinają się w punkcie
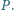 Wykaż,
że
Wykaż,
że
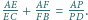
Okrąg
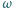 jest wpisany w romb
jest wpisany w romb
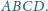 Prosta
Prosta
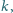 styczna do
okręgu
styczna do
okręgu
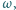 przecina odcinki
przecina odcinki
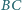 i
i
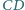 odpowiednio
w punktach
odpowiednio
w punktach
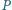 i
i
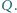 Wykaż, że wartość iloczynu
Wykaż, że wartość iloczynu
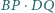 nie zależy od wyboru stycznej
nie zależy od wyboru stycznej
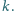
Czy dla dowolnego punktu
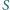 wewnątrz trójkąta można w jego
wierzchołkach umieścić takie masy, by ich środek ciężkości był w
wewnątrz trójkąta można w jego
wierzchołkach umieścić takie masy, by ich środek ciężkości był w
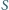 ?
?
Na płaszczyźnie danych jest sześć punktów, z których żadne trzy nie są
współliniowe. Środek ciężkości trójkąta utworzonego przez pewne trzy
z nich oznaczmy jako
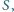 zaś środek ciężkości trójkąta utworzonego
przez pozostałe trzy – jako
zaś środek ciężkości trójkąta utworzonego
przez pozostałe trzy – jako
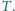 Wykaż, że wszystkie tak wyznaczone
proste
Wykaż, że wszystkie tak wyznaczone
proste
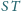 przecinają się w jednym punkcie.
przecinają się w jednym punkcie.
Wykaż, że wszystkie osie symetrii wielokąta przecinają się w jednym punkcie.
Trzy muchy o równych masach i zaniedbywalnych rozmiarach spacerują po obwodzie trójkąta, jedna z nich przeszła cały obwód. Wykaż, że jeśli środek ciężkości much nie zmienia położenia, to pokrywa się ze środkiem ciężkości trójkąta.
Wykaż, że środkowe trójkąta przecinają się w środku ciężkości jego wierzchołków.
Udowodnij, że środkiem ciężkości obwodu trójkąta jest środek okręgu wpisanego w trójkąt utworzony przez środki jego boków.
W wierzchołkach trójkąta ostrokątnego
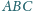 umieszczono masy
odpowiednio
umieszczono masy
odpowiednio
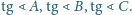 Wykaż, że ich środkiem
ciężkości jest ortocentrum
Wykaż, że ich środkiem
ciężkości jest ortocentrum
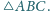
Zadanie zaproponował pan Tomasz Tkocz z Warszawy.
W trójkącie ostrokątnym o bokach długości
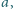
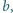
 środkowa
poprowadzona do boku
środkowa
poprowadzona do boku
 ma długość
ma długość
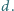 Wykazać, że dla
każdej liczby dodatniej
Wykazać, że dla
każdej liczby dodatniej
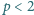 zachodzi nierówność
zachodzi nierówność

Udowodnić, że jeśli
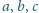 są długościami boków trójkąta, to
zachodzi nierówność
są długościami boków trójkąta, to
zachodzi nierówność
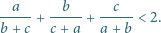
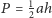
Punkt
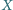 leży wewnątrz sześciokąta wypukłego
leży wewnątrz sześciokąta wypukłego
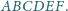 Punkty
Punkty
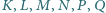 są odpowiednio
środkami boków
są odpowiednio
środkami boków
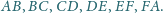 Wykaż, że
Wykaż, że
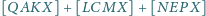 nie zależy od wyboru punktu
nie zależy od wyboru punktu
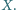
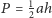
Dany jest czworokąt wypukły
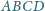 o polu 1. Punkt
o polu 1. Punkt
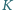 jest
symetryczny do punktu
jest
symetryczny do punktu
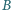 względem punktu
względem punktu
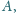 punkt
punkt
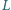 jest
symetryczny do punktu
jest
symetryczny do punktu
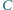 względem punktu
względem punktu
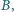 punkt
punkt
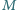 jest symetryczny do punktu
jest symetryczny do punktu
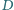 względem punktu
względem punktu
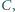 punkt
punkt
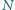 jest symetryczny do punktu
jest symetryczny do punktu
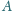 względem
punktu
względem
punktu
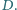 Oblicz
Oblicz
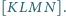
Udowodnij, że środkowe dzielą trójkąt na sześć trójkątów o równych polach.
Dany jest czworokąt wypukły
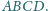 Punkty
Punkty
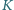 i
i
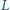 należą
do boku
należą
do boku
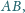 przy czym
przy czym
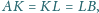 a punkty
a punkty
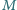 i
i
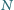 należą do boku
należą do boku
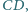 przy czym
przy czym
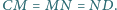 Wykaż,
że
Wykaż,
że
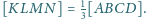
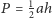
Dany jest taki pięciokąt wypukły
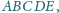 w którym pola trójkątów
w którym pola trójkątów
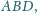
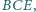
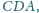
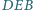 i
i
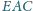 są równe.
Udowodnij, że każda przekątna tego pięciokąta jest równoległa do pewnego
jego boku.
są równe.
Udowodnij, że każda przekątna tego pięciokąta jest równoległa do pewnego
jego boku.
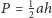
Każda z przekątnych
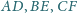 sześciokąta wypukłego
sześciokąta wypukłego
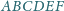 dzieli go na dwa czworokąty o równych polach. Wykaż, że
trójkąty
dzieli go na dwa czworokąty o równych polach. Wykaż, że
trójkąty
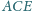 i
i
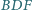 są podobne.
są podobne.
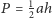
Dany jest czworokąt wypukły
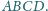 Punkty
Punkty
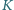 i
i
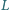 należą
odpowiednio do odcinków
należą
odpowiednio do odcinków
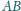 i
i
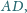 przy czym czworokąt
przy czym czworokąt
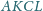 jest równoległobokiem. Odcinki
jest równoległobokiem. Odcinki
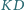 i
i
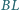 przecinają
się w punkcie
przecinają
się w punkcie
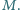 Wykaż, że
Wykaż, że
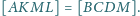
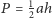
Przekątne czworokąta wypukłego
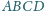 przecinają się w punkcie
przecinają się w punkcie
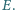 Wyznacz
Wyznacz
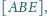 jeśli
jeśli
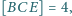
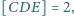
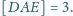
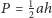
Przekątne trapezu
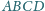 o podstawach
o podstawach
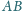 i
i
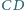 przecinają się
w punkcie
przecinają się
w punkcie
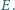 Dane są
Dane są
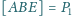 i
i
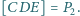 Wyznacz
Wyznacz
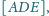
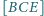 oraz
oraz