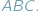Delta mi!

Najdłużej badanym problemem matematycznym była kwadratura koła. Zaraz za nią uplasowała się kwestia piątego postulatu Euklidesa. Chodziło o to, czy zdanie "jeśli dwie proste przecięte trzecią tworzą kąty wewnętrzne jednostronne o sumie mniejszej od dwóch kątów prostych, to proste te po przedłużeniu przetną się i to właśnie z tej strony" spełnia wymagane dla postulatów warunki, czyli czy wyraża rzeczy jasne i oczywiste i czy jest dostatecznie zwięzłe, by być uznane za pierwotną prawdę. Debatę zapoczątkował w V wieku Proklos, odpowiadając dwukrotnie nie i proponując, by wykazać, że usunięcie tego postulatu gmachu geometrii nie naruszy.

Tym razem o paraboli...

"Nie będziemy gadać niepotrzebnych rzeczy."

St.I. Witkiewicz, Szewcy, 1934

Wysokością czworokąta nazwijmy prostą przechodzącą przez środek jego boku i prostopadłą do boku przeciwległego. W niektórych czworokątach wszystkie cztery wysokości przecinają się w jednym punkcie - ortocentrum czworokąta. Przykładowo kwadrat ma ortocentrum, a romb niebędący kwadratem nie ma.

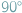W wielu zadaniach, w których występują kąty lub ich sumy, przydatne bywa przeniesienie pewnych figur tak, by kąty te znalazły się obok siebie. Szczególnie wygodne jest to wtedy, gdy suma pewnych kątów równa jest np. lub 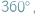a także, gdy niektóre z danych odcinków są równej długości.

Geometrzy od dawna marzyli o współrzędnych jednorodnych, czyli takich -tkach liczb (dalej dla uproszczenia będzie mowa o parach i trójkach) przyporządkowanych punktom, że gdy wszystkie liczby w 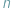-tce pomnożymy przez tę samą liczbę, to nowa 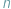-tka będzie współrzędnymi tego samego punktu.

W tym artykule omówimy pewną bardzo pożyteczną technikę - tzw. przesuwanie. Polega ona na tym, że niektóre obiekty przesuwamy o pewien wektor i udowadniamy, że teza zadania jest niezmiennicza ze względu na wykonanie tej operacji. Ta metoda pozwala na sprowadzenie rozwiązywanego zadania do znacznie prostszego. Bardzo często ten prostszy przypadek ma jakiś rodzaj symetrii, z której łatwo wywnioskować tezę. Zanim przejdziemy do rozwiązywania zadań, odnotujmy dwie proste własności opisanej operacji.

W poprzednim numerze przedstawiliśmy cykl wzajemnie wpisanych trójkątów i dwa wzajemnie wpisane pięciokąty. To było na płaszczyźnie. A teraz będzie przykład wzajemnego wpisania w przestrzeni trójwymiarowej.

Dawno, dawno temu żył sobie beztrosko król wraz ze swoją piękną córką. Jak to czasem w zbyt szczęśliwych królestwach bywa, pewnego razu czarnoksiężnik przybył na dwór, żeby porwać królewnę i uwięzić ją w swojej upiornej wieży. Zgodnie z zasadami dobrego wychowania mrocznych czarodziei, do których należał, musiał dać mieszkańcom królestwa możliwość ocalenia królewny przed swoim niecnym planem...

Tzw. zagadnienie Fermata to pytanie o to, gdzie wewnątrz danego trójkąta należy umieścić punkt 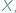aby suma długości odcinków 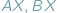i 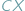przyjęła najmniejszą wartość.

W geometrii dyskretnej przyjęło się mówić, że wielokąt jest wpisany w inny wielokąt, gdy ma wierzchołki na prostych zawierających boki tego drugiego wielokąta. Od czasu Hilberta tego zwrotu używa się i w przypadku "zwyczajnej" geometrii.

...z których żadne dwie nie są równoległe, a żadne trzy nie mają punktu wspólnego... tworzą cztery trójkąty - to każdy widzi i nikt się nie dziwi.

Oto kilka zadań związanych z istnieniem i własnościami pewnych krzywych lub łamanych na płaszczyźnie i w przestrzeni trójwymiarowej.

- Lolek, chodź, pokażę Ci jedną stronę w Internecie...

W LXVIII Olimpiadzie Matematycznej uczestniczyło 1495 uczniów, zatem o 324 osoby więcej niż rok wcześniej, do zawodów stopnia drugiego zakwalifikowano 632 uczniów, a do zawodów stopnia trzeciego - 154 uczniów. Zapewne wynika to z pojawienia się w pierwszym stopniu sporej liczby zadań stosunkowo łatwych, a już na pewno niewymagających szczególnego przygotowania...

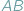Odcinek widać z punktu 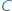pod kątem 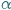, gdy 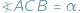Z twierdzenia o kątach wpisanych wynika, że jeśli punkty 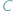i 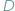leżą na okręgu po tej samej stronie jego cięciwy 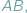to widać ją z 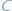i 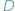pod tym samym kątem (Rys. 1).

Astrofizycy ostatnio twierdzą, że "Wszechświat jest płaski", co w ich żargonie oznacza, iż średnia krzywizna Wszechświata jest równa zeru (i tylko lokalnie jest zakłócana przez grawitację). Jeśli mają rację, to matematyka dowodzi, że Wszechświat przyjmuje jeden z 18 możliwych kształtów.

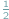Każdy zna twierdzenie o kącie zewnętrznym trójkąta: jest on równy sumie kątów wewnętrznych do niego nie przyległych (Rys. 1), co bierze się z faktu, że suma kątów przyległych jest równa sumie kątów trójkąta. Z twierdzenia tego wynika nietrudno twierdzenie o kącie wpisanym i środkowym: kąt wpisany jest równy kąta środkowego opartego na tym samym łuku.

Fakt (*). W trójkącie prostokątnym środek przeciwprostokątnej jest równo odległy od wierzchołków. Również na odwrót, jeśli środek okręgu opisanego leży na boku trójkąta, to trójkąt ten jest prostokątny.

Drogi Czytelniku, jeśli popatrzysz na płatki śniegu, to zobaczysz wielką ich rozmaitość. Bogactwo znanych kolekcji zdjęć śnieżynek mówi nam, że nie ma dwóch identycznych płatków śniegu. Możesz zapytać, czy możemy skatalogować pokrój kryształków lodu i wyjaśnić ich kształt?

Znam takie zadanie. Jego autorem jest Igor Fiodorowicz Szarygin. Jego treść jest nieskomplikowana: jak szeroki walec można włożyć pomiędzy trzy jednakowe, parami prostopadłe walce?

Jeśli chcemy wyznaczyć długość pewnej krzywej lub łamanej, często warto ją rozwinąć albo w inny sposób rozprostować.

Zabawmy się Pitagorasem, budując ustrojstwo przedstawione obok...

Dany jest okrąg...

W IV wieku przed naszą erą za sprawą Platona panowało powszechne przekonanie, że sfera niebieska - jako doskonała - dopuszcza jedynie doskonałe ruchy planet, jedynych ruchomych obiektów na niej. Ruchy doskonałe to ruchy jednostajne i odbywające się po doskonałych trajektoriach. Doskonała trajektoria to taka, która może ślizgać się po sobie - na sferze tę własność mają tylko okręgi. Powstawał więc problem, jak wytłumaczyć nieregularności ruchu planet na niebie, a w szczególności powstawanie pętli, o jakich jest mowa w artykule Tomasza Kwasta.

Gdy na lustrzaną sferę pada promień światła, odbija się on tak, że kąt między nim a przedłużeniem promienia sfery przechodzącego przez punkt, w którym promień pada, jest równy kątowi między tym przedłużeniem a promieniem odbitym, przy czym wszystko odbywa się w jednej płaszczyźnie wyznaczonej przez padający promień i środek sfery. Geometrycznie sytuacja jest więc dwuwymiarowa.

Prawie każdy wielościan ma talię (to wśród nich jest nawet częstsze niż u ludzi!), czyli pewien jego płaski przekrój ma obwód mniejszy od sąsiednich (dokładniej: niewielka zmiana płaszczyzny tnącej daje wielokąt o większym obwodzie - a bardziej po ludzku: nałożona w takim miejscu gumka recepturka nie zsunie się). Dla sześcianu taką talią jest jego przekrój będący sześciokątem foremnym (narysuj ją!).

W dowolnym trójkącie odcinek łączący środki dwóch boków jest równoległy do trzeciego boku i dwukrotnie od niego krótszy. Ten prosty fakt okazuje się zadziwiająco przydatny.

O kolorowaniu płaszczyzny raz jeszcze...

Chciałbym opowiedzieć o najtrudniejszym pojęciu matematyki. Najtrudniejszym, choć intuicyjnie prostym i używanym powszechnie również przez niematematyków. Chodzi o orientację...

Tym razem będziemy wycinać...

Twierdzenie Talesa dowieść można bez trudu...

Twierdzenie Pascala o równomiernym ciśnieniu gazu na ścianki naczynia pociąga za sobą twierdzenie Pitagorasa i jego uogólnienie, czyli twierdzenie kosinusów.

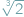Podwojenie sześcianu to zadanie: skonstruuj odcinek razy dłuższy od danego...

Cytat z General Relativity Johna Archibalda Wheelera, który został umieszczony u góry marginesu artykułu Michała Bejgera, można przejrzyście zilustrować geometrycznie, gdy zajmiemy się przestrzenią dwuwymiarową.

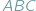Wyobraźmy sobie, że wewnątrz trójkąta umieściliśmy trójkąt 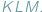Wówczas pole 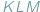nie przekracza, oczywiście, pola 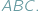Czy możemy stwierdzić to samo o obwodach tych trójkątów? W tym przypadku słowo "oczywiście" również wydaje się uprawnione, Czytelnicy Delty z pewnością wiedzą jednak, jak łatwo o nadużycie tej formułki. Szczęśliwie w tej sytuacji nie pociągałoby to za sobą tragicznych konsekwencji, gdyż istotnie, również obwód trójkąta 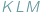nie przekracza obwodu trójkąta

W 1967 roku szkoła podstawowa wypuściła po raz pierwszy absolwentów ośmioletniej podstawówki (tak, kiedyś też były reformy szkolne). W ogólnym reformatorskim zamieszaniu można było zrobić coś nietypowego, więc Wydział Matematyki i Fizyki Uniwersytetu Warszawskiego uruchomił uniwersyteckie klasy matematyczno-fizyczne w liceum im. Klementa Gottwalda (w latach 1906-50 oraz po 1990 roku Stanisława Staszica) - pretekst był prosty: pierwszym dyrektorem tego liceum był Jan Zydler, znakomity nauczyciel matematyki i autor do dziś niezapomnianych podręczników geometrii.