Czarno-białe mapy
Słynne twierdzenie orzeka, że każdą mapę da się pomalować najwyżej czterema barwami. Oczywiście, zawsze należy malować tak, by sąsiadujące ze sobą państwa miały różne kolory. Są jednak mapy, dla których wystarczy mniej barw.
Słynne twierdzenie orzeka, że każdą mapę da się pomalować najwyżej czterema barwami. Oczywiście, zawsze należy malować tak, by sąsiadujące ze sobą państwa miały różne kolory. Są jednak mapy, dla których wystarczy mniej barw.
Panuje przekonanie, że w niemodnej obecnie dziedzinie geometrii klasycznej wszystko jest znane i nie pozostało nic do odkrycia. Kłam temu stwierdzeniu zadaje dość ciekawe i (jeszcze) mało znane twierdzenie, które przedstawiamy w niniejszym artykule. Warto zaznaczyć, że środki, jakie posłużyły nam do dowodu, są czysto geometryczne i nie korzystają z narzędzi analitycznych. Aby ułatwić jego zrozumienie, przedstawiamy najpierw pewne pojęcia, definicje i bardziej znane fakty powiązane z tym zagadnieniem.
Od Archimedesa wiemy, że zdaniem Demokryta stożek stanowi trzecią część walca, ale pierwszy udowodnił to Eudoksos. Znamy ten rezultat z XII Księgi Elementów Euklidesa (Stwierdzenie 10)...
W niniejszym artykule przybliżymy własności jednej z najsłynniejszych prostych w geometrii euklidesowej - prostej Simsona. Jej odkrycie przypisywane jest szkockiemu matematykowi, Robertowi Simsonowi, choć w żadnej jego pracy nie znajdujemy wzmianki o niej.
Wiele zadań przestrzennych łatwiej rozwiązać, gdy najpierw zbada się analogiczny problem płaski. Taki dwuwymiarowy odpowiednik czasem sam się narzuca, a czasem jego sformułowanie wymaga pewnej pomysłowości. Poniżej prezentujemy przykłady zadań o przestrzennych klockach, na różne sposoby "spłaszczane".
W artykule Czy Ziemia jest płaska (Delta 4/2016) pokazaliśmy, że sfera (będąca uproszczonym modelem powierzchni Ziemi) nie jest płaska, to znaczy nie daje się podzielić na fragmenty, z których każdy byłby izometryczny z pewnym fragmentem płaszczyzny. Przypomnijmy, że ta cecha odróżnia sferę od powierzchni bocznych walca i stożka. Pójdźmy więc dalej - czy jest możliwa taka gładka deformacja sfery, aby uzyskać powierzchnię płaską?

Euklides
(ok.365 p.n.e.-ok. 300 p.n.e.)
Geometrię szkolną nazywamy euklidesową, bo jej pierwsze aksjomaty zostały podane w Elementach Euklidesa (około -300). Wśród nich wyróżniał się aksjomat mówiący o tym, że na płaszczyźnie przez punkt poza prostą można poprowadzić tylko jedną prostą z nią rozłączną. Zasugerowana przez Proklosa (V wiek) możliwość wyprowadzenia tego aksjomatu z pozostałych przez następne 1300 lat drażniła ambicje praktycznie wszystkich matematyków, co owocowało dowodami błędnymi (bo opartymi na przesłankach, które same nie miały dowodów).
O zadaniu 16. z książki 100 zadań Steinhausa.
Wielościan wypukły, którego ściany są jednakowymi wielokątami foremnymi, może mieć ściany trójkątne, czworokątne lub pięciokątne. Ostatnie dwa przypadki realizują się tylko w postaci sześcianu i dwunastościanu...
Dwie nierównoległe płaszczyzny przecinają się wzdłuż prostej. Ta niepozorna obserwacja bywa bardzo przydatna.
Problem, który opiszę, został zaproponowany przez Amerykanów na LV Międzynarodową Olimpiadę Matematyczną, a jego treść brzmi następująco...
Gwiazdka foremna to łamana zamknięta, wpisana w okrąg i złożona z jednakowej długości cięciw, ale niebędąca wielokątem foremnym. Nie trzeba długo się zastanawiać, by stwierdzić, że odcinki takich łamanych muszą się przecinać.
Na pierwszym etapie XI Olimpiady Matematycznej Gimnazjalistów pojawiło się pytanie, na które tylko 24% uczestników odpowiedziało poprawnie...
Wiele przedmiotów zawdzięcza swe istnienie kompozycji dwóch pozornie niewspółistniejących ze sobą idei. Louis Braille połączył koncepcję zapisu graficznego, czyli odczytywanego za pomocą wzroku, ze sposobem zapisywania wiadomości zaprojektowanym dla ludzi niewidomych, którzy korzystają ze zmysłu dotyku. W rezultacie powstał alfabet dla niewidomych, który można odczytać także za pomocą wzroku. Podobnie narodził się pomysł na zbadanie obrazów inwersyjnych w różnych metrykach...

Mówi się, że origami powstało dwa tysiące lat temu wraz z wynalezieniem papieru. W tym kontekście wydaje się zaskakujące, że początek odkrywania matematyki stojącej za składaniem papieru przypada dopiero na lata osiemdziesiąte zeszłego stulecia. Dziś gałąź nauki zwana origami obliczeniowe (ang. computational origami) rozwija się bardzo prężnie.
Geometrie nieeuklidesowe Mała Delta
Czysty zeszyt, cyrkiel, linijka, kątomierz, liniuszek - standardowy szkolny ekwipunek lekcji geometrii. Ale istnieją również inne geometrie, w których do konstrukcji figur nie jest potrzebne żadne oprzyrządowanie. Jedną z nich jest geometria dziewięciu punktów, gdzie bez linijki czy cyrkla można "konstruować" całkiem dokładnie koła, trójkąty i inne figury.
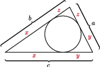
Jeśli w nierówności, którą chcemy uzasadnić, występują długości boków 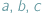 pewnego trójkąta, często przydaje się podstawienie Raviego:
pewnego trójkąta, często przydaje się podstawienie Raviego: 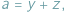
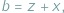
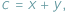 gdzie
gdzie 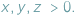 Takie liczby
Takie liczby 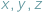 zawsze istnieją, są to bowiem długości odcinków stycznych do okręgu wpisanego w trójkąt.
zawsze istnieją, są to bowiem długości odcinków stycznych do okręgu wpisanego w trójkąt.
Euklides w Elementach pisał: "... kwadrat jest tym, co równoboczne i prostokątne...". Oto kilka niebanalnych obserwacji, w których kwadrat jest jednym z bohaterów.
Historia i filozofia nauk Nowości z przeszłości
Jak już pisałem (Delta 3/1979), metodę dedukcyjną i jej najdoskonalszą postać - metodę aksjomatyczną można wyprowadzić ze zwykłej praktyki dyskusji, niezmiernie rozpowszechnionych w starożytnej Grecji. Warto zobaczyć, co o strukturze pierwszego znanego nam aksjomatycznego wykładu matematyki -- Elementów Euklidesa może nam powiedzieć taka interpretacja.
W wielu zadaniach należy uzasadnić, że pewne trzy proste przecinają się w jednym punkcie. Często można wykazać, że wszystkie one są symetralnymi, dwusiecznymi, wysokościami albo środkowymi pewnego trójkąta, co oczywiście kończy dowód.
Chyba każdy patrzył kiedyś w kalejdoskop - prostokątne lustra odbijające różnobarwne wzory powstałe z przesypujących się koralików. Nie znam nikogo, kto mając w ręku owo urządzenie, byłby w stanie powstrzymać się przed choćby najmniejszym obróceniem nim i zerknięciem przez małe oczko na otrzymany efekt. A gdyby odwrócić sytuację i zbadać, jak zmieni się obraz, gdy zamiast koralikami poruszymy lustrami znajdującymi się w kalejdoskopie? Zacznijmy od wyprawy do szklarza i wyboru bohatera kalejdoskopowych przygód - po starannym castingu wygrywa żaba.
Stereometria Nowości z przeszłości
W 1752 roku znakomity matematyk szwajcarski Euler, podówczas profesor Akademii Nauk w Berlinie, odkrył zadziwiający związek między liczbami 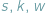 ścian, krawędzi i wierzchołków dowolnego wielościanu wypukłego
ścian, krawędzi i wierzchołków dowolnego wielościanu wypukłego 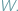 Związek ten jest obecnie nazywany wzorem Eulera dla wielościanów i zwykle zapisuje się go w postaci
Związek ten jest obecnie nazywany wzorem Eulera dla wielościanów i zwykle zapisuje się go w postaci

Podamy elementarny i chyba nader zabawny dowód tego wzoru.

Planimetria Nowości z przeszłości
Lecz wy się uczcie patrzeć, a nie gapić - B. Brecht
Skoro dwusieczna to półprosta dzieląca kąt na dwa równe kąty, to dlaczego dwusieczne kątów wewnętrznych każdego trójkąta przecinają się w jednym punkcie? Otóż...
Pozwolę sobie podtrzymać Czytelnika w napięciu i tytułowe pytanie tymczasem zostawię bez odpowiedzi. Zacznę za to od refleksji, czym jest płaskość.
Oznaczmy przez 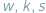 liczby odpowiednio wierzchołków, krawędzi i ścian wielościanu. W każdym wierzchołku schodzą się co najmniej trzy końce krawędzi i każda krawędź ma dwa końce, zatem
liczby odpowiednio wierzchołków, krawędzi i ścian wielościanu. W każdym wierzchołku schodzą się co najmniej trzy końce krawędzi i każda krawędź ma dwa końce, zatem 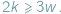 Podobnie każda ściana ma co najmniej trzy boki, a każda krawędź należy do dwóch ścian, więc
Podobnie każda ściana ma co najmniej trzy boki, a każda krawędź należy do dwóch ścian, więc 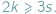 Ponadto jeśli wielościan jest wypukły, zachodzi wzór Eulera:
Ponadto jeśli wielościan jest wypukły, zachodzi wzór Eulera: 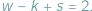
Chociaż są to pojęcia abstrakcyjne (bo przecież nikt nie widział ani punktu, ani odcinka), przemawiają dobrze do wyobraźni i zgadzają się ze zdrowym rozsądkiem. I aż dziw bierze, jak wiele wokół nas zjawisk, które zdają się ostrzegać: uwaga to co wydaje się takie oczywiste, wcale nie musi być prawdziwe.
Jednym z podstawowych wzorów trygonometrycznych jest twierdzenie kosinusów podające zależność między bokami trójkąta a jednym z jego kątów: 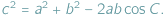 Na formułę tę można patrzeć jako na uogólnienie twierdzenia Pitagorasa (do którego sprowadza się, gdy kąt
Na formułę tę można patrzeć jako na uogólnienie twierdzenia Pitagorasa (do którego sprowadza się, gdy kąt 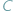 jest prosty, czyli
jest prosty, czyli 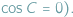

wikipedia
Alfred Tarski (1901-1983)
W artykule tym pragnę omówić pewne pojęcia, należące całkowicie do zakresu geometrii elementarnej, a dotąd niemal wcale nie zbadane. Jak wiadomo, dwa wielokąty 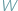 i
i 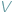 nazywamy równoważnymi, wyrażając to wzorem:
nazywamy równoważnymi, wyrażając to wzorem: 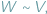 jezeli dają się one podzielić na jednakową ilość wielokątów odpowiednio przystających...
jezeli dają się one podzielić na jednakową ilość wielokątów odpowiednio przystających...

Gwoli precyzji ustalmy, że trzymając przed sobą zetknięte połówki przeciętej bryły obrotowej (prawą i lewą), obracamy prawą z nich ruchem do siebie.
Taka sobie niewinnie wyglądająca bryłka. Ot, powstała z obrotu kwadratu dookoła jego przekątnej, przecięcia tego, co powstało, na dwie identyczne części (wzdłuż płaszczyzny kwadratu), przekręceniu połowy o 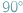 i doklejeniu do drugiej części (czekającej w tym czasie w bezruchu). Szczęśliwa całość - sferostożek (ang. sphericon).
i doklejeniu do drugiej części (czekającej w tym czasie w bezruchu). Szczęśliwa całość - sferostożek (ang. sphericon).

Dwunastościan gwiaździsty mały
Jeśli przy definiowaniu wielokąta zrezygnujemy z warunku, aby łamana tworząca go była zwyczajna, otrzymamy nową klasę wielokątów foremnych, tzw. gwiaździstych.
W ostatnich kilkunastu latach na pograniczu geometrii różniczkowej i teorii równań różniczkowych rozrósł się nowy, pokaźny dział matematyki, poświęcony badaniom krzywych i powierzchni, które poruszają się zgodnie z jakimś określonym przepisem, zmieniając wraz z upływem czasu swój charakter i własności. Różne punkty mogą przy tym poruszać się z różnymi prędkościami, wyznaczonymi przez rozmaite geometryczne charakterystyki krzywej czy powierzchni...
Rozpatrzmy dowolny trójkąt oraz cztery kwadraty zbudowane w sposób przedstawiony na rysunku 1. Wówczas zaznaczone kolorem trzy odcinki, łączące odpowiednie wierzchołki kwadratów oraz środek najniższego kwadratu, przecinają się w jednym punkcie.
Tym razem o obrotach na płaszczyźnie...
Niedawno podczas rozmowy z kolegami - młodymi matematykami i fizykami - zorientowałem się, że dla nich informacja o tym, jak wyglądają wszystkie możliwe ruchy obiektu materialnego w trójwymiarowej przestrzeni, jest zaskakująca...
Izometrią nazywamy przekształcenie, które nie zmienia odległości między punktami. Obrazy trzech niewspółliniowych punktów jednoznacznie ją wyznaczają. Twierdzenie Chaslesa głosi, że każda izometria płaszczyzny jest przesunięciem, obrotem lub symetrią z poślizgiem.

...a pięciokąt foremny można. Obok pokazana jest konstrukcja dziesięciokąta foremnego - kolorowy odcinek ma długość boku dziesięciokąta foremnego wpisanego w większy okrąg, a więc biorąc co drugi z wierzchołków takiego dziesięciokąta, otrzymamy pięciokąt foremny. Konstrukcja jest - jak widać - bardzo prosta. Ma tylko tę wadę, że nie wskazuje, jak konstruować inne wielokąty foremne.