Delta mi!

W wielu rysunkach bardzo pomocny jest sześcian, z narysowaniem którego raczej nie mamy problemu...

Którędy przebiega najkrótsza droga lotnicza z Warszawy do Vancouveru? Wbrew pozorom – mimo podobnej szerokości geograficznej – wcale nie wzdłuż równoleżnika, a nad Grenlandią, o czym łatwo się przekonać, naciągając nitkę na globusie.

Kontynuujemy opowieść o czworościanach równościennych – tym razem przyjrzymy się paru zadaniom z nimi związanym. Jakiś czas temu na konkursach matematycznych temat tych wdzięcznych czworościanów był dosyć modny...

Ortocentrum trójkąta to punkt przecięcia jego wysokości. Przyjmijmy oznaczenia jak na rysunkach 1 i 2 oraz założenie, że trójkąt  jest ostrokątny.

Trzy niewspółliniowe punkty na płaszczyźnie jednoznacznie wyznaczają okrąg, który przez nie przechodzi. Zatem jeśli pewne cztery punkty leżą na jednym okręgu, to jest to fakt godny odnotowania. W geometrii istnieje niezwykle urocze twierdzenie, które mówi, że aż dziewięć szczególnych punktów trójkąta leży na jednym okręgu.

Panuje przekonanie, że w nauczaniu matematyki powinno się eksponować fakt, że ma ona zastosowania. Gdy przyjrzeć się podręcznikom, a zwłaszcza testom kwalifikacyjnym, trudno oprzeć się wrażeniu, że są to rzeczy w stylu mierzenia wysokości piramidy za pomocą długości jej cienia i twierdzenia Talesa, lub też zadań w stylu: jeśli dwóch robotników kopie rów w ciągu 2 godzin, to ilu ich potrzeba, aby ten rów wykopać w 15 sekund? (odpowiedź: 1440).

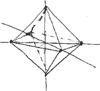
Kontynuujemy lekcje rysunku rozpoczęte w Delcie 6/2012. Kolejnym obiektem, który będziemy rysować, jest ośmiościan.

W poprzednim numerze Delty przedstawiłem trzy dowody V postulatu Euklidesa. Dla wszystkich Czytelników było jasne, że zawierają one błędy. Fakt, że mimo to każdy z nich przez pewien czas był uznany za poprawny, wskazuje na ogromny kłopot, jakim dla myślicieli – już niekoniecznie matematyków – było przyjęcie do wiadomości, że mogą istnieć dwie wykluczające się, ale poprawne, a więc w szczególności niesprzeczne teorie opisujące ten sam obiekt, w tym przypadku przestrzeń. A przecież przestrzeń, w której „odbywa się” Wszechświat, jest jedna.

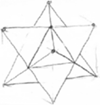
Wydaje się, że w czasach szybkich komputerów, programów graficznych i innych gadżetów nie ma sensu zajmowanie się rysunkiem odręcznym. Równie dobrze jednak można by zrezygnować z nauki pisania i tabliczki mnożenia – są przecież odpowiednie edytory i kalkulatory. Zdarza się jednak, że rozwiązując jakieś zadanie, dobrze byłoby podeprzeć naszą wyobraźnię właśnie rysunkiem, a nie ma pod ręką supernowoczesnych narzędzi.

W zawodach I stopnia obecnej, LXIII Olimpiady Matematycznej wzięło udział 1409 uczniów, więc nieco mniej niż w poprzedniej. Jest to liczba bliska wieloletniej średniej. Do drugiego stopnia zakwalifikowano 622 uczniów. Zawody drugiego stopnia odbyły się 17 i 18 lutego.

Przemieszczając się na płaszczyźnie za pomocą ruchów „do przodu”, „do tyłu”, „w lewo” i „w prawo”, możemy w szczególności narysować kwadrat. Czy analogiczna sytuacja rozważana na zakrzywionej powierzchni zawsze pozwala na wygenerowanie kwadratu przez zakreślaną trajektorię? Rozważmy sferę, którą często wykorzystuje się w globalnym modelowaniu powierzchni Ziemi.

Oczywiście, V postulatu Euklidesa nie da się dowieść na podstawie poprzednich czterech. Niemniej jednak praktycznie każdy znaczący matematyk od V do XIX wieku taki dowód przeprowadził i dopiero jego koledzy wskazywali, w którym miejscu rozumowania użył przesłanki z czterech początkowych postulatów niewynikającej...

Połączenie matematyki z religią może wydawać się nam, Europejczykom, dość zaskakujące. W Japonii jednak przez bardzo długi czas nie było niczym niezwykłym. Zjawisko to zostało zapoczątkowane w XVII wieku, kiedy władcy tego kraju podjęli decyzję o zamknięciu portów i odcięciu Japonii od reszty świata, szczególnie od Europy Zachodniej, a trwało do XIX wieku.

Od dwóch lat Fundacja Matematyków Wrocławskich oraz Instytut Matematyczny Uniwersytetu Wrocławskiego organizują konkurs matematycznego origami „Żuraw”. Mogą w nim startować uczniowie ze wszystkich typów szkół, a także dorośli amatorzy i profesjonalni matematycy. W odróżnieniu od innych konkursów origami w tym nie wystarczą zdolności manualne. W eliminacjach zawodnicy wykonują model matematyczny (płaski lub przestrzenny) w technice origami, natomiast w finale jest na odwrót – rozwiązują problemy dotyczące sztuki origami, używając technik matematycznych.

Poprzedni deltoid poświęcony był osiom potęgowym, między innymi twierdzeniu, które w skrócie brzmi tak: osie potęgowe trzech okręgów przecinają się w jednym punkcie. Ciekawym jego zastosowaniem jest dowód twierdzenia Brianchona.

7 stycznia 2012 roku około 1400 uczniów wzięło udział w drugim etapie VI Olimpiady Matematycznej Gimnazjalistów. Najciekawszym i jednocześnie najtrudniejszym zadaniem okazało się zadanie z planimetrii oznaczone numerem 5. Rozwiązało je niewielu uczniów, przy czym żaden z nich nie rozważył wszystkich możliwych konfiguracji. Poniżej postaramy się zadanie to dokładnie zanalizować.

Czy istnieje czworościan który nie jest foremny, a którego ściany są trójkątami przystającymi? Istnieje...

Na płaszczyźnie, jeśli trójkąt ma równe boki, to jest równoboczny. W przestrzeni jednak czworościan, którego ściany są przystające, wcale nie musi być foremny...

Nieco więcej o potędze punktu względem okręgu.

Czasem przydaje się do czegoś twierdzenie o dwusiecznej...

W Delcie 6/2011 Jerzy Zabczyk przytoczył anegdotę o Feynmanie w związku z pewnym geometrycznym zadaniem efektownie umieszczonym przez Hugona Steinhausa w Kalejdoskopie matematycznym (o czym Feynman nie wiedział) i zaproponował Czytelnikom atrakcyjne zadania.

Girard DESARGUES, matematyk, architekt ogrodów, doradca kardynała Richelieu (a więc rówieśnik Atosa, Portosa i Aramisa) postawił kolegom ogrodnikom pytanie: Jak posadzić 10 drzew w dziesięciu rzędach po 3 drzewa w każdym rzędzie?

Fleksagony to rodzina figur, które odpowiednio złożone z płaskiej kartki papieru mogą wskutek obracania pokazać nam cztery lub więcej „twarzy” (zamiast dwóch).

Niektóre nierówności, pozornie niezwiązane z geometrią, można zaskakująco łatwo udowodnić, wykorzystując twierdzenie Pitagorasa i prosty geometryczny fakt, że najkrótszą łamaną pomiędzy dwoma punktami jest łączący je odcinek.

Każdy, kto był w dżungli lub chociaż widział ją w jakimś filmie, wie, że poruszanie się po niej jest, delikatnie mówiąc, dosyć uciążliwe. Stanowi to ogromny kłopot szczególnie wtedy, gdy ktoś się w niej zgubi i chce się jakoś wydostać. Nie dość, że nie wiadomo, w jakim kierunku iść, to w ogóle ciężko jest nam pokonywać przeszkody (a rozwiązania siłowe, takie jak maczeta, niewiele dają). Istnieje następujące zalecenie: wystarczy znaleźć strumień (co zresztą wcale nie musi być łatwe), a potem liczyć na to, że zaprowadzi nas on do większej rzeki, a ta, być może, do morza.

Tematem poprzedniego deltoidu był środek ciężkości i związane z nim zadania. W tym numerze pora na zastosowania środka ciężkości w problemach pozornie z nim niezwiązanych. Na marginesie przypominamy podstawowe fakty.

W tym kąciku zajmiemy się pewnym zadaniem o czworościanie foremnym, o którym, między innymi, miałem okazję opowiadać na XLVI Szkole Matematyki Poglądowej pod hasłem Podejście niestandardowe.

Święta za pasem, więc przygotujmy się nieco do wieszania bombek na choince.

Środek ciężkości to – intuicyjnie – taki punkt, w którym trzeba coś podeprzeć, by owo coś utrzymało się w równowadze. Można go własnoręcznie poszukać na przykład dla długopisu, balansując nim poziomo na palcu.

Zasada Cavalieriego dla figur płaskich brzmi:
jeżeli dwie figury płaskie w przecięciu z każdą prostą równoległą do danej dają przekrój o tej samej długości, to pola tych figur są równe.

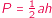
Najpopularniejszy wzór na pole trójkąta to jedna druga podstawa razy wysokość. Proste wnioski z tego wzoru pozwalają rozwiązać niełatwe czasem zadania.

W tym odcinku przyjrzymy się kątom dwuściennym. Jedną z najbardziej skutecznych metod radzenia sobie z nimi jest przeformułowanie problemu tak, żeby zamiast kątów dwuściennych pojawiły się kąty płaskie.

Zdarza się czasem, że zachód słońca i pusta, piaszczysta plaża zachwycają nas, kiedy patrzymy na nie, spacerując brzegiem morza, jednak zamknięte w martwe ramy zdjęcia przywodzą na myśl co najwyżej słowo „kicz”. Ta historia, gdyby jeden z hollyłódzkich reżyserów zdecydował się nakręcić film na jej podstawie, wydałaby się z pewnością banalna. Tymczasem napisało ją życie.

W poprzednim deltoidzie zaprezentowano kilka zadań z geometrii płaskiej, rozwiązanych poprzez „wyjście w przestrzeń”. Oto garść kolejnych przykładów na to, że warto płaskie rysunki postrzegać jako ilustracje sytuacji trójwymiarowych.

Niektóre zadania z geometrii płaskiej łatwiej najpierw rozwiązać w przestrzeni, a później dopiero z powrotem je „spłaszczyć”. Liczne przykłady pojawiły się w  deltoidach 17 i 18. Oto jeszcze dwa tego rodzaju problemy.

W grudniu 2010 roku ukazał się drugi tom serii wydawniczej Biblioteczka Stowarzyszenia na rzecz Edukacji Matematycznej zatytułowany Matematyka. Poszukuję – odkrywam. Materiały w nim zawarte stanowią opracowania referatów wygłoszonych w ramach konferencji Konkursy matematyczne w Polsce, zorganizowanej w 2008 roku przez Uniwersytet Warszawski we współpracy ze Stowarzyszeniem na rzecz Edukacji Matematycznej.

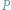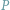Myślę, że niemal każdy Czytelnik miał okazję się z nią spotkać. Załóżmy, że mamy dany trójkąt, i wybierzmy dowolny punkt  z okręgu na nim opisanego. Wówczas rzuty prostokątne punktu  na proste zawierające boki danego trójkąta leżą na jednej prostej zwanej prostą Simsona.