Zadanie ZM-1421
o zadaniu...
- Publikacja w Delcie: maj 2014
- Publikacja elektroniczna: 01-05-2014
Udowodnić, że dla dodatnich liczb całkowitych
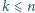 prawdziwa jest
nierówność
prawdziwa jest
nierówność
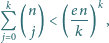
gdzie
 to stała zdefiniowana np. jako
to stała zdefiniowana np. jako
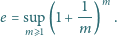
Udowodnić, że dla dodatnich liczb całkowitych
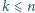 prawdziwa jest
nierówność
prawdziwa jest
nierówność
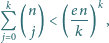
gdzie
 to stała zdefiniowana np. jako
to stała zdefiniowana np. jako
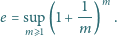
Znaleźć wszystkie funkcje
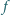 odwzorowujące zbiór liczb rzeczywistych
w siebie i spełniające dla każdych liczb rzeczywistych
odwzorowujące zbiór liczb rzeczywistych
w siebie i spełniające dla każdych liczb rzeczywistych
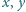 równanie
równanie
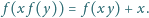 |
Rozważamy trójki liczb rzeczywistych
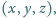 spełniające
warunki
spełniające
warunki
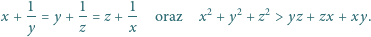 |
Wyznaczyć wszystkie możliwe wartości iloczynu
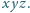
Dane są liczby rzeczywiste
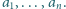 Niech
Niech
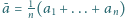 oznacza
ich średnią arytmetyczną. Udowodnić, że prawdziwa jest nierówność
oznacza
ich średnią arytmetyczną. Udowodnić, że prawdziwa jest nierówność
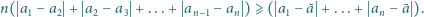 |
Udowodnić, że dowolna liczba rzeczywista
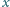 spełnia nierówność
spełnia nierówność
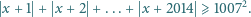 |
Rozpatrujemy takie ciągi
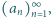 że
że
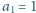 oraz, dla każdego
oraz, dla każdego
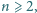
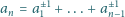
dla pewnego wyboru znaków
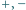 w wykładnikach. Znaleźć
najmniejszą możliwą wartość
w wykładnikach. Znaleźć
najmniejszą możliwą wartość
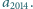
Zadanie 674 zaproponował pan Paweł Najman z Krakowa.
Znaleźć wszystkie funkcje
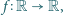 które spełniają układ równań
funkcyjnych
które spełniają układ równań
funkcyjnych
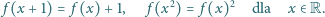
Zadanie ZM-1407 pochodzi z blogu T. Tao, http://terrytao.wordpress.com/.
Jaś, będąc na lotnisku, chce jak najszybciej przejść od punktu
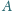 do
punktu
do
punktu
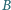 (w linii prostej). Idzie z prędkością
(w linii prostej). Idzie z prędkością
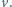 Na swojej
trasie ma odcinek, który pokonuje na ruchomej taśmie poruszającej się
z prędkością
Na swojej
trasie ma odcinek, który pokonuje na ruchomej taśmie poruszającej się
z prędkością
 (czyli Jaś, idąc po taśmie, porusza się z prędkością
(czyli Jaś, idąc po taśmie, porusza się z prędkością
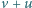 względem ziemi). Jaś ma jednak pewien zapas sił i może przez
czas
względem ziemi). Jaś ma jednak pewien zapas sił i może przez
czas
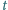 biec z prędkością
biec z prędkością
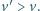 Czy powinien biec na taśmie,
czy poza nią? (Zakładamy dla uproszczenia, że taśma, jak i odcinek bez
taśmy są na tyle długie, że Jaś nie jest w stanie pokonać biegiem żadnego
z nich w całości.)
Czy powinien biec na taśmie,
czy poza nią? (Zakładamy dla uproszczenia, że taśma, jak i odcinek bez
taśmy są na tyle długie, że Jaś nie jest w stanie pokonać biegiem żadnego
z nich w całości.)
Zadanie 670 zaproponował pan Paweł Kubit z Krakowa.
Udowodnić nierówność
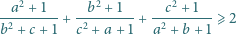
dla liczb rzeczywistych
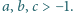
Na lotnisku Jaś chce jak najszybciej przejść z punktu
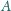 do
punktu
do
punktu
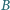 (w linii prostej). Idzie z prędkością
(w linii prostej). Idzie z prędkością
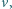 a na swojej
trasie ma odcinek, który pokonuje na ruchomej taśmie poruszającej się
z prędkością
a na swojej
trasie ma odcinek, który pokonuje na ruchomej taśmie poruszającej się
z prędkością
 (czyli idąc po taśmie, Jaś porusza się z prędkością
(czyli idąc po taśmie, Jaś porusza się z prędkością
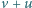 względem ziemi). Jaś musi po drodze zasznurować but, co
powoduje, że stoi przez czas
względem ziemi). Jaś musi po drodze zasznurować but, co
powoduje, że stoi przez czas
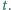 Czy powinien zasznurować but na
ruchomej taśmie, czy poza nią?
Czy powinien zasznurować but na
ruchomej taśmie, czy poza nią?
(Zakładamy dla uproszczenia, że taśma jest
na tyle długa, że Jaś zdąży zasznurować na niej but, tzn. długość taśmy
jest większa niż
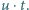 )
)
Udowodnić, że dla malejącego ciągu
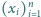 liczb rzeczywistych
dodatnich prawdziwa jest nierówność
liczb rzeczywistych
dodatnich prawdziwa jest nierówność
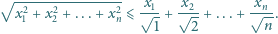 |
Udowodnić, że dla
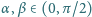 prawdziwa jest nierówność
prawdziwa jest nierówność
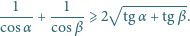 |
Kiedy zachodzi równość?
Dana jest liczba wymierna
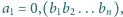 w której zapisie
dziesiętnym blok cyfr
w której zapisie
dziesiętnym blok cyfr
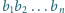 powtarza się okresowo po przecinku.
Rozważmy liczby
powtarza się okresowo po przecinku.
Rozważmy liczby
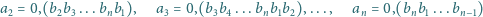
powstałe z
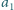 przez cykliczne przesunięcia cyfr w bloku. Udowodnić,
że
przez cykliczne przesunięcia cyfr w bloku. Udowodnić,
że
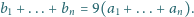
Zadanie 664 zaproponował pan Tomasz Ordowski
Dowieść, że jeśli liczba rzeczywista
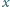 spełnia równanie
spełnia równanie
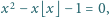 to każda potęga liczby
to każda potęga liczby
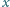 o wykładniku
dodatnim nieparzystym także spełnia to równanie.
o wykładniku
dodatnim nieparzystym także spełnia to równanie.
Udowodnić, że istnieje liczba
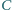 o następującej własności: jeśli
równanie
o następującej własności: jeśli
równanie
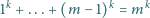
ma rozwiązanie dla pewnych liczb naturalnych
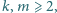 to
to
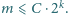
Zadanie 662 zaproponował pan Paweł Najman z Krakowa. Jest to kontynuacja zadania 654.
Ciąg
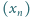 jest określony wzorem rekurencyjnym
jest określony wzorem rekurencyjnym
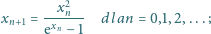
wyraz początkowy
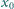 jest dowolną liczbą dodatnią. Obliczyć
granicę
jest dowolną liczbą dodatnią. Obliczyć
granicę
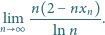
Udowodnić, że dla liczb rzeczywistych
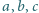 jest spełniona
nierówność
jest spełniona
nierówność
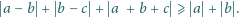
Rozstrzygnij, ile rozwiązań ma układ równań

Rozstrzygnij, ile rozwiązań ma układ równań

Niech funkcja
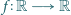 będzie ograniczona z góry, tzn. istnieje taka
liczba
będzie ograniczona z góry, tzn. istnieje taka
liczba
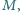 że
że
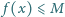 dla każdego
dla każdego
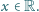 Udowodnić,
że jeśli dla wszystkich liczb rzeczywistych
Udowodnić,
że jeśli dla wszystkich liczb rzeczywistych
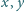 spełniona jest
nierówność
spełniona jest
nierówność
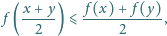
to
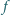 jest funkcją stałą.
jest funkcją stałą.
W szczególności, funkcje wypukłe nie są ograniczone z góry, chyba że są stałe.
Wykazać, że jeśli każda z liczb
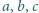 jest nie mniejsza od
jest nie mniejsza od
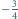 oraz
oraz
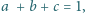 to
to

Zadanie 506 z Klubu 44M
Udowodnić, że dla dowolnych liczb dodatnich
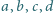 zachodzi
nierówność
zachodzi
nierówność

Udowodnić, że dla dowolnych liczb dodatnich
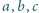 zachodzi
nierówność
zachodzi
nierówność

Zwardoń 2006
Liczby rzeczywiste
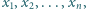 gdzie
gdzie
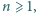 spełniają warunki
spełniają warunki

Udowodnić, że
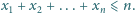
Jugosławia 1986
Udowodnić, że dla dowolnych liczb dodatnich
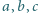 zachodzi
nierówność
zachodzi
nierówność

Japonia 1997
Udowodnić, że dla dowolnych liczb dodatnich
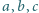 zachodzi
nierówność
zachodzi
nierówność

Zadanie 654 zaproponował pan Paweł Najman z Krakowa. Będzie ono miało dalszy ciąg w numerze 5/2013.
Ciąg
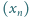 jest określony wzorem rekurencyjnym
jest określony wzorem rekurencyjnym

wyraz początkowy
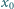 jest dowolną liczbą dodatnią. Obliczyć granicę
jest dowolną liczbą dodatnią. Obliczyć granicę
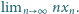
Zadanie 652 zaproponował pan Witold Bednarek z Łodzi.
Udowodnić nierówność
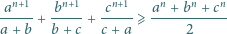
dla liczb rzeczywistych
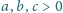 oraz liczb całkowitych
oraz liczb całkowitych
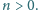
Liczby rzeczywiste
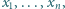 które są nie mniejsze niż
które są nie mniejsze niż
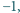 spełniają
równość
spełniają
równość
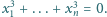 Udowodnić, że
Udowodnić, że
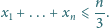
Zadanie 646 zaproponował pan Paweł Najman z Krakowa.
Niech
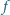 będzie funkcją o wartościach rzeczywistych, określoną na
zbiorze liczb dodatnich, dwukrotnie różniczkowalną, spełniającą warunek
będzie funkcją o wartościach rzeczywistych, określoną na
zbiorze liczb dodatnich, dwukrotnie różniczkowalną, spełniającą warunek
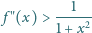 dla
dla
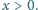 Czy taka funkcja może mieć asymptotę
przy
Czy taka funkcja może mieć asymptotę
przy