Klub 44M - zadania X 2017»Zadanie 747
o zadaniu...
- Zadanie pochodzi z artykułu Klub 44M - zadania X 2017
- Publikacja w Delcie: październik 2017
- Publikacja elektroniczna: 29 września 2017
- Artykuł źródłowy w wersji do druku [application/pdf]: (58 KB)
Funkcja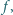 
o wartościach rzeczywistych, jest określona, wypukła i różniczkowalna na zbiorze wszystkich liczb dodatnich; przy tym 
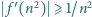dla 
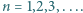Udowodnić, że funkcja 
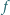jest nieograniczona.
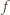wynika, że dla każdej pary liczb dodatnich 
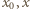zachodzi nierówność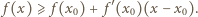
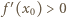w jakimkolwiek punkcie 
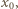to prawa strona (1) przedstawia funkcję nieograniczoną z góry i mamy tezę.
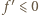(na całym przedziale 
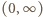). Warunek dany w założeniach mówi więc, że dla każdej liczby całkowitej 
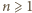mamy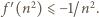 
W nierówności (1) podstawiamy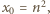 
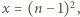i otrzymujemy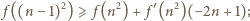
:
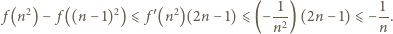
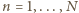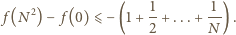
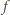jest (w rozważanym przypadku) nieograniczona z dołu.