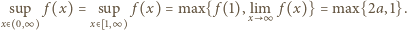Gdy 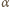 przebiega przedział
przebiega przedział 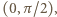 wartość
wartość 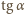 przebiega zbiór wszystkich liczb dodatnich. Należy więc znaleźć kres górny funkcji
przebiega zbiór wszystkich liczb dodatnich. Należy więc znaleźć kres górny funkcji 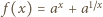 zmiennej
zmiennej 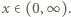 Ponieważ
Ponieważ 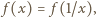 kres górny na przedziale
kres górny na przedziale 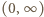 jest taki sam, jak na przedziale
jest taki sam, jak na przedziale 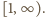 Pochodna funkcji
Pochodna funkcji 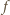 ma po prostym przekształceniu postać
ma po prostym przekształceniu postać
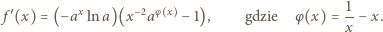
Skoro 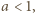 czynnik w pierwszym nawiasie jest stale dodatni. Czynnik w drugim nawiasie ma taki sam znak jak wyrażenie
czynnik w pierwszym nawiasie jest stale dodatni. Czynnik w drugim nawiasie ma taki sam znak jak wyrażenie
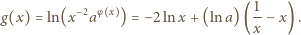
Teraz badamy funkcję 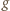 w przedziale
w przedziale 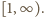 Jej pochodna:
Jej pochodna:
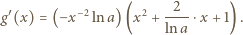
I znów, czynnik w pierwszym nawiasie jest dodatni. W drugim nawiasie widzimy trójmian kwadratowy, którego pierwiastki (rzeczywiste lub nie) mają iloczyn równy 1; w przedziale 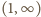 może być co najwyżej jeden pierwiastek. Dla dużych
może być co najwyżej jeden pierwiastek. Dla dużych 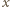 trójmian ma wartości dodatnie. Zatem wartości
trójmian ma wartości dodatnie. Zatem wartości 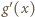 albo są dodatnie w całym przedziale
albo są dodatnie w całym przedziale 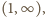 albo są - przedziałami - najpierw ujemne, potem dodatnie. Funkcja
albo są - przedziałami - najpierw ujemne, potem dodatnie. Funkcja 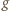 jest więc albo rosnąca, albo (kolejno) malejąca-rosnąca. A ponieważ
jest więc albo rosnąca, albo (kolejno) malejąca-rosnąca. A ponieważ 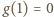 oraz
oraz 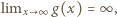 wynika stąd, że także wartości
wynika stąd, że także wartości 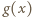 są albo stale dodatnie, albo (przedziałami, od lewej) ujemne-dodatnie.
są albo stale dodatnie, albo (przedziałami, od lewej) ujemne-dodatnie.
Funkcja 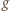 ma taki znak, jak
ma taki znak, jak 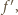 wobec czego możemy powtórzyć rozumowanie: funkcja
wobec czego możemy powtórzyć rozumowanie: funkcja 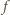 jest albo rosnąca, albo (kolejno) malejąca-rosnąca. W każdym przypadku jej kresem górnym na przedziale
jest albo rosnąca, albo (kolejno) malejąca-rosnąca. W każdym przypadku jej kresem górnym na przedziale 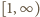 jest jej wartość lub granica w jednym z końców przedziału. Otrzymujemy wynik:
jest jej wartość lub granica w jednym z końców przedziału. Otrzymujemy wynik:
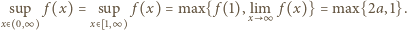
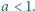 Obliczyć kres górny zbioru wartości wyrażenia
Obliczyć kres górny zbioru wartości wyrażenia 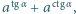 gdy zmienna
gdy zmienna 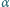 przebiega przedział
przebiega przedział 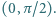

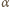 przebiega przedział
przebiega przedział 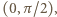 wartość
wartość 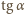 przebiega zbiór wszystkich liczb dodatnich. Należy więc znaleźć kres górny funkcji
przebiega zbiór wszystkich liczb dodatnich. Należy więc znaleźć kres górny funkcji 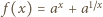 zmiennej
zmiennej 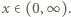 Ponieważ
Ponieważ 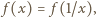 kres górny na przedziale
kres górny na przedziale 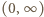 jest taki sam, jak na przedziale
jest taki sam, jak na przedziale 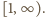 Pochodna funkcji
Pochodna funkcji 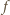 ma po prostym przekształceniu postać
ma po prostym przekształceniu postać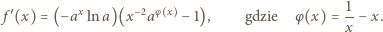
 czynnik w pierwszym nawiasie jest stale dodatni. Czynnik w drugim nawiasie ma taki sam znak jak wyrażenie
czynnik w pierwszym nawiasie jest stale dodatni. Czynnik w drugim nawiasie ma taki sam znak jak wyrażenie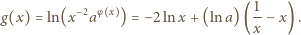
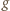 w przedziale
w przedziale 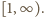 Jej pochodna:
Jej pochodna: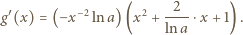
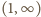 może być co najwyżej jeden pierwiastek. Dla dużych
może być co najwyżej jeden pierwiastek. Dla dużych 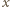 trójmian ma wartości dodatnie. Zatem wartości
trójmian ma wartości dodatnie. Zatem wartości 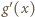 albo są dodatnie w całym przedziale
albo są dodatnie w całym przedziale 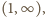 albo są - przedziałami - najpierw ujemne, potem dodatnie. Funkcja
albo są - przedziałami - najpierw ujemne, potem dodatnie. Funkcja 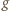 jest więc albo rosnąca, albo (kolejno) malejąca-rosnąca. A ponieważ
jest więc albo rosnąca, albo (kolejno) malejąca-rosnąca. A ponieważ 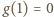 oraz
oraz 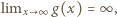 wynika stąd, że także wartości
wynika stąd, że także wartości 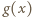 są albo stale dodatnie, albo (przedziałami, od lewej) ujemne-dodatnie.
są albo stale dodatnie, albo (przedziałami, od lewej) ujemne-dodatnie.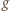 ma taki znak, jak
ma taki znak, jak 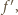 wobec czego możemy powtórzyć rozumowanie: funkcja
wobec czego możemy powtórzyć rozumowanie: funkcja 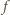 jest albo rosnąca, albo (kolejno) malejąca-rosnąca. W każdym przypadku jej kresem górnym na przedziale
jest albo rosnąca, albo (kolejno) malejąca-rosnąca. W każdym przypadku jej kresem górnym na przedziale 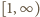 jest jej wartość lub granica w jednym z końców przedziału. Otrzymujemy wynik:
jest jej wartość lub granica w jednym z końców przedziału. Otrzymujemy wynik: