Klub 44M - zadania IV 2017»Zadanie 739
o zadaniu...
- Zadanie pochodzi z artykułu Klub 44M - zadania IV 2017
- Publikacja w Delcie: kwiecień 2017
- Publikacja elektroniczna: 30 marca 2017
- Artykuł źródłowy w wersji do druku [application/pdf]: (71 KB)
Znaleźć wszystkie funkcje 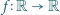 o następujących własnościach:
o następujących własnościach:
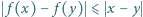 dla
dla 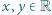 ;
;- dla każdej liczby
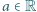 ciąg
ciąg 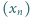 określony wzorami
określony wzorami 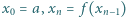 (dla
(dla 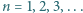 ) jest ciągiem arytmetycznym.
) jest ciągiem arytmetycznym.

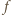 będzie funkcją, spełniającą postawione warunki, i przyjmijmy, że funkcja
będzie funkcją, spełniającą postawione warunki, i przyjmijmy, że funkcja 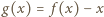 nie jest stała. Istnieją więc liczby
nie jest stała. Istnieją więc liczby 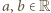 dla których
dla których 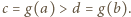 W drugim z warunków, podanych w zadaniu, przyjmujemy
W drugim z warunków, podanych w zadaniu, przyjmujemy 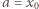 i tworzymy ciąg arytmetyczny
i tworzymy ciąg arytmetyczny 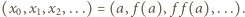 Skoro
Skoro 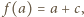 zatem
zatem 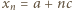 (dla wszystkich
(dla wszystkich  ). Jednocześnie
). Jednocześnie 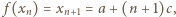 czyli
czyli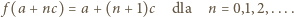
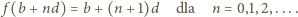
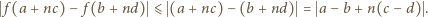
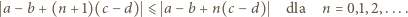
 wyrażenia ujęte w symbol wartości bezwzględnej mają wartość dodatnią (bo
wyrażenia ujęte w symbol wartości bezwzględnej mają wartość dodatnią (bo 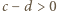 ). Można więc opuścić moduły. Ale zależność (3) - po skasowaniu modułów - redukuje się do postaci
). Można więc opuścić moduły. Ale zależność (3) - po skasowaniu modułów - redukuje się do postaci 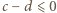 ; sprzeczność.
; sprzeczność.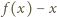 musi być stała. Jasne, że każda funkcja postaci
musi być stała. Jasne, że każda funkcja postaci 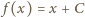 spełnia wymagane warunki.
spełnia wymagane warunki.