Klub 44M - zadania IV 2020»Zadanie 800
o zadaniu...
- Zadanie pochodzi z artykułu Klub 44M - zadania IV 2020
- Publikacja w Delcie: kwiecień 2020
- Publikacja elektroniczna: 1 kwietnia 2020
- Artykuł źródłowy w wersji do druku [application/pdf]: (404 KB)
-
Zadanie 800 zaproponował pan Michał Adamaszek z Kopenhagi.
Dla ustalonych liczb dodatnich 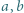 określamy funkcję
określamy funkcję 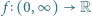 wzorem
wzorem
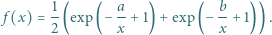 |
- Uzasadnić, że istnieje dokładnie jedna liczba
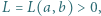 dla której
dla której 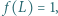 i że
i że 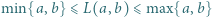 ; zatem liczba
; zatem liczba 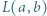 może być uważana za pewną średnią liczb
może być uważana za pewną średnią liczb 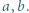
- Znaleźć, gdzie ta średnia wpisuje się w ciąg nierówności
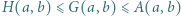 między średnimi: harmoniczną, geometryczną i arytmetyczną liczb
między średnimi: harmoniczną, geometryczną i arytmetyczną liczb 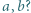

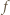 jest ciągła i rosnąca, a jej granice przy końcach dziedziny
jest ciągła i rosnąca, a jej granice przy końcach dziedziny 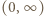 wynoszą 0 oraz
wynoszą 0 oraz 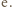 Zatem liczba
Zatem liczba 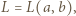 dla której
dla której 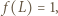 jest jednoznacznie określona. Wykażemy, że
jest jednoznacznie określona. Wykażemy, że 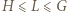 (gdzie
(gdzie 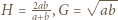 ); stąd też wyniknie, że
); stąd też wyniknie, że 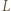 leży pomiędzy
leży pomiędzy 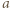 i
i 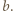 Wobec ścisłej monotoniczności funkcji
Wobec ścisłej monotoniczności funkcji 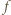 wystarczy dowieść, że
wystarczy dowieść, że 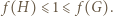
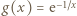 dla
dla 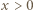 ; jest to funkcja rosnąca. Skoro
; jest to funkcja rosnąca. Skoro 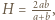 zatem
zatem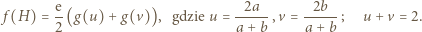
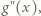 stwierdzamy, że funkcja
stwierdzamy, że funkcja 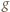 jest wklęsła w przedziale
jest wklęsła w przedziale 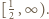 Jeżeli więc liczby
Jeżeli więc liczby 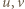 leżą w tym przedziale, to
leżą w tym przedziale, to 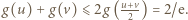 Jeśli zaś np.
Jeśli zaś np. 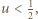 rozważamy dwa podprzypadki (pamiętając, że
rozważamy dwa podprzypadki (pamiętając, że 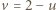 ):
):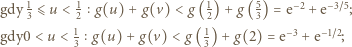
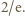 Otrzymane oszacowanie
Otrzymane oszacowanie 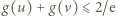 pokazuje (zgodnie ze wzorem (1)), że
pokazuje (zgodnie ze wzorem (1)), że 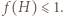
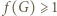 ; do tego użyjemy funkcji
; do tego użyjemy funkcji 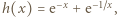 bowiem
bowiem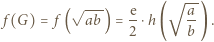
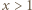 zachodzi nierówność
zachodzi nierówność 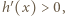 czyli
czyli 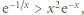 równoważna (przez logarytmowanie) nierówności
równoważna (przez logarytmowanie) nierówności 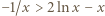 ; tę ostatnią nierówność sprawdzamy bez trudu, przenosząc wszystko na jedną stronę i ponownie różniczkując. Zatem istotnie
; tę ostatnią nierówność sprawdzamy bez trudu, przenosząc wszystko na jedną stronę i ponownie różniczkując. Zatem istotnie 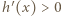 dla
dla 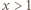 ; stąd
; stąd 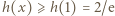 dla
dla 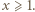 Ponieważ bez straty ogólności można przyjąć, że
Ponieważ bez straty ogólności można przyjąć, że 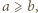 ze wzoru (2) wnosimy, że
ze wzoru (2) wnosimy, że 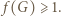 To kończy rozwiązanie.
To kończy rozwiązanie.