Ciąg 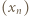 powstaje przez iterowanie funkcji
powstaje przez iterowanie funkcji 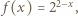 którą będziemy badać na przedziale
którą będziemy badać na przedziale ![[1,2].](/math/temat/matematyka/analiza/zadania/2018/03/25/zm-k44-759/3x-a051a26225a4472d5acd2ead6f6a678d0abff009-im-66,57,43-FF,FF,FF.gif) Ponieważ
Ponieważ 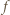 maleje od wartości
maleje od wartości 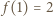 do wartości
do wartości 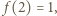 zatem odwzorowuje przedział
zatem odwzorowuje przedział ![[1,2]](/math/temat/matematyka/analiza/zadania/2018/03/25/zm-k44-759/7x-a051a26225a4472d5acd2ead6f6a678d0abff009-im-66,57,43-FF,FF,FF.gif) na siebie i ma w tym przedziale dokładnie jeden punkt stały
na siebie i ma w tym przedziale dokładnie jeden punkt stały 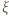 (tj. taki, że
(tj. taki, że 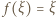 ). Obrazem przedziału
). Obrazem przedziału 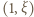 jest przedział
jest przedział 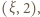 i na odwrót. Stąd wniosek, że wyrazy ciągu
i na odwrót. Stąd wniosek, że wyrazy ciągu 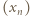 o numerach parzystych należą do jednego z tych przedziałów, a te o nieparzystych - do drugiego.
o numerach parzystych należą do jednego z tych przedziałów, a te o nieparzystych - do drugiego.
Równość 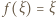 przepisujemy jako
przepisujemy jako 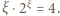 Funkcja
Funkcja 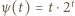 jest rosnąca; przy tym
jest rosnąca; przy tym
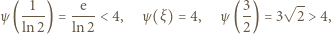
wobec czego
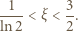 |
(1) |
Ponieważ (z założenia) 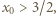 zatem
zatem 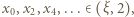 zaś
zaś 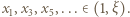
Użyjemy rachunku pochodnych. Oznaczmy (dla krótkości): 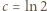 i zauważmy, że
i zauważmy, że 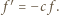 Niech
Niech 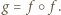 Wówczas
Wówczas
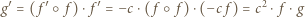
i dalej:
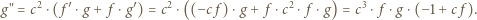 |
(2) |
Dla ![x ∈ [1,ξ]](/math/temat/matematyka/analiza/zadania/2018/03/25/zm-k44-759/1x-ebb224189cbd9ab5aa439f6248ce3382f71c3782-im-66,57,43-FF,FF,FF.gif) mamy nierówność
mamy nierówność 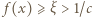 (por. (1)), więc wyrażenie w nawiasie po prawej stronie (2) ma w tych punktach wartość dodatnią. To znaczy, że funkcja
(por. (1)), więc wyrażenie w nawiasie po prawej stronie (2) ma w tych punktach wartość dodatnią. To znaczy, że funkcja 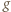 jest ściśle wypukła w przedziale
jest ściśle wypukła w przedziale ![|[1,ξ]](/math/temat/matematyka/analiza/zadania/2018/03/25/zm-k44-759/4x-ebb224189cbd9ab5aa439f6248ce3382f71c3782-im-66,57,43-FF,FF,FF.gif) ; a ponieważ
; a ponieważ 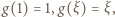 zatem
zatem
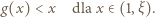 |
(3) |
Ciąg 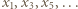 leży w przedziale
leży w przedziale 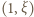 i jest generowany rekurencyjnie wzorem
i jest generowany rekurencyjnie wzorem 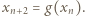 Nierówność (3) pokazuje, że jest to ciąg malejący, i w konsekwencji zbieżny. Jego granica musi być punktem stałym funkcji
Nierówność (3) pokazuje, że jest to ciąg malejący, i w konsekwencji zbieżny. Jego granica musi być punktem stałym funkcji 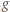 ; jednak nie ma takiego punktu w przedziale otwartym
; jednak nie ma takiego punktu w przedziale otwartym 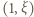 (nierówność (3)). W takim razie granicą tego ciągu musi być liczba 1.
(nierówność (3)). W takim razie granicą tego ciągu musi być liczba 1.
Funkcja ciągła 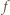 przeprowadza ten ciąg na ciąg rosnący
przeprowadza ten ciąg na ciąg rosnący 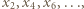 którego granicą jest wobec tego liczba
którego granicą jest wobec tego liczba 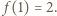 To dowodzi, że niezależnie od wyboru wyrazu początkowego
To dowodzi, że niezależnie od wyboru wyrazu początkowego 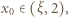 ciąg
ciąg 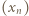 ma podciągi zbieżne do dwóch różnych granic: 1 oraz 2 (i do żadnej innej, bo dowolny podciąg ma nieskończenie wiele wspólnych wyrazów z jednym ze znalezionych podciągów, zbieżnych do 1 lub 2).
ma podciągi zbieżne do dwóch różnych granic: 1 oraz 2 (i do żadnej innej, bo dowolny podciąg ma nieskończenie wiele wspólnych wyrazów z jednym ze znalezionych podciągów, zbieżnych do 1 lub 2).
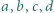 zachodzi nierówność
zachodzi nierówność
![x ,x ,...,x ∈ [−1,1] 1 2 n](/math/temat/matematyka/analiza/zadania/2019/04/29/zm-19_05-kpm-12/1x-e242253ed078688e97a06aead3aec19a78e70a97-im-2C,6B,73-FF,FF,FF.gif) spełniają warunek
spełniają warunek 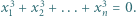 Dowieść, że
Dowieść, że
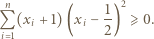
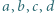 zachodzi nierówność
zachodzi nierówność

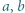 spełniają równość
spełniają równość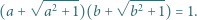
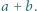
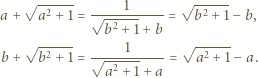
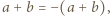 czyli
czyli 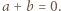
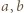 spełniające założenia zadania rzeczywiście istnieją (np.
spełniające założenia zadania rzeczywiście istnieją (np. 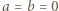 ), więc znaleziona wartość 0 istotnie jest osiągalna.
), więc znaleziona wartość 0 istotnie jest osiągalna.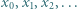 jest określony wzorami:
jest określony wzorami: 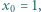

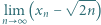 lub wykazać, że ta granica nie istnieje.
lub wykazać, że ta granica nie istnieje.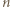 literką
literką 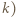 i dostajemy równoważną zależność
i dostajemy równoważną zależność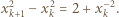
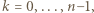 otrzymując
otrzymując
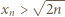 (dla
(dla 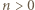 ), i wobec tego
), i wobec tego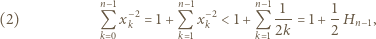
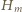 oznacza sumę odwrotności liczb naturalnych od 1 do
oznacza sumę odwrotności liczb naturalnych od 1 do  Zależności (1) i (2) dają oszacowanie
Zależności (1) i (2) dają oszacowanie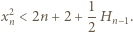
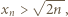 mamy stąd
mamy stąd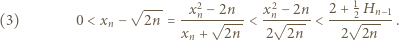
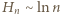 ; albo - bardziej elementarnie - z nierówności
; albo - bardziej elementarnie - z nierówności 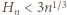 (nietrudnej do wykazania przez indukcję). Dwustronne oszacowanie (3) pokazuje, że
(nietrudnej do wykazania przez indukcję). Dwustronne oszacowanie (3) pokazuje, że 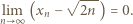
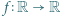 spełnia dla każdego
spełnia dla każdego 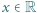 równość
równość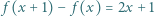
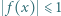 dla
dla ![x ∈[0,1].](/math/temat/matematyka/analiza/zadania/2018/12/30/zm-1588/5x-eccb368b79dc42272c83d4b8f232df0149187364-im-2C,6B,73-FF,FF,FF.gif) Wykazać, że
Wykazać, że 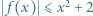 dla każdego
dla każdego 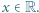
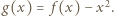 Wówczas
Wówczas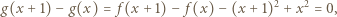
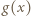 jest okresowa z okresem
jest okresowa z okresem 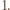 Skoro
Skoro 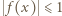 dla
dla ![|x∈ [0,1],](/math/temat/matematyka/analiza/zadania/2018/12/30/zm-1588/6x-d73afcece697591998b8c7aa137d57ff409fefb6-im-66,57,43-FF,FF,FF.gif) to
to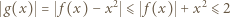
![x ∈ [0,1]](/math/temat/matematyka/analiza/zadania/2018/12/30/zm-1588/8x-d73afcece697591998b8c7aa137d57ff409fefb6-im-66,57,43-FF,FF,FF.gif) i w konsekwencji, wobec okresowości
i w konsekwencji, wobec okresowości 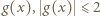 dla każdego
dla każdego 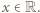 Stąd ostatecznie
Stąd ostatecznie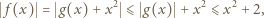
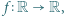 spełniające równanie
spełniające równanie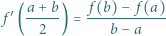
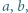 których różnica jest liczbą całkowitą.
których różnica jest liczbą całkowitą.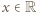 uzyskujemy z podanego równania (po podstawieniu
uzyskujemy z podanego równania (po podstawieniu 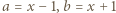 ) równość
) równość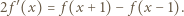
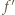 jest różniczkowalna. Możemy więc zróżniczkować (1) stronami, otrzymując
jest różniczkowalna. Możemy więc zróżniczkować (1) stronami, otrzymując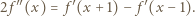
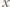 przez
przez 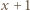 oraz
oraz 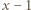 :
: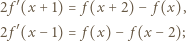
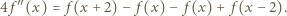
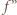 ma pochodną. Różniczkujemy (3) stronami:
ma pochodną. Różniczkujemy (3) stronami: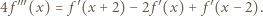
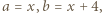 następnie
następnie 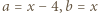 i wreszcie
i wreszcie 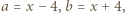 otrzymując kolejno
otrzymując kolejno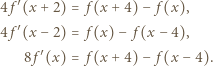
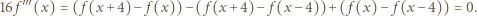
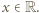 To znaczy, że
To znaczy, że 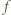 jest wielomianem stopnia najwyżej drugiego.
jest wielomianem stopnia najwyżej drugiego.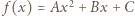 spełnia równanie dane w założeniu zadania (i to nawet dla każdej pary różnych liczb
spełnia równanie dane w założeniu zadania (i to nawet dla każdej pary różnych liczb 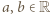 ) - co łatwo sprawdzić.
) - co łatwo sprawdzić.
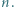
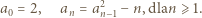
 warunek
warunek 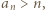 co można sprawdzić indukcyjnie: dla 1, 2 i 3 sprawdzamy bezpośrednio, ponadto jeśli
co można sprawdzić indukcyjnie: dla 1, 2 i 3 sprawdzamy bezpośrednio, ponadto jeśli 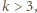 to mamy
to mamy 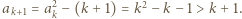 Kolejno otrzymujemy zatem
Kolejno otrzymujemy zatem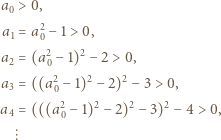
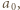 otrzymujemy kolejno
otrzymujemy kolejno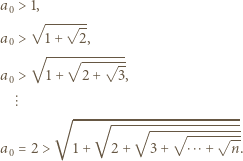
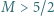 taką, że dla dowolnych liczb dodatnich
taką, że dla dowolnych liczb dodatnich 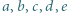 zachodzi nierówność
zachodzi nierówność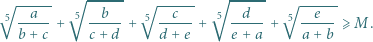
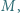 tym lepsze rozwiązanie.
tym lepsze rozwiązanie.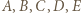 (więc
(więc 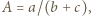 itd.). Wobec cykliczności można przyjąć, że
itd.). Wobec cykliczności można przyjąć, że 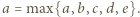 Dalej oznaczmy
Dalej oznaczmy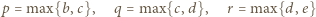
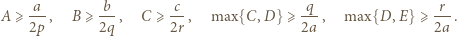
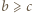 (czyli
(czyli 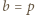 ), wówczas
), wówczas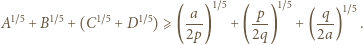
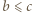 (czyli
(czyli 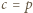 ), wówczas
), wówczas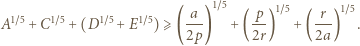
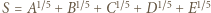 ; zaś po prawej stronie - sumę trzech liczb, których iloczyn wynosi
; zaś po prawej stronie - sumę trzech liczb, których iloczyn wynosi 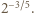 Z nierówności między średnimi dostajemy oszacowanie
Z nierówności między średnimi dostajemy oszacowanie 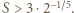 Liczba
Liczba 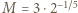 spełnia wymagany warunek
spełnia wymagany warunek 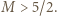
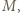 wraz z powyższym uzasadnieniem, zaproponował pan Piotr Kumor, autor zadania; kto da więcej?).
wraz z powyższym uzasadnieniem, zaproponował pan Piotr Kumor, autor zadania; kto da więcej?).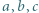 spełniają nierówność
spełniają nierówność 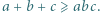 Udowodnić, że
Udowodnić, że 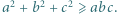
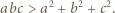
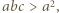 skąd
skąd 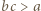 i analogicznie
i analogicznie 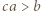 oraz
oraz 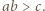 Ponadto mamy
Ponadto mamy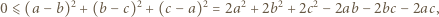
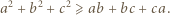
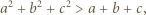
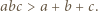
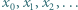 jest określony wzorem rekurencyjnym
jest określony wzorem rekurencyjnym 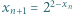 dla
dla 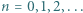 ; wyraz początkowy
; wyraz początkowy 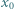 jest dowolną liczbą z przedziału
jest dowolną liczbą z przedziału 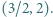 Wyznaczyć wszystkie liczby, będące granicami zbieżnych podciągów ciągu
Wyznaczyć wszystkie liczby, będące granicami zbieżnych podciągów ciągu 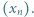
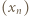 powstaje przez iterowanie funkcji
powstaje przez iterowanie funkcji 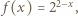 którą będziemy badać na przedziale
którą będziemy badać na przedziale ![[1,2].](/math/temat/matematyka/analiza/zadania/2018/03/25/zm-k44-759/3x-a051a26225a4472d5acd2ead6f6a678d0abff009-im-66,57,43-FF,FF,FF.gif) Ponieważ
Ponieważ 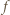 maleje od wartości
maleje od wartości 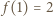 do wartości
do wartości 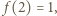 zatem odwzorowuje przedział
zatem odwzorowuje przedział ![[1,2]](/math/temat/matematyka/analiza/zadania/2018/03/25/zm-k44-759/7x-a051a26225a4472d5acd2ead6f6a678d0abff009-im-66,57,43-FF,FF,FF.gif) na siebie i ma w tym przedziale dokładnie jeden punkt stały
na siebie i ma w tym przedziale dokładnie jeden punkt stały 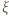 (tj. taki, że
(tj. taki, że 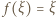 ). Obrazem przedziału
). Obrazem przedziału 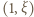 jest przedział
jest przedział 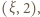 i na odwrót. Stąd wniosek, że wyrazy ciągu
i na odwrót. Stąd wniosek, że wyrazy ciągu 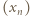 o numerach parzystych należą do jednego z tych przedziałów, a te o nieparzystych - do drugiego.
o numerach parzystych należą do jednego z tych przedziałów, a te o nieparzystych - do drugiego.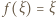 przepisujemy jako
przepisujemy jako 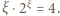 Funkcja
Funkcja 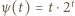 jest rosnąca; przy tym
jest rosnąca; przy tym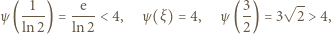
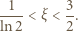
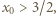 zatem
zatem 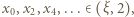 zaś
zaś 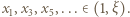
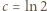 i zauważmy, że
i zauważmy, że 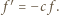 Niech
Niech 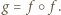 Wówczas
Wówczas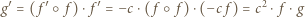
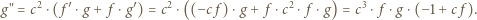
![x ∈ [1,ξ]](/math/temat/matematyka/analiza/zadania/2018/03/25/zm-k44-759/1x-ebb224189cbd9ab5aa439f6248ce3382f71c3782-im-66,57,43-FF,FF,FF.gif) mamy nierówność
mamy nierówność 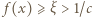 (por. (1)), więc wyrażenie w nawiasie po prawej stronie (2) ma w tych punktach wartość dodatnią. To znaczy, że funkcja
(por. (1)), więc wyrażenie w nawiasie po prawej stronie (2) ma w tych punktach wartość dodatnią. To znaczy, że funkcja 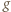 jest ściśle wypukła w przedziale
jest ściśle wypukła w przedziale ![|[1,ξ]](/math/temat/matematyka/analiza/zadania/2018/03/25/zm-k44-759/4x-ebb224189cbd9ab5aa439f6248ce3382f71c3782-im-66,57,43-FF,FF,FF.gif) ; a ponieważ
; a ponieważ 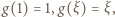 zatem
zatem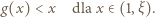
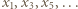 leży w przedziale
leży w przedziale 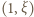 i jest generowany rekurencyjnie wzorem
i jest generowany rekurencyjnie wzorem 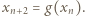 Nierówność (3) pokazuje, że jest to ciąg malejący, i w konsekwencji zbieżny. Jego granica musi być punktem stałym funkcji
Nierówność (3) pokazuje, że jest to ciąg malejący, i w konsekwencji zbieżny. Jego granica musi być punktem stałym funkcji 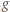 ; jednak nie ma takiego punktu w przedziale otwartym
; jednak nie ma takiego punktu w przedziale otwartym 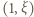 (nierówność (3)). W takim razie granicą tego ciągu musi być liczba 1.
(nierówność (3)). W takim razie granicą tego ciągu musi być liczba 1.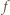 przeprowadza ten ciąg na ciąg rosnący
przeprowadza ten ciąg na ciąg rosnący 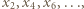 którego granicą jest wobec tego liczba
którego granicą jest wobec tego liczba 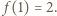 To dowodzi, że niezależnie od wyboru wyrazu początkowego
To dowodzi, że niezależnie od wyboru wyrazu początkowego 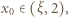 ciąg
ciąg 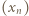 ma podciągi zbieżne do dwóch różnych granic: 1 oraz 2 (i do żadnej innej, bo dowolny podciąg ma nieskończenie wiele wspólnych wyrazów z jednym ze znalezionych podciągów, zbieżnych do 1 lub 2).
ma podciągi zbieżne do dwóch różnych granic: 1 oraz 2 (i do żadnej innej, bo dowolny podciąg ma nieskończenie wiele wspólnych wyrazów z jednym ze znalezionych podciągów, zbieżnych do 1 lub 2).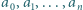 są takie, że
są takie, że 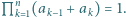 Udowodnić, że
Udowodnić, że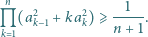
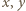 oraz dodatniej liczby całkowitej
oraz dodatniej liczby całkowitej 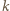 zachodzi nierówność
zachodzi nierówność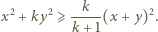
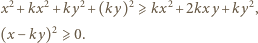
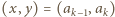 dla
dla 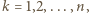 mnożąc otrzymane związki stronami i korzystając z założenia zadania, uzyskujemy
mnożąc otrzymane związki stronami i korzystając z założenia zadania, uzyskujemy 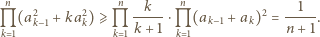
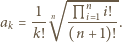
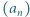 zadany przez
zadany przez 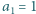 oraz
oraz 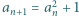 dla
dla 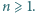 Rozstrzygnąć, czy istnieje dodatnia liczba całkowita
Rozstrzygnąć, czy istnieje dodatnia liczba całkowita 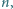 dla której
dla której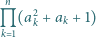
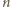 nie istnieje.
nie istnieje.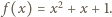 Bezpośrednio sprawdzamy, że dla dowolnego
Bezpośrednio sprawdzamy, że dla dowolnego 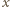 zachodzi równość
zachodzi równość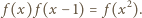
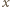 jest dodatnią liczbą całkowitą, to
jest dodatnią liczbą całkowitą, to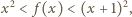
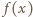 nie jest kwadratem liczby całkowitej.
nie jest kwadratem liczby całkowitej.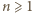 zachodzi równość
zachodzi równość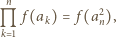
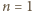 równość
równość 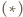 jest spełniona. Przypuśćmy, że zachodzi ona dla pewnego
jest spełniona. Przypuśćmy, że zachodzi ona dla pewnego 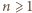 ; wówczas
; wówczas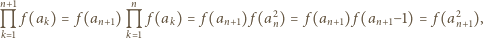
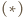 zachodzi również dla
zachodzi również dla 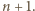 To kończy rozwiązanie.
To kończy rozwiązanie.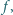 o wartościach rzeczywistych, jest określona, wypukła i różniczkowalna na zbiorze wszystkich liczb dodatnich; przy tym
o wartościach rzeczywistych, jest określona, wypukła i różniczkowalna na zbiorze wszystkich liczb dodatnich; przy tym 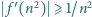 dla
dla 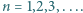 Udowodnić, że funkcja
Udowodnić, że funkcja 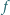 jest nieograniczona.
jest nieograniczona.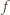 wynika, że dla każdej pary liczb dodatnich
wynika, że dla każdej pary liczb dodatnich 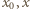 zachodzi nierówność
zachodzi nierówność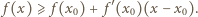
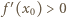 w jakimkolwiek punkcie
w jakimkolwiek punkcie 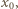 to prawa strona (1) przedstawia funkcję nieograniczoną z góry i mamy tezę.
to prawa strona (1) przedstawia funkcję nieograniczoną z góry i mamy tezę.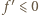 (na całym przedziale
(na całym przedziale 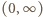 ). Warunek dany w założeniach mówi więc, że dla każdej liczby całkowitej
). Warunek dany w założeniach mówi więc, że dla każdej liczby całkowitej 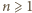 mamy
mamy 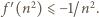 W nierówności (1) podstawiamy
W nierówności (1) podstawiamy 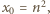
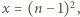 i otrzymujemy
i otrzymujemy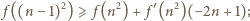
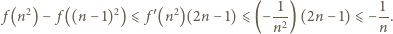
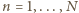 :
: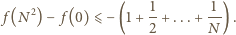
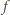 jest (w rozważanym przypadku) nieograniczona z dołu.
jest (w rozważanym przypadku) nieograniczona z dołu.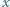 oraz dla każdej dodatniej liczby całkowitej
oraz dla każdej dodatniej liczby całkowitej 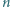 istnieje co najmniej
istnieje co najmniej 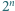 różnych wyborów znaków
różnych wyborów znaków 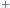 i
i  w wyrażeniu
w wyrażeniu 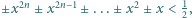 dla których ta nierówność jest spełniona.
dla których ta nierówność jest spełniona.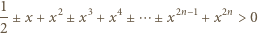
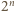 możliwych wyborów znaków. Rzeczywiście, lewą stronę powyższej nierówności można zapisać w postaci
możliwych wyborów znaków. Rzeczywiście, lewą stronę powyższej nierówności można zapisać w postaci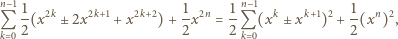
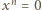 oraz
oraz 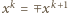 (dla
(dla 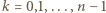 i pewnych wyborów znaków
i pewnych wyborów znaków 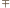 ) nie mogą wszystkie zachodzić jednocześnie.
) nie mogą wszystkie zachodzić jednocześnie.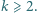 Czy istnieje rosnący ciąg liczb naturalnych
Czy istnieje rosnący ciąg liczb naturalnych 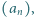 którego żaden wyraz ani żadna suma skończenie wielu jego wyrazów nie jest
którego żaden wyraz ani żadna suma skończenie wielu jego wyrazów nie jest 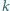 -tą potęgą liczby naturalnej, a przy tym ciąg
-tą potęgą liczby naturalnej, a przy tym ciąg 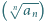 jest ograniczony?
jest ograniczony?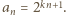
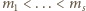 :
: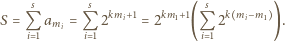
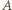 zachodziła równość
zachodziła równość 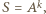 wówczas pisząc
wówczas pisząc 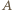 w postaci
w postaci 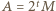 (
( 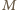 nieparzyste) i przyrównując potęgi dwójki w
nieparzyste) i przyrównując potęgi dwójki w 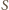 i w
i w 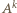 uzyskalibyśmy równość
uzyskalibyśmy równość 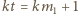 ; oczywista sprzeczność.
; oczywista sprzeczność.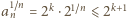 jest ograniczony.
jest ograniczony.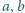 spełniają warunek
spełniają warunek 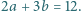 Wykazać, że dla każdej liczby naturalnej
Wykazać, że dla każdej liczby naturalnej 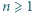 zachodzi nierówność
zachodzi nierówność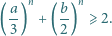
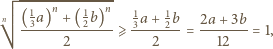
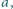 dla której zachodzi implikacja:
dla której zachodzi implikacja: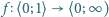 spełnia warunki
spełnia warunki 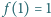 oraz
oraz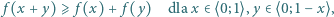
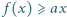 dla
dla 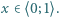
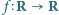 spełnia wraz z pewną funkcją
spełnia wraz z pewną funkcją 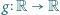 równanie
równanie 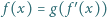 dla
dla 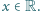 Dowieść, że funkcja
Dowieść, że funkcja 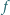 jest wypukła lub wklęsła.
jest wypukła lub wklęsła.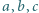 większe od
większe od 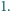 Następnie na kartce zapisano w przypadkowej kolejności cztery liczby, będące wynikami działań
Następnie na kartce zapisano w przypadkowej kolejności cztery liczby, będące wynikami działań 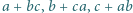 oraz
oraz 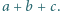 Czy znając liczby napisane na kartce można jednoznacznie określić, jakie trzy liczby znajdują się na tablicy?
Czy znając liczby napisane na kartce można jednoznacznie określić, jakie trzy liczby znajdują się na tablicy?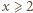 oraz
oraz 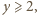 to
to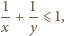
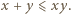 To oznacza, że
To oznacza, że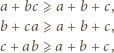
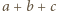 ; oznaczmy tę liczbę przez
; oznaczmy tę liczbę przez 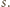 Pozostałe liczby oznaczmy przez
Pozostałe liczby oznaczmy przez 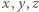 i przyjmijmy (bez straty ogólności, z uwagi na symetrię ról liczb z tablicy), że
i przyjmijmy (bez straty ogólności, z uwagi na symetrię ról liczb z tablicy), że 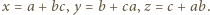 Wówczas
Wówczas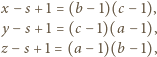
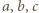 są większe od
są większe od 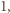 to
to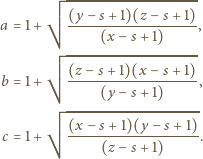
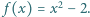 Udowodnić, że dla każdego
Udowodnić, że dla każdego 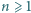 równanie
równanie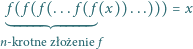
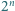 różnych rozwiązań rzeczywistych.
różnych rozwiązań rzeczywistych.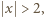 to
to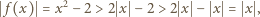
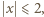 a zatem
a zatem 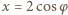 dla pewnego (a właściwie dwóch)
dla pewnego (a właściwie dwóch) ![|φ ∈[0,π].](/math/temat/matematyka/analiza/zadania/2017/03/28/zm-1526/5x-94d4870f08a4a7df010ba0743063b7dc565988e4-im-66,57,43-FF,FF,FF.gif)
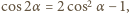 to
to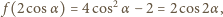
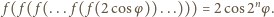
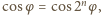 czyli
czyli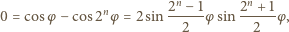
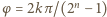 lub
lub 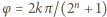 dla pewnej liczby całkowitej
dla pewnej liczby całkowitej 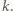 Pozostaje zauważyć, że jeżeli
Pozostaje zauważyć, że jeżeli 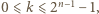 to
to 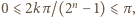 jeżeli zaś
jeżeli zaś 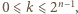 to
to 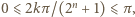 przy czym rozwiązania są różne, o ile tylko
przy czym rozwiązania są różne, o ile tylko 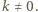 Tym samym otrzymujemy łącznie
Tym samym otrzymujemy łącznie 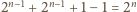 różnych rozwiązań postaci
różnych rozwiązań postaci 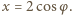
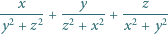
 mogą być dowolnymi liczbami dodatnimi, spełniającymi warunek
mogą być dowolnymi liczbami dodatnimi, spełniającymi warunek 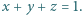
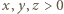 o sumie równej 1. Funkcja
o sumie równej 1. Funkcja 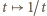 jest wypukła w przedziale
jest wypukła w przedziale 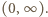 Stosujemy do niej nierówność Jensena dla trójki punktów
Stosujemy do niej nierówność Jensena dla trójki punktów 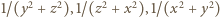 z wagami
z wagami 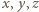 :
: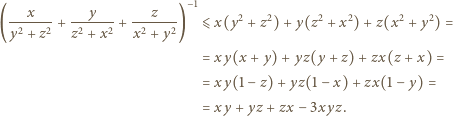
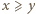 oraz
oraz 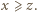 Wówczas
Wówczas 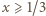 oraz
oraz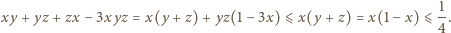
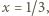 zaś druga - tylko dla
zaś druga - tylko dla 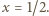 Stąd wniosek, że
Stąd wniosek, że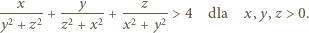
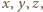 wśród których jedna jest zerem, rozważana suma nadal miałaby sens oraz przyjęłaby wartość 4 dla
wśród których jedna jest zerem, rozważana suma nadal miałaby sens oraz przyjęłaby wartość 4 dla 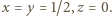 Przy założeniu, że
Przy założeniu, że 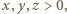 wartość 4 jest (jak widać) nieosiągalna; ale jest granicą badanej sumy np. dla
wartość 4 jest (jak widać) nieosiągalna; ale jest granicą badanej sumy np. dla 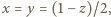 gdy
gdy 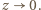 Jest więc jej kresem dolnym.
Jest więc jej kresem dolnym.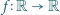 o następujących własnościach:
o następujących własnościach: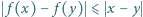 dla
dla 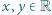 ;
;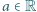 ciąg
ciąg 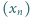 określony wzorami
określony wzorami 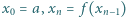 (dla
(dla 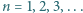 ) jest ciągiem arytmetycznym.
) jest ciągiem arytmetycznym.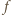 będzie funkcją, spełniającą postawione warunki, i przyjmijmy, że funkcja
będzie funkcją, spełniającą postawione warunki, i przyjmijmy, że funkcja 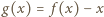 nie jest stała. Istnieją więc liczby
nie jest stała. Istnieją więc liczby 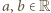 dla których
dla których 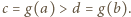 W drugim z warunków, podanych w zadaniu, przyjmujemy
W drugim z warunków, podanych w zadaniu, przyjmujemy 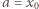 i tworzymy ciąg arytmetyczny
i tworzymy ciąg arytmetyczny 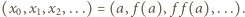 Skoro
Skoro 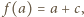 zatem
zatem 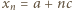 (dla wszystkich
(dla wszystkich  ). Jednocześnie
). Jednocześnie 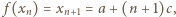 czyli
czyli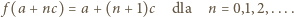
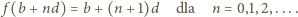
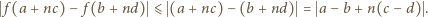
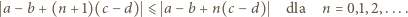
 wyrażenia ujęte w symbol wartości bezwzględnej mają wartość dodatnią (bo
wyrażenia ujęte w symbol wartości bezwzględnej mają wartość dodatnią (bo 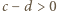 ). Można więc opuścić moduły. Ale zależność (3) - po skasowaniu modułów - redukuje się do postaci
). Można więc opuścić moduły. Ale zależność (3) - po skasowaniu modułów - redukuje się do postaci 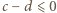 ; sprzeczność.
; sprzeczność.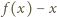 musi być stała. Jasne, że każda funkcja postaci
musi być stała. Jasne, że każda funkcja postaci 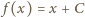 spełnia wymagane warunki.
spełnia wymagane warunki.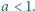 Obliczyć kres górny zbioru wartości wyrażenia
Obliczyć kres górny zbioru wartości wyrażenia 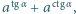 gdy zmienna
gdy zmienna 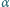 przebiega przedział
przebiega przedział 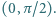
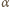 przebiega przedział
przebiega przedział 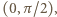 wartość
wartość 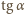 przebiega zbiór wszystkich liczb dodatnich. Należy więc znaleźć kres górny funkcji
przebiega zbiór wszystkich liczb dodatnich. Należy więc znaleźć kres górny funkcji 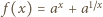 zmiennej
zmiennej 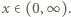 Ponieważ
Ponieważ 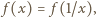 kres górny na przedziale
kres górny na przedziale 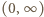 jest taki sam, jak na przedziale
jest taki sam, jak na przedziale 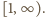 Pochodna funkcji
Pochodna funkcji 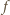 ma po prostym przekształceniu postać
ma po prostym przekształceniu postać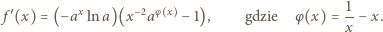
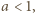 czynnik w pierwszym nawiasie jest stale dodatni. Czynnik w drugim nawiasie ma taki sam znak jak wyrażenie
czynnik w pierwszym nawiasie jest stale dodatni. Czynnik w drugim nawiasie ma taki sam znak jak wyrażenie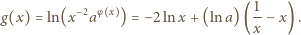
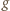 w przedziale
w przedziale 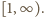 Jej pochodna:
Jej pochodna: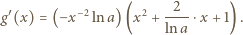
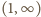 może być co najwyżej jeden pierwiastek. Dla dużych
może być co najwyżej jeden pierwiastek. Dla dużych 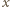 trójmian ma wartości dodatnie. Zatem wartości
trójmian ma wartości dodatnie. Zatem wartości 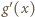 albo są dodatnie w całym przedziale
albo są dodatnie w całym przedziale 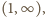 albo są - przedziałami - najpierw ujemne, potem dodatnie. Funkcja
albo są - przedziałami - najpierw ujemne, potem dodatnie. Funkcja 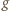 jest więc albo rosnąca, albo (kolejno) malejąca-rosnąca. A ponieważ
jest więc albo rosnąca, albo (kolejno) malejąca-rosnąca. A ponieważ 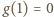 oraz
oraz 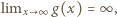 wynika stąd, że także wartości
wynika stąd, że także wartości 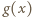 są albo stale dodatnie, albo (przedziałami, od lewej) ujemne-dodatnie.
są albo stale dodatnie, albo (przedziałami, od lewej) ujemne-dodatnie.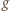 ma taki znak, jak
ma taki znak, jak 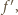 wobec czego możemy powtórzyć rozumowanie: funkcja
wobec czego możemy powtórzyć rozumowanie: funkcja 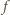 jest albo rosnąca, albo (kolejno) malejąca-rosnąca. W każdym przypadku jej kresem górnym na przedziale
jest albo rosnąca, albo (kolejno) malejąca-rosnąca. W każdym przypadku jej kresem górnym na przedziale 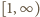 jest jej wartość lub granica w jednym z końców przedziału. Otrzymujemy wynik:
jest jej wartość lub granica w jednym z końców przedziału. Otrzymujemy wynik: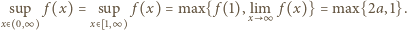
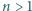 oraz dla dowolnych liczb rzeczywistych dodatnich
oraz dla dowolnych liczb rzeczywistych dodatnich 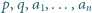 zachodzi nierówność
zachodzi nierówność
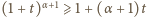 (słusznej dla
(słusznej dla 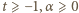 ) wykonujemy "przesunięcie zmiennej"
) wykonujemy "przesunięcie zmiennej" 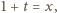 uzyskując postać
uzyskując postać
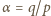 oraz
oraz 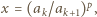 dostajemy
dostajemy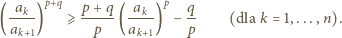
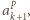 otrzymując
otrzymując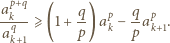
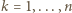 ) to teza zadania.
) to teza zadania.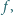 określone na zbiorze wszystkich liczb rzeczywistych różnych od zera, przyjmujące wartości w tym samym zbiorze, i spełniające równanie funkcyjne
określone na zbiorze wszystkich liczb rzeczywistych różnych od zera, przyjmujące wartości w tym samym zbiorze, i spełniające równanie funkcyjne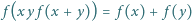
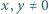 takiej, że
takiej, że 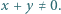
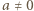 i przyjmijmy
i przyjmijmy 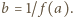 Załóżmy, że
Załóżmy, że 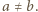 Możemy wówczas podstawić w podanym równaniu
Możemy wówczas podstawić w podanym równaniu 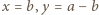 (bo
(bo 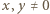 ), otrzymując związek
), otrzymując związek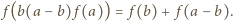
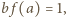 więc liczba po lewej stronie jest równa
więc liczba po lewej stronie jest równa 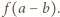 Prawa strona ma inną wartość, skoro
Prawa strona ma inną wartość, skoro 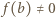 (wartości funkcji
(wartości funkcji 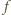 są z założenia niezerowe). Sprzeczność dowodzi, że
są z założenia niezerowe). Sprzeczność dowodzi, że 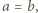 czyli
czyli 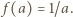 Wobec dowolności liczby
Wobec dowolności liczby 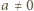 znaczy to, że funkcja
znaczy to, że funkcja 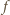 jest dana wzorem
jest dana wzorem 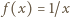 dla wszystkich
dla wszystkich 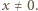 Sprawdzenie, że ta funkcja spełnia zadane równanie, jest natychmiastowe. Jest ona zatem jedynym rozwiązaniem tego równania.
Sprawdzenie, że ta funkcja spełnia zadane równanie, jest natychmiastowe. Jest ona zatem jedynym rozwiązaniem tego równania.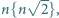 gdy
gdy 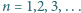
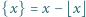 ).
).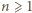 i oznaczmy
i oznaczmy 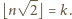 Oczywiście
Oczywiście 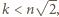 czyli
czyli 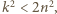 zatem
zatem 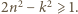 Dostajemy oszacowanie
Dostajemy oszacowanie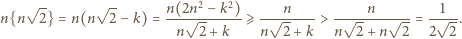
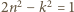 ; druga będzie "bliska równości", gdy stosunek
; druga będzie "bliska równości", gdy stosunek 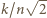 będzie bliski 1.
będzie bliski 1.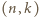 równania
równania 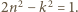 Para
Para 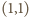 jest rozwiązaniem. Dalej, jeśli para
jest rozwiązaniem. Dalej, jeśli para 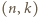 jest rozwiązaniem, to
jest rozwiązaniem, to 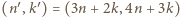 też, bowiem
też, bowiem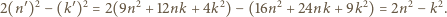
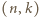 z dowolnie wielką wartością
z dowolnie wielką wartością 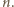 Gdy
Gdy 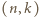 jest dowolną z takich par, wówczas
jest dowolną z takich par, wówczas 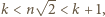 czyli
czyli 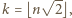 wobec czego (zgodnie z początkowym przekształceniem)
wobec czego (zgodnie z początkowym przekształceniem)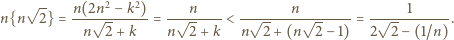
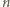 może być dowolnie wielka, zatem ostatnie wyrażenie może mieć wartość dowolnie bliską
może być dowolnie wielka, zatem ostatnie wyrażenie może mieć wartość dowolnie bliską 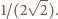 To dowodzi, że istotnie liczba
To dowodzi, że istotnie liczba 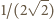 jest kresem dolnym zbioru wartości
jest kresem dolnym zbioru wartości 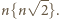
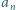 spełnia warunek
spełnia warunek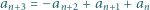
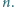 Znaleźć wartość
Znaleźć wartość 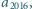 wiedząc, że
wiedząc, że 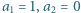 i
i 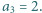
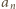 spełnia warunek
spełnia warunek 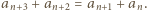 W takim razie
W takim razie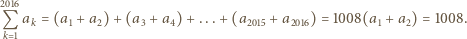
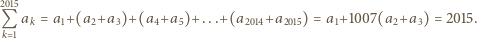
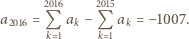
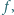 będąca różnowartościowym odwzorowaniem zbioru wszystkich liczb dodatnich na ten sam zbiór, i taka, że jej pochodna jest funkcją odwrotną do
będąca różnowartościowym odwzorowaniem zbioru wszystkich liczb dodatnich na ten sam zbiór, i taka, że jej pochodna jest funkcją odwrotną do 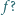
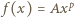 (motywacja: zarówno pochodna, jak i funkcja odwrotna do takiej funkcji, też ma taką postać - próba ma szansę powodzenia). Gdy stałe
(motywacja: zarówno pochodna, jak i funkcja odwrotna do takiej funkcji, też ma taką postać - próba ma szansę powodzenia). Gdy stałe 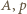 są dodatnie, funkcja
są dodatnie, funkcja 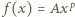 jest ściśle rosnąca i przekształca przedział
jest ściśle rosnąca i przekształca przedział 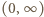 na ten sam przedział. Dla ustalonej wartości
na ten sam przedział. Dla ustalonej wartości 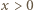 rozwiązujemy równanie
rozwiązujemy równanie 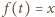 (z niewiadomą
(z niewiadomą 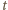 ), otrzymując
), otrzymując 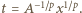 Tak więc
Tak więc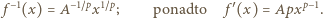
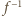 i
i 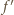 były identyczne, wystarczy, by parametry dodatnie
były identyczne, wystarczy, by parametry dodatnie 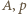 spełniały równania
spełniały równania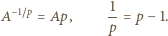
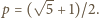 Dla tej stałej
Dla tej stałej 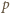 pierwsze równanie przybiera formę
pierwsze równanie przybiera formę 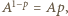 z rozwiązaniem
z rozwiązaniem 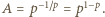 Funkcja
Funkcja 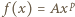 z tymi parametrami ma wymaganą własność.
z tymi parametrami ma wymaganą własność.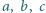 spełniają równanie
spełniają równanie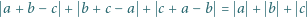
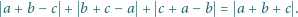
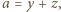
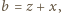
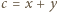 przeprowadza dane dwa równania do postaci
przeprowadza dane dwa równania do postaci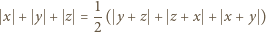
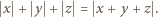
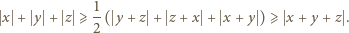
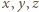 spełniają równanie (2), to spełniają też i równanie (1). Pozostaje do wykazania implikacja przeciwna.
spełniają równanie (2), to spełniają też i równanie (1). Pozostaje do wykazania implikacja przeciwna.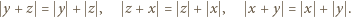
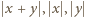 są długościami boków trójkąta (na płaszczyźnie zespolonej) o wierzchołkach
są długościami boków trójkąta (na płaszczyźnie zespolonej) o wierzchołkach 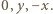 Równość
Równość 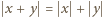 oznacza, że jest on zdegenerowany do odcinka o końcach
oznacza, że jest on zdegenerowany do odcinka o końcach 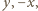 czyli że punkty
czyli że punkty 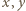 leżą na jednej półprostej, wychodzącej z punktu
leżą na jednej półprostej, wychodzącej z punktu 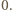 Ta sama konkluzja dla par
Ta sama konkluzja dla par 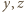 oraz
oraz 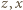 pokazuje, że wszystkie trzy punk
pokazuje, że wszystkie trzy punk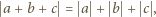
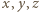 ) równaniu, łączącemu prawe strony (1) i (2). Prosty przykład:
) równaniu, łączącemu prawe strony (1) i (2). Prosty przykład: 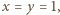
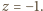 Równania (1) i (2) nie są spełnione, ale ich prawe strony mają jednakową wartość.
Równania (1) i (2) nie są spełnione, ale ich prawe strony mają jednakową wartość.