Klub 44M - zadania XII 2016»Zadanie 731
o zadaniu...
- Zadanie pochodzi z artykułu Klub 44M - zadania XII 2016
- Publikacja w Delcie: grudzień 2016
- Publikacja elektroniczna: 30 listopada 2016
- Artykuł źródłowy w wersji do druku [application/pdf]: (79 KB)
Znaleźć wszystkie funkcje 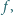 określone na zbiorze wszystkich liczb rzeczywistych różnych od zera, przyjmujące wartości w tym samym zbiorze, i spełniające równanie funkcyjne
określone na zbiorze wszystkich liczb rzeczywistych różnych od zera, przyjmujące wartości w tym samym zbiorze, i spełniające równanie funkcyjne
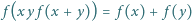
dla każdej pary liczb 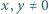 takiej, że
takiej, że 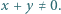

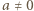 i przyjmijmy
i przyjmijmy 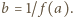 Załóżmy, że
Załóżmy, że 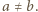 Możemy wówczas podstawić w podanym równaniu
Możemy wówczas podstawić w podanym równaniu 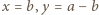 (bo
(bo 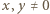 ), otrzymując związek
), otrzymując związek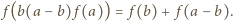
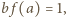 więc liczba po lewej stronie jest równa
więc liczba po lewej stronie jest równa 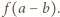 Prawa strona ma inną wartość, skoro
Prawa strona ma inną wartość, skoro 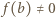 (wartości funkcji
(wartości funkcji 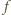 są z założenia niezerowe). Sprzeczność dowodzi, że
są z założenia niezerowe). Sprzeczność dowodzi, że 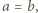 czyli
czyli 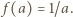 Wobec dowolności liczby
Wobec dowolności liczby 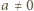 znaczy to, że funkcja
znaczy to, że funkcja 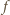 jest dana wzorem
jest dana wzorem 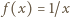 dla wszystkich
dla wszystkich 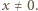 Sprawdzenie, że ta funkcja spełnia zadane równanie, jest natychmiastowe. Jest ona zatem jedynym rozwiązaniem tego równania.
Sprawdzenie, że ta funkcja spełnia zadane równanie, jest natychmiastowe. Jest ona zatem jedynym rozwiązaniem tego równania.