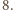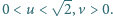
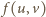Zauważmy najpierw, że to kwadrat odległości między punktami 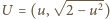oraz

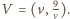
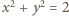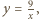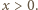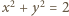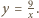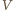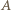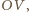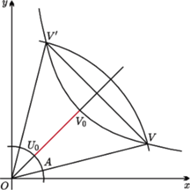
Pierwszy punkt leży na okręgu zadanym równaniem (a dokładniej na jego części znajdującej się w pierwszej ćwiartce układu współrzędnych), a drugi na gałęzi hiperboli dla Aby znaleźć najmniejszą wartość funkcji wystarczy znaleźć odległość okręgu od hiperboli Niech będzie wybranym punktem na hiperboli, a punkt punktem przecięcia z odcinkiem gdzie 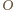jest środkiem układu współrzędnych (patrz rysunek). Odległość punktu 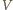od jest równa długości odcinka 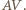Niech punkt 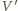będzie symetryczny do 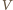względem prostej 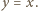Odległość 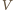od jest równa odległości 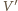od 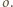Ponadto, z wypukłości funkcji 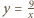dla 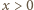wynika, że punkt 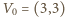znajduje się po przeciwnej stronie prostej niż łuk okręgu o środku w punkcie 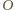i promieniu równym długości odcinka 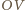łączący punkty 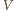i 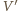(patrz rysunek). 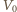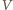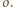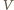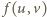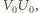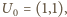Zatem odległość od jest mniejsza niż odległość od Z dowolności wynika, że najmniejsza wartość funkcji jest równa kwadratowi długości odcinka gdzie czyli